最短路径生成树计数。
我们应该先明白什么是最短路径生成树,不会戳这里。
计数方法明显是要使用乘法原理计数,也就是说我们可以得出每一步的方案数再乘进答案中。
接下来考虑如何的出每一步的方案数,所谓方案数也就是对于每一个D[i]D[i]D[i]可以从多少个D[j]D[j]D[j]转移过来,那么显然,比较大的距离只能从比较小的距离转移过来。
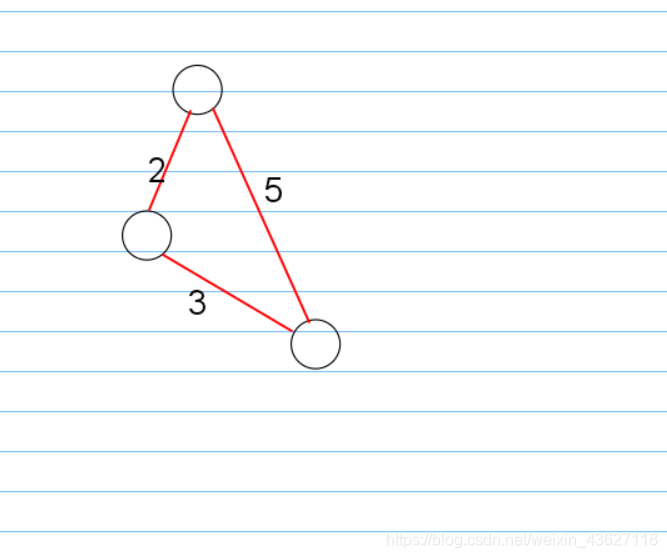
所以我们可以先给DDD数组递增排序。 这样比iii小的都是有可能转移到iii的点,那么我们只需要判断一下他们之间有没有边可以转移到即可。放一个图可能大家好理解。
只要满足源点到达任意点的距离的权值最小的树就是最短路径生成树,也就是说不唯一。下面代码是非优化版。
#include<iostream>
#include<cstring>
#include<sstream>
#include<cstdio>
#include<algorithm>
#include<queue>
using namespace std;
#define read(x) scanf("%lld",&x)
#define Read(x,y) scanf("%lld%lld",&x,&y)
#define gc(x) scanf(" %c",&x);
#define mmt(x,y) memset(x,y,sizeof x)
#define write(x) printf("%d
",x)
#define INF 0x3f3f3f3f
#define ll long long
#define mod ((1LL<<31) - 1LL)
const ll N = 1005;
const ll M = 1e6;
ll d[N];
bool vis[N];ll id[N];
ll head[N],tot;
ll w[N][N];
struct Edge
{
ll next;
ll to;
ll dis;
}edge[M*2];
inline void add(ll from,ll to,ll dis)
{
edge[++tot].next = head[from];
edge[tot].to = to;
edge[tot].dis = dis;
head[from] = tot;
}
void spfa()
{
mmt(d,0x3f);
mmt(vis,0);
d[1] = 0;
queue<ll> Q;
Q.push(1);
vis[1] = 1;
while(Q.size())
{
ll x= Q.front();
Q.pop();
vis[x] = 0;
for(ll i = head[x];~i;i = edge[i].next)
{
ll y = edge[i].to;
ll dis = edge[i].dis;
if(d[y] > d[x] + dis){
d[y] = d[x ]+dis;
if(!vis[y]){
vis[y] = 1;
Q.push(y);
}
}
}
}
}
bool cmp(ll a,ll b)
{
return d[a] < d[b];
}
void init()
{
mmt(head,-1);
tot = 0;
for(int i = 1;i <=1000;++i){
for(int j = 1;j <= 1000;++j){
w[i][j] = INF;
}
w[i][i] = 0;
}
}
int main()
{
init();
ll n,m;
ll f,t,dis;
Read(n,m);
for(ll i = 1;i <= m;++i){
Read(f,t);read(dis);
if(w[f][t] > dis) w[f][t] = w[t][f] = dis;
add(f,t,dis);
add(t,f,dis);
}
spfa();//先跑一次最短路,求出d数组
for(ll i = 1;i <= n;++i) id[i] = i;
sort(id +1 ,id + n+1,cmp);//按d[ ]从小到大排序
ll ans = 1;
ll cnt = 0;
for(ll i = 2;i <= n;++i){
cnt = 0;
for(ll j = 1;j <= i-1;++j){//模拟最短路径树形成的过程,并按乘法原理统计方案数,
if(d[id[i]] == d[id[j]] + w[id[j]][id[i]]) cnt ++;
}
ans = ans * cnt %mod;
}
cout<<ans<<endl;
}
最短路径生树,边权最小生成树的距离和
也就是说,对于一个边,尽可能的使到达他的边经过松弛,还是上图:
我们这里的话我们应该选了2 3因为这样边权和最小。所以我们接助一个数组来表示到达该点的距离,每次松弛该点时记录最小值,求和即可。
#include<iostream>
#include<cstring>
#include<sstream>
#include<cstdio>
#include<algorithm>
#include<queue>
using namespace std;
#define read(x) scanf("%lld",&x)
#define Read(x,y) scanf("%lld%lld",&x,&y)
#define gc(x) scanf(" %c",&x)
#define mmt(x,y) memset(x,y,sizeof x)
#define write(x) printf("%d
",x)
#define INF 0x3f3f3f3f
#define ll long long
#define mod ((1LL<<31) - 1LL)
const ll N = 3e5+5;
const ll M = 1e6;
ll d[N];
bool vis[N];
ll head[N],tot;
ll p[N];
struct Edge
{
ll next;
ll to;
ll dis;
}edge[N*2];
inline void add(ll from,ll to,ll dis)
{
edge[++tot].next = head[from];
edge[tot].to = to;
edge[tot].dis = dis;
head[from] = tot;
}
struct node
{
ll id,val;
node(){}
node(ll a,ll b):id(a),val(b){}
bool operator <(node A)const{
return val > A.val;
}
};
void dij(ll u)
{
mmt(p,0x7f);
mmt(d,0x7f);
mmt(vis,0);
d[u] = 0;
p[u] = 0;
priority_queue<node> Q;
Q.push({u,0});
node tmp;
while(Q.size()){
tmp = Q.top();
Q.pop();
int x = tmp.id;
if(vis[x]) continue;
vis[x] = 1;
for(int i = head[x];~i;i = edge[i].next){
int y = edge[i].to;
ll dis = edge[i].dis;
if(d[y] >= d[x] + dis){
p[y] = min(p[y],dis);
d[y] = d[x] +dis;
Q.push({y,d[y]});
}
}
}
}
void init()
{
mmt(head,-1);
tot = 0;
}
int main()
{
init();
ll n,m;
ll f,t,dis;
Read(n,m);
for(ll i = 1;i <= m;++i){
Read(f,t);read(dis);
add(f,t,dis);
add(t,f,dis);
}
read(t);
dij(t);
ll ans = 0;
for(int i = 1;i <= n;++i){
ans += p[i];
}
cout<<ans<<endl;
}
网上最短路径生成树大都是矩阵N^2枚举,如果3000点以上那必然会超时。我们换换思想,如果在Djstra出队时只要他更新的权值等于最短路径那么将成为cnt数组之一,也就是说我们不必要N ^2枚举,只要再做一遍Dikjstra就可以了。因为网上没有找到相似的思路,所以程序有很多可以诟病的地方,希望大家指正。
#include<iostream>
#include<cstring>
#include<sstream>
#include<cstdio>
#include<algorithm>
#include<queue>
using namespace std;
#define read(x) scanf("%lld",&x)
#define Read(x,y) scanf("%lld%lld",&x,&y)
#define gc(x) scanf(" %c",&x)
#define mmt(x,y) memset(x,y,sizeof x)
#define write(x) printf("%d
",x)
#define INF 0x3f3f3f3f
#define ll long long
#define mod ((1LL<<31) - 1LL)
const ll N = 1005;
const ll M = 1e6;
ll d[N];
bool vis[N];
ll head[N],tot;
ll p[N];//p[i] 的含义是 源点到 i点的最短路径有几条
struct Edge
{
ll next;
ll to;
ll dis;
}edge[M*2];
inline void add(ll from,ll to,ll dis)
{
edge[++tot].next = head[from];
edge[tot].to = to;
edge[tot].dis = dis;
head[from] = tot;
}
struct node
{
ll id,val;
node(){}
node(ll a,ll b):id(a),val(b){}
bool operator <(node A)const{
return val > A.val;
}
};
void dij(ll u,ll id)
{
mmt(p,0);
if(id == 0) mmt(d,0x7f); // 第2次 保留原来最短路径数组
mmt(vis,0);
d[u] = 0;
p[u] = 1;
priority_queue<node> Q;
Q.push({u,0});
node tmp;
while(Q.size()){
tmp = Q.top();
Q.pop();
int x = tmp.id;
if(vis[x]) continue;
vis[x] = 1;
for(int i = head[x];~i;i = edge[i].next){
int y = edge[i].to;
ll dis = edge[i].dis;
if(d[y] >= d[x] + dis){
if(id == 1) p[y] ++;//第二次开始计数
d[y] = d[x] +dis;
Q.push({y,d[y]});
}
}
}
}
void init()
{
mmt(head,-1);
tot = 0;
}
int main()
{
init();
ll n,m;
ll f,t,dis;
Read(n,m);
for(ll i = 1;i <= m;++i){
Read(f,t);read(dis);
add(f,t,dis);
add(t,f,dis);
}
dij(1,0);//跑 d[] 数组
dij(1,1);//找路径方案数
ll ans = 1;
for(int i =1;i<= n;++i){//累乘
ans = ans*p[i]%mod;
}
cout<<ans;
}