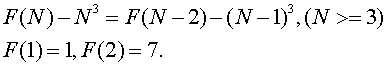
Giving the N, can you tell me the answer of F(N)?
Input
Each test case contains a single integer N(1<=N<=10^9). The input is terminated by a set starting with N = 0. This set should not be processed.
Output
For each test case, output on a line the value of the F(N)%2009.
Sample Input
1
2
3
0
Sample Output
1
7
20
打了个表 4018一循环
#include <bits/stdc++.h>
using namespace std;
int f[6000];
int main()
{
f[1] = 1;
f[2] = 7;
for (int i = 3; i < 4020; i++)
{
f[i] = f[i - 2] + 3 * i * i - 3 * i + 1;
f[i] %= 2009;
}
int n;
while (scanf("%d", &n), n)
{
printf("%d
", f[n % 4018]);
}
}
或者矩阵快速幂分奇数偶数
#include "bits/stdc++.h"
using namespace std;
const int MOD = 2009;
const int MAT[][4] = {
{1, 3, 3, 1},
{0, 1, 4, 4},
{0, 0, 1, 2},
{0, 0, 0, 1}
};
const int TABLE1[] = {1, 4, 2, 1};
const int TABLE2[] = {7, 9, 3, 1};
struct Mat {
int mat[4][4];
Mat() {
memset(mat, 0, sizeof(mat));
}
friend Mat operator * (Mat n, Mat m) {
Mat res;
for (int k = 0; k < 4; k++)
for (int i = 0; i < 4; i++)
for (int j = 0; j < 4; j++)
res.mat[i][j] = (res.mat[i][j] + n.mat[i][k] * m.mat[k][j]) % MOD;
return res;
}
} m;
Mat mat_pow(Mat n, int k) {
Mat res;
for (int i = 0; i < 4; i++) {
res.mat[i][i] = 1;
}
while (k) {
if (k & 1) {
res = res * n;
}
n = n * n;
k >>= 1;
}
return res;
}
int main() {
int n;
while (scanf("%d", &n) && n) {
if (n == 1) {
puts("1");
continue;
}
if (n == 2) {
puts("7");
continue;
}
memmove(m.mat, MAT, sizeof(m.mat));
m = mat_pow(m, n - 1 >> 1);
int res = 0;
if (n & 1) {
for (int i = 0; i < 4; i++) {
res = (res + m.mat[0][i] * TABLE1[i]) % MOD;
}
} else {
for (int i = 0; i < 4; i++) {
res = (res + m.mat[0][i] * TABLE2[i]) % MOD;
}
}
printf("%d
", res);
}
return 0;
}