机器学习--代价函数

一、代价函数概述

机器学习的模型分为能量模型和概率模型，知道概率分布的可以直接用概率模型进行建模，比如贝叶斯分类器，不知道的就用能量模型，比如支持向量机。因为一个系统稳定的过程就是能量逐渐减小的过程。

简单理解，代价函数也就是通常建立的能量方程的一种，在机器学习中用来衡量预测值和真实值之间的误差，越小越好。一般来说一个函数有解析解和数值解，解析解就是我们数学上可以用公式算出来的解，数值解是一种近似解，在解析解不存在或者工程实现比较复杂的时候，用例如梯度下降这些方法，迭代得到一个效果还可以接受的解。所以要求代价函数对参数可微。

代价函数、损失函数、目标函数并不一样，这一点后边再介绍，这篇文章就先只介绍代价函数。

• 损失函数： 计算的是一个样本的误差

• 代价函数： 是整个训练集上所有样本误差的平均

• 目标函数： 代价函数 + 正则化项

在实际中，损失函数和代价函数是同一个东西，目标函数是一个与他们相关但更广的概念。

• 代价函数（Cost Function）： 在机器学习中，代价函数作用于整个训练集，是整个样本集的平均误差，对所有损失函数值的平均。

二、代价函数的作用：

1.为了得到训练逻辑回归模型的参数，需要一个代价函数，通过训练代价函数来得到参数。
2.用于找到最优解的目标函数。

三、代价函数的原理

在回归问题中，通过代价函数来求解最优解，常用的是平方误差代价函数。有如下假设函数：
$h(x)=A+Bx$

假设函数中有A和B两个参数，当参数发生变化时，假设函数状态也会随着变化。 如下图所示

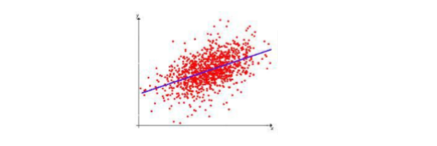
想要拟合图中的离散点，我们需要尽可能找到最优的AAA和BBB来使这条直线更能代表所有数据。如何找到最优解呢，这就需要使用代价函数来求解，以平方误差代价函数为例，假设函数为$h(x)= heta_0x$

平方误差代价函数的主要思想就是将实际数据给出的值与拟合出的线的对应值做差，求出拟合出的直线与实际的差距。在实际应用中，为了避免因个别极端数据产生的影响，采用类似方差再取二分之一的方式来减小个别数据的影响。因此，引出代价函数：

$J( heta _0, heta _1)=frac{1}{2m}sum_{i=1}^{m}(h(x^{(i)})-y^{(i)})^2$
最优解即为代价函数的最小值 $minJ( heta _0, heta _1)$
如果是 1 个参数，代价函数一般通过二维曲线便可直观看出。如果是 2 个参数，代价函数通过三维图像可看出效果，参数越多，越复杂。

四、代价函数非负：

目标函数存在一个下界，在优化过程当中，如果优化算法能够使目标函数不断减小，根据单调有界准则，这个优化算法就能证明是收敛有效的。
只要设计的目标函数有下界，基本上都可以，代价函数非负更为方便。

五、代价函数分类

1. 均方差代价函数
   
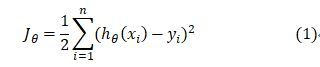
   这个是来自吴恩达的机器学习课程里面看到的损失函数，在线性回归模型里面提出来的。表示模型所预测（假设）的输出，是真实的输出，即label。
   个人猜测，均方差应该是
   
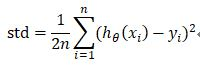
   由于对给定的数据集来说，n是确定的值，因此，可以等同于式(1)。

这个形式的代价函数计算Jacobian矩阵如下：

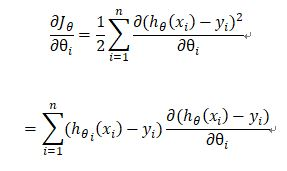
2. 对数损失函数
   对数似然作为代价函数是在RNN中看到的，公式如下：
   
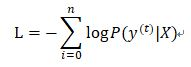
   表示真实目标在数据集中的条件概率的负对数。其意义在于，在很多预测目标概率的模型中，将最大概率对应的类型作为输出类型，因此，真实目标的预测概率越高，分类越准确，学习的目标是真实目标的预测概率最大化。而概率是小于1的，其对数值小于0，且对数是单调递增的，因此，当负对数最小化，就等同于对数最大化，概率最大化。
   逻辑回归中的代价函数实际上就是对数似然的特殊表示的方式：
   
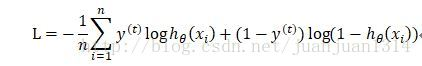
   二项逻辑回归的输入$h_{ heta}(x_i)$是预测目标为1的概率，$y^{(t)}$的值为1或0.因此，$1-h_{ heta}(x_i)$目标为0的概率为，当真实的目标是1时，等式右边第二项为0，当真是目标为0时，等式右边第一项为0，因此，对于单个样本，L就是负对数似然。
   同理，对于softmax回归的概率函数为
   
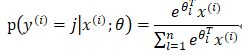
   未添加权重惩罚项的代价函数为
   

3.交叉熵
交叉熵在神经网络中基本都用交叉熵作为代价函数。

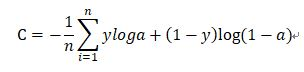
这和逻辑回归的代价函数很像，y作为真实的目标（label），不一定是二值的，且a不是预测目标的概率，而是神经网络的输出，
它的原理还不是很明白，据说在神经网络中用交叉熵而不用均方差代价函数的原因是早期的神经元的激活函数是sigmoid函数，而此函数在大部分取值范围的导数都很小，这样使得参数的迭代很慢。
而交叉熵的产生过程网友是这样推导的：

博客参考 吴恩达的机器学习公开课！