1.关于BFS的Key_word:
①hash或状态压缩记录状态 ②状态剪枝 ③反向BFS ④双向BFS ⑤特殊初始化VIS数组 ⑥动态图的搜索 ⑦优先队列优化搜索 ⑧数位搜索
下面是一一讲解:
1.hash或状态压缩记录状态 :
当状态太多而且边界也广时数组难以存储状态时或者题目对空间的要求较为苛刻,这时候就要使用状态压缩来保存所需的状态或者hash的方式将一个状态对应为一个整数通过一维数组来记录是否访问,当数据过于离散时可以考虑使用map,但是相应的时间复杂度也会上升,如果真的要将所有状态限定在一个较小的范围,可以使用双hash,不过一般的状态相对来说不会太难表示,而是考察对于每个搜索状态的如何设计转移,有点像DP,谁让DP搜索不分家。
2.状态剪枝:
没有剪枝的搜索是没有灵魂的,无论DFS还是BFS,对于DFS而言我们是一层一层的寻找,当我们知道某一子树不可能找的结果,或者说这一状态在具有更有条件时访问过便不再扩展,但是并不代表着,我小于当前最优解就意味着我的子树中不存在最优解,这一段的说明见⑦。但是剪枝需要严谨的证明过程,盲目的剪枝不可取,要根据题目具体设计在状态转移中的剪枝条件,这个在BFS中没有什么规律可循,每一道题都意味着你需要在题目中发掘隐含条件进行剪枝,例如:当到达同一状态时,Dis1<Dis2,那么显而易见,Dis2的后续就要被剪掉,因为在这一点具有同样的转移的后续,但是在这一点有最优的选择,且最优选择的结果一定好于所有其他选择,那么进行剪枝,那么会发现只有着明确的相似关系,且有着明显的先后优劣状态的状态需要剪枝,但是在题目中很难找到一眼可以剪枝的关系,这就需要进一步的推导与证明,当这一点学好之后,对于DP的学习会发现,经过各种剪枝的搜索就是DP,不采取递归手段访问每一可能的状态。
3.反向BFS:
例如,在一个迷宫中有N个人,请找出最快走出迷宫的那个人? 那么我们正向考虑问题,对于N个人那么他们快走出迷宫的话需要求N次BFS,比较步数,那么当N大到一定程度时,爆栈,不需要很大图就会爆栈,那么反向考虑,我们换种问法,迷宫中有一个人,有N个出口,请问他最快从哪个出口中走出? 如果这么问,我们一定会思路泉涌,但是题目绝对不会出这么简单地变换,我们在改造一下这个问题,有N个人M个出口的题目我们该如何解决,一种解决方法是建图,Floyd求最短路比较大小时间复杂度为O((N+M)^3+(N+M)^2), 我们这里给出BFS的方式,至于时间复杂度只能说随缘,但是思路何尝不是一个好思路,我们先比较N和M的大小,通过小的作为搜索起点,那么我们第一次搜索的Dis设置为最优解,第二次搜索时若大于Dis还无解,一定无解,跳出,通过不断搜索的不断更新最优解的方式搜索复杂度应该在 O(MIN(N,M)*ans)——O(MIN(N,M)*dis first)之间,那么遍历图上的任何点的时间为(N+M)^2,在乘以min(N,M),那么时间复杂度最大是个(N+M)^2*Min(n,m),对于时间复杂度一定优于第一种,对于其他的方法可以使使用队列优化的dijkstra,O((N+M)*Log(N+M)*min(N,M))的复杂度,对于更好的方法现在,我还不太清楚,当然最短路不在我们的讨论范围内,因为有些情况是不能处理的,访问与后续,所以稍稍改动就只能使用BFS。
4.双向BFS
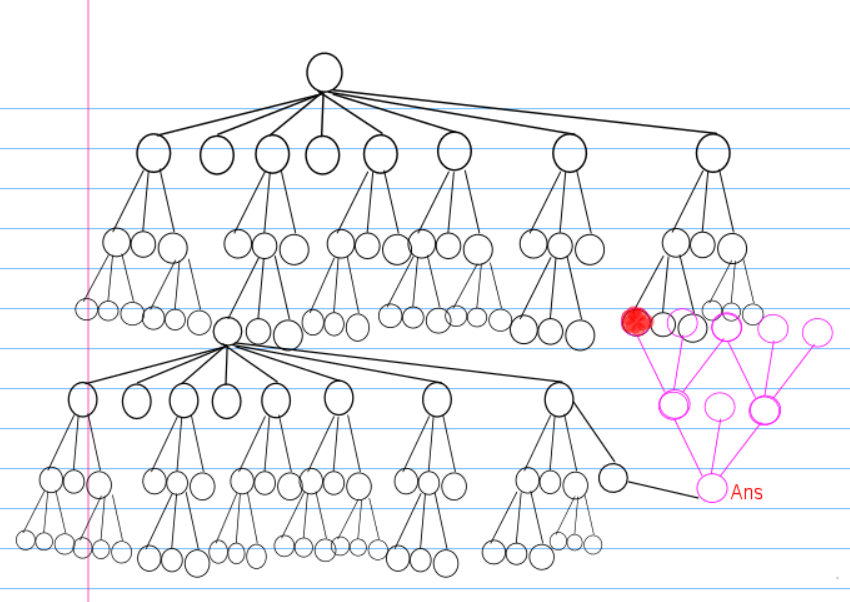
无论从ans还是从start开始扩展,都以几何的趋势增长无论从哪一方开始搜索都会爆栈,但是ans与start之间的路很少,通过双向搜索找到中间点这种方式绝对会更加快速,图比较丑也不太形象,但大体的思想还是表现出来。适用于状态转移方向太多,但是距离较短的的情况。
5.特殊化的VIS数组
对于一张图我们vis=1时为访问,vis=0时为未访问,第二次用的时候就需要memset,但是时间太长,我们换一种思想,对于vis=n时,为访问过,vis!=1为未访问,那么如果vis中的没有N的话那就不用初始化了,那么对于第一遍之后的vis数组之后1或0,那么我们使n=2,即可不用初始化,第三遍时等于3,以此类推。
6.动态图的搜索
图的情况会随时间轴改变,那么需要在状态的维度中增加一个时间维度,而且不同时间的状态不同,同状态不同时间理解为不同的状态,那么对于动态图的搜索,不能简单vis数组,而是要记录时间轴,状态的叠加。
7.优先队列搜索
对于优先队列优化的搜索,必须要证明当前的最优解的扩展一定比不是最优解的扩展要优,即当前不是最优未来一定不是最优。不然使用优先队列优化的搜索必错。
8.数位搜索
这个搜索虽然写到这,不是需要注意什么,而是说数位搜索很基础,不太好像,但是一定能做。更多的是K进制数,用除法求余什么。比如一个500位的数,怎么取模?
想想小学的除法算式怎么写? 不是一位一位的除吗?多少位的也可以做。