【树3】满二叉树、完全二叉树、完美二叉树

---------注：本文所用的术语定义均来自国外大学和计算机文献使用的定义，非国内教材。层次编号从1开始-------------

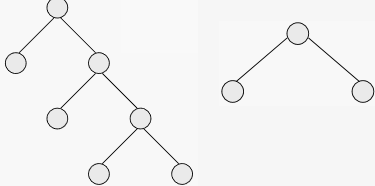
满二叉树（Full Binary Tree）

定义：a binary tree T is full if each node is either a leaf or possesses exactly two child nodes.

大意：每一个结点要么度为0（是叶子结点），要么度为2（有2个孩子结点）。

图例：

性质：如果T是一个非空满二叉树，则

(a) 如果有 N₂ 个 非叶子结点，则 叶子结点的个数 是 N₂+1

(b) 如果有 N₂ 个 非叶子结点，则总的结点数是 2N₂+1

(c) 如果总结点数是N ，则非叶子结点个数是 (N-1)/2

(d)  如果总结点数是N， 则叶子结点个数是 (N+1)/2

(e) 如果有N₀ 个叶子结点，则总结点数是2N₀-1

(f) 如果有N₀ 个叶子结点，则非叶子结点数是N₀-1

也就是说，在一个非空满二叉树中，只要你知道了 【总结点数 N ，叶子结点数N₀ ， 非叶子结点数 N₂ 】 三者之一，就可以推导出其它二者的值。

证明：

(a) 设度为2的结点（非叶子结点）个数为N₂，度为0的结点（叶子结点）个数为N₀，总结点数为N。边有E条。

N₂+N₀ = N

N - 1 = L (树的边数比结点数少1)

2N₂ = L  ( 边都是度为2的结点引出的，且引出2条 )

联立得：N₀ = N₂+1

证明： 

(b) 

N₂+N₀ = N

N₀ = N₂+1  (   由(a)  可知  )

联立得：N =2N₂+1

......

其余的都可以由（a）中的结论轻松推导出，不再赘述。

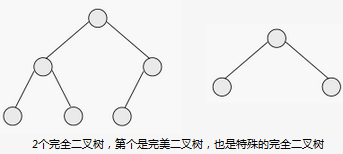
完全二叉树（Complete Binary Tree）

定义：a binary tree T with n  levels is complete if all levels except possibly the last are completely full,and the last level has all its nodes to the left side.

大意：除了最后一层可能不是”满的“，其它层都必须是”满的“，且最后一层的结点都在左边连续出现。

注意：

1、”满的“意思是，这一层的节点数达到最大值。

2、最后一层可能不是”满的“，说明可以存在是”满的“情况，如果是这样，那就是一个完美二叉树。完美二叉树是特殊的完全二叉树。

通俗的说，完全二叉树从root到 倒数第二层 之间形成是完美二叉树，而最后一层可以不是”满的“，也可以是”满的“，如果不是”满的“，则最后一层的结点必须靠左连续出现。

图例：

性质：

1、总结点数是n，则有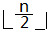个非叶子结点（内部结点）

⌊ n / 2 ⌋ {displaystyle lfloor n/2 floor } 个内部结点。

2、总结点数是n，则层次数是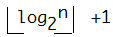

3、完全二叉树可以使用数组来作为高效的存储实现，因为完全二叉树的逻辑关系可以通过结点的编号运算得来，且这种关系对于所有的完全二叉树都是固定的。如果使用链式的，则需要浪费空间，访问速度也不如数组。 下面给出运算规律：

给完全二叉树的结点，从上到下，从左到右依次从0开始编号作为这个结点的索引，则：

 

如果i==0，则它是root结点。

如果i >0 ，则他的父结点的索引为:

 

如果 2*(i+1) > n ，则它无左孩子，那么他一定是叶子结点。

       2*(i+1) <=n ,  则他的左孩子的索引为  2i +1

 

如果 2*(i+1)+1 >  n，则他无右孩子。

        2*(i+1)+1 <=  n，则它的右孩子的索引为 2i+2

 

完美二叉树

定义：A binary tree with all leaf nodes at the same depth. All internal nodes have degree 2.

大意：所有的非叶子结点的度都达到最大值2，叶子结点都在同一层，也就是最下层。

图例：

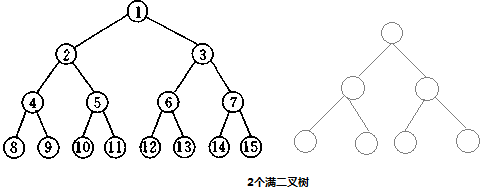
任何一个完美二叉树 既属于满二叉树，也属于完全二叉树。因此它拥有满二叉树和完全二叉树的所有性质

完美二叉树从外观上看他是一个等边三角形。他的每一层都被填充满。

性质

1、层数为k的完美二叉树，其总结点数为 2^k  - 1    (k>=1)

2、第i层结点数是 2^(i-1)         (i>=1)

3、因为完美二叉树既属于完全二叉树，因此可以使用数组来作为高效的存储实现。