题目:
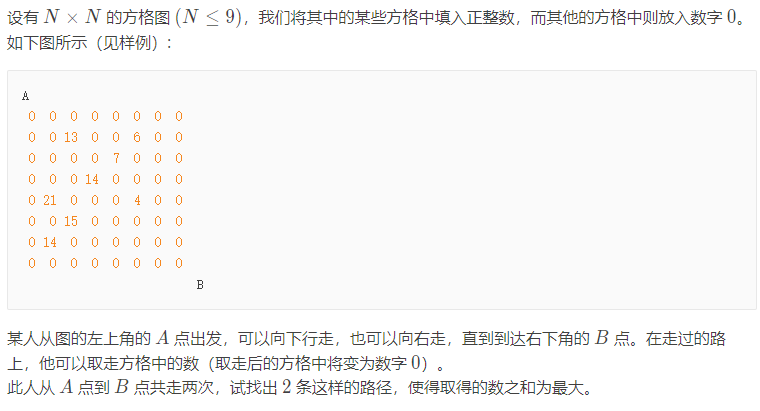
思路:
我拿过这题一看,方格,下&右
好又是这种,和过河卒差不多
不过这题有点特殊:
1.能走两遍,前一次的路对后一次有影响
2.与过河卒相比,它不是计数,而是求最大值
但是本质上都是一样的
对于第一点,我们可以用多线程的方式解决,也就是同时处理两条路径
对于第二点,无非就是将加法换成了求max
转移方程应运而生:
f[i][j][k][l]=max(f[i-1][j][k-1][l],f[i-1][j][k][l-1],f[i][j-1][k-1][l],f[i][j-1][k][l-1])+mp[i][j]+mp[k][l];
要特判一下i==k&&j==l的情况
代码:
#include <bits/stdc++.h> using namespace std; int n; int mp[15][15]; int DP[15][15][15][15]; int main() { scanf("%d",&n); while(1) { int tx,ty,tz; scanf("%d %d %d",&tx,&ty,&tz); if(!tx&&!ty&&!tz) break; mp[tx][ty]=tz; } for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) for(int k=1;k<=n;k++) { int l=i+j-k; if(l<=0) break; DP[i][j][k][l]=max(DP[i-1][j][k][l-1],max(DP[i-1][j][k-1][l],max(DP[i][j-1][k][l-1],DP[i][j-1][k-1][l]))); if(i==k&&j==l) DP[i][j][k][l]+=mp[i][j]; else DP[i][j][k][l]+=mp[i][j]+mp[k][l]; } printf("%d ",DP[n][n][n][n]); return 0; }