凸包——Graham扫描法和Andrew算法

凸包：能围住所有给出的点的面积最小的多边形（个人理解）

Graham：选取y值最小的点，将其它点极角排序，依次把1~n号点加入栈中，判断当前点、栈顶、栈顶下面那个点三者的关系（嘻嘻），一直这样做就好了

判断用叉积，也就是如下图的要判掉（top--）

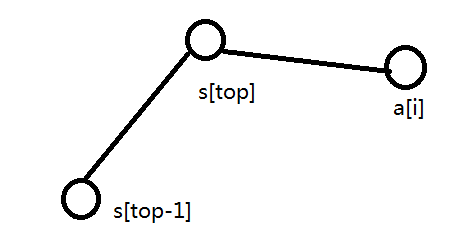
其实上图是不对的哦，你有没有反应过来呢~按极角排序后不会有这种情况哦，肯定是先连a[i]，再连s[top]的

具体实现看代码吧~

#include<cstdio>
#include<cmath>
#include<algorithm>
#define sqr(x) (x)*(x)
#define rep(i,x,y) for (int i=(x);i<=(y);i++)
#define per(i,x,y) for (int i=(x);i>=(y);i--)
typedef double DBD;
using namespace std;
const int N=100010;
struct point{int x,y;}a[N],s[N],b[N];
int n,top;
int read() {int d=0,f=1; char c=getchar(); while (c<'0'||c>'9') {if (c=='-') f=-1; c=getchar();} while (c>='0'&&c<='9') d=(d<<3)+(d<<1)+c-48,c=getchar(); return d*f;}
DBD dis(int x,int xx,int y,int yy){return sqrt(sqr(x-xx)+sqr(y-yy));}
bool cross(point x,point y,point z){return (x.x-z.x)*(y.y-z.y)-(y.x-z.x)*(x.y-z.y)>=0;}
bool cmp(point A,point B){return (A.x-a[1].x)*(B.y-a[1].y)-(B.x-a[1].x)*(A.y-a[1].y)>=0;}
int main()
{
    //judge();
    n=read();
    int p=0; a[0].y=1e9;
    rep(i,1,n)
    {
        a[i].x=read(); a[i].y=read();
        if (a[i].y<a[p].y||a[i].y==a[p].y&&a[i].x<a[p].x) p=i;
    }
    swap(a[1],a[p]);
    sort(a+2,a+1+n,cmp);
    s[1]=a[1]; s[2]=a[2]; top=2;
    rep(i,3,n)
    {
        while (top>=2&&cross(a[i],s[top],s[top-1])) top--;
        s[++top]=a[i];
    }
    DBD ans=0;
    for (int i=1;i<top;i++) ans+=dis(s[i].x,s[i+1].x,s[i].y,s[i+1].y);
    ans+=dis(s[1].x,s[top].x,s[1].y,s[top].y);
    printf("%.1lf",ans);
    return 0;
}

Andrew：

据说比Graham更快更稳定，但我不是很懂。。。

具体过程（哪里具体了。。。）：将所有点以x为第一关键字，y为第二关键字排序，分别求出上下凸壳，求的时候一样的判法，就好了

#include<cstdio>
#include<cmath>
#include<algorithm>
#define sqr(x) (x)*(x)
#define rep(i,x,y) for (int i=(x);i<=(y);i++)
#define per(i,x,y) for (int i=(x);i>=(y);i--)
typedef double DBD;
using namespace std;
const int N=100010;
struct point{int x,y;}a[N],s[N];
int n,top;
int read() {int d=0,f=1; char c=getchar(); while (c<'0'||c>'9') {if (c=='-') f=-1; c=getchar();} while (c>='0'&&c<='9') d=(d<<3)+(d<<1)+c-48,c=getchar(); return d*f;}
DBD dis(int x,int xx,int y,int yy){return sqrt(sqr(x-xx)+sqr(y-yy));}
DBD cross(point x,point y,point z){return (x.x-z.x)*(y.y-z.y)-(y.x-z.x)*(x.y-z.y);}
bool cmp(point a,point b){return a.x<b.x||a.x==b.x&&a.y<b.y;}
int main()
{
    n=read();
    rep(i,1,n) a[i].x=read(),a[i].y=read();
    sort(a+1,a+1+n,cmp);
    rep(i,1,n)
    {
        while (top>1&&cross(a[i],s[top],s[top-1])>=0) top--;
        s[++top]=a[i];
    }
    int k=top;
    per(i,n-1,1)
    {
        while (top>k&&cross(a[i],s[top],s[top-1])>=0) top--;
        s[++top]=a[i];
    }
    DBD ans=0;
    rep(i,1,top-1) ans+=dis(s[i].x,s[i+1].x,s[i].y,s[i+1].y);
    ans+=dis(s[1].x,s[top].x,s[1].y,s[top].y);
    printf("%.1lf",ans);
    return 0;
}

可能你会疑问：为什么第n个点一定在凸包上呢？当然了，因为它的x最大，即使有和它x一样的，它的y更大，yy一下就脑补出来了