一.学习
1. 定义:如果一个计算机程序针对某类任务T的用户P衡量的性能根据经验E来自我完善。那么我们称这个计算机程序在经验E中学习,针对某类任务T,它的性能用P来衡量。
例如:西洋跳棋学习问题
任务T:下西洋跳棋
性能标准P:比赛中击败对手的百分比
训练经验E:和自己进行对弈
2.设计一个学习系统
1.选择训练经验
训练经验的属性:
训练经验能否为系统的决策提供直接或间接的反馈
学习器可以在多大程度上控制训练样例序列
训练样例的分布能多好地表示实例分布,通过样例来衡量最终系统的性能P
2.选择目标函数
目标函数V,V:B->A来表示V把任何合法的棋局从集合B映射到某一个实数值。我们让这个目标函数V给好的棋局赋予较高的评分。如果系统能够成功地学习这个目标函数V,那么它便能使用此函数轻松地找到当前棋局的最佳走法。实现方法是,先产生每一个合法走了的所有后续棋局,然后使用V来选取其中最佳的后续棋局,从而选择最佳走子。
对于集合B中的任意的棋局状态b,我们如许定义目标函数V(b):
1)如果b是一最终的胜局,那么V(b)=100
2)如果b是一最终的负局,那么V(b)=-100
3)如果b是一最终的和局,那么V(b)=0
4)如果b不是最终棋局,那么V(b)=V(b'),其中b'是从b开始双方都采取最优对弈后可到达的终局。
3.选择目标函数的表示
对于任何给定的棋盘状态,函数V可以通过以下棋盘参数的线性组合来计算:
x1:棋盘上黑子的数量
x2:棋盘上红子的数量
x3:棋盘上黑王的数量
x4:棋盘上红王的数量
x5:被红子威胁的黑子数量(即会在下一次被红子吃掉的黑子数量)
x6:被黑子威胁的红子数量
V(b)=w0+w1x1+w2x2+w3x3+w4x4+w5x5+w6x6
西洋跳棋程序的部分设计:
任务T:下西洋跳棋
性能标准P:世界锦标赛击败对手的百分比
训练经验E:和自己对弈
目标函数:V:Board->A
目标函数的表示:V(b)=w0+w1x1+w2x2+w3x3+w4x4+w5x5+w6x6
4.选择函数逼近算法
把任何中间棋局b的训练值Vtrain(b)赋予V^(Successor(b)),其中V^是学习器目前采用的V的近似函数,Successor(b)表示b之后再轮到程序走棋时的棋盘状态(也就是程序走了一步和对手回应一步后的棋局)。估计训练值的方法可被归纳为:
训练值估计法则:
Vtrain(b)<-V^(Successor(b))
最佳假设:E Ξ ∑<b,Vtrain(b)>¢ traninning examples(Vtrain(b)-V^(b))2
5.最终设计
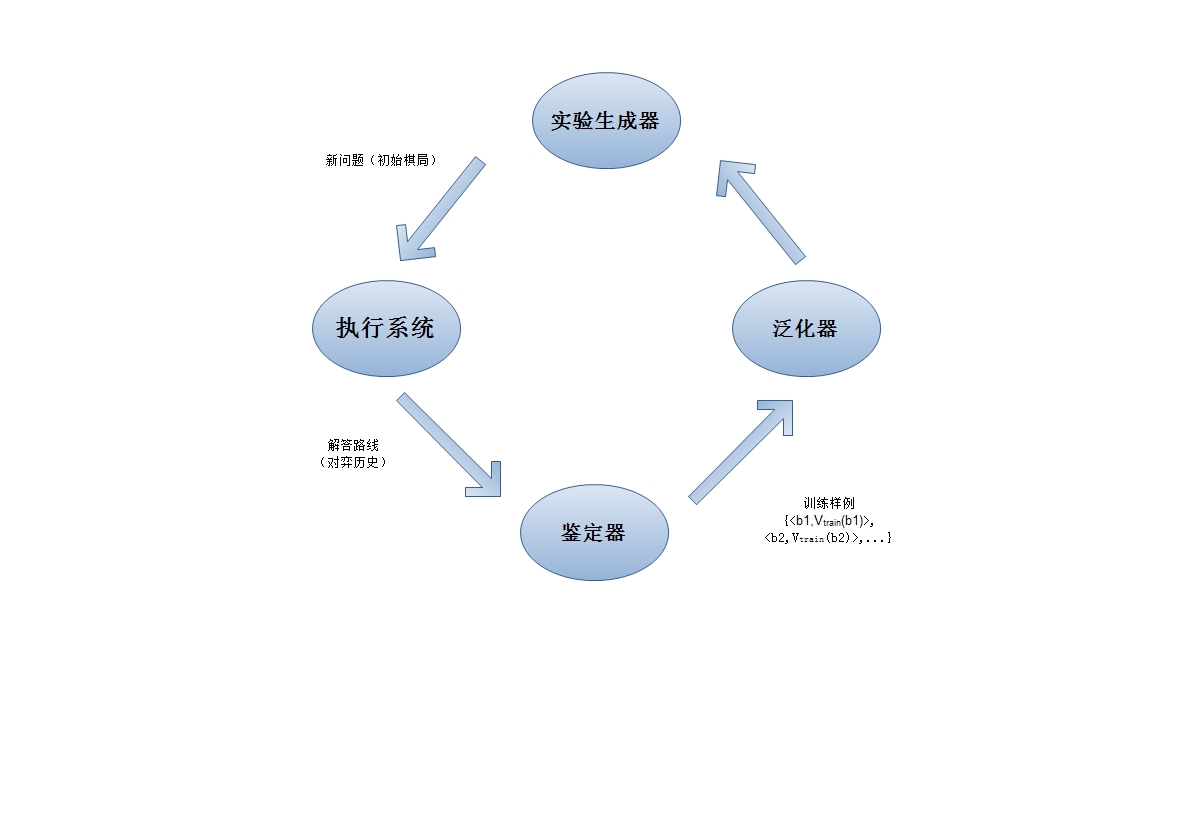
西洋跳棋学习程序的最终设计
执行系统(Performance System):用学会的目标函数来解决给定的任务,在此就是对弈西洋跳棋。它把新问题(新一盘棋)的实例作为输入,产生一组解答路线(对弈历史记录)作为输出。
鉴定器(Critic):它以对弈的路线或历史记录作为输入,输出目标函数的一系列训练样例。
泛化器(Generalizer)它以训练样例作为输入,产生一个输出假设,作为它对目标函数的估计。
实验生成器(Experiment Generator)它以当前的假设(当前学到的函数)作为输入,输出一个新的问题供执行系统去探索。