时间复杂度


小结:

空间复杂度

算法可视化网站推荐
冒泡排序
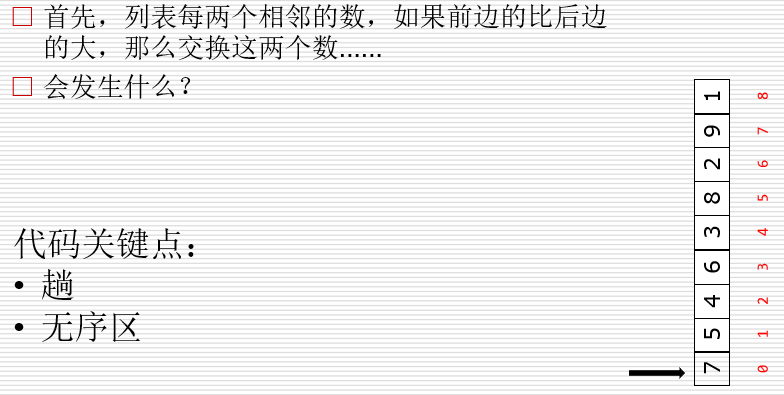

### 冒泡排序 (************) ### 时间复杂度:最差的情况:O(n^2) 最好的情况:O(n) 空间复杂度:O(1) 并没有开辟新的储存空间 def bubble_sort(li): for i in range(len(li)-1): flag = True #用于优化 for j in range(len(li)-1-i): if li[j] > li[j+1]: li[j], li[j+1] = li[j+1], li[j] flag = False if flag: return li = [7,5,4,6,3,8,2,9,1] bubble_sort(li) print(li)
选择排序

### 选择排序 ### 时间复杂度是:O(n^2) def select_sort(li): for i in range(len(li)): minLoc = i for j in range(i+1, len(li)): if li[minLoc] > li[j]: li[minLoc], li[j] = li[j], li[minLoc]
插入算法
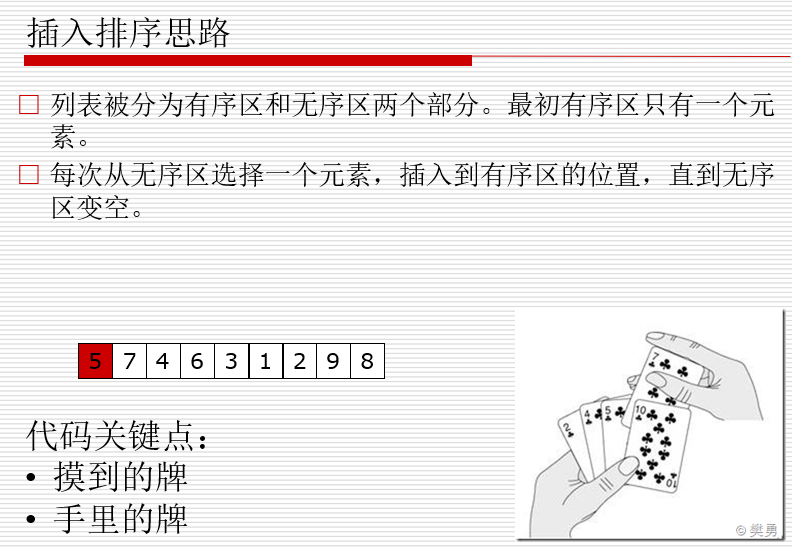
### 插入排序 ### 时间复杂度是:O(n^2) def insert_sort(li): for i in range(1, len(li)): ### i=2 tmp = li[i] ## tmp=li[2]=4 j = i - 1 ### j = 1 li[1]=7 while j >= 0 and li[j] > tmp: li[j+1] = li[j] ### [5,7,7,6,3,8,2,9,1] ==> [5,5,7,6,3,8,2,9,1] j = j - 1 ### j = 0 j= -1 li[j+1] = tmp
优化空间: 应用二分查找来寻找插入点
小结:

快速排序

# 快排 ##### 时间复杂度是:O(nlogn) def partition(li, left, right): #### O(n) tmp = li[left] while left < right: while left < right and li[right] >= tmp: right = right - 1 li[left] = li[right] while left < right and li[left] <= tmp: left = left + 1 li[right] = li[left] li[left] = tmp return left def quick_sort(li, left, right): if left < right: mid = partition(li, left, right) ### 归位函数 quick_sort(li, left, mid-1) #### O(logn) quick_sort(li, mid+1, right) li = [7,5,4,6,3,8,2,9,1] quick_sort(li,0,len(li)-1) print(li)
上述4中方法时间比较
import time,random start = time.time() li = [random.randint(0,100000) for i in range(10000)] bubble_sort(li) print('bubble_sort:',time.time()-start) # 8.805101871490479 start = time.time() li = [random.randint(0,100000) for i in range(10000)] select_sort(li) print('select_sort',time.time()-start) # 4.129027366638184 start = time.time() li = [random.randint(0,100000) for i in range(10000)] insert_sort(li) print('insert_sort',time.time()-start) # 3.236048460006714 start = time.time() li = [random.randint(0,100000) for i in range(10000)] quick_sort(li,0,len(li)-1) print('quick_sort',time.time()-start) # 0.029005050659179688
希尔算法(了解)

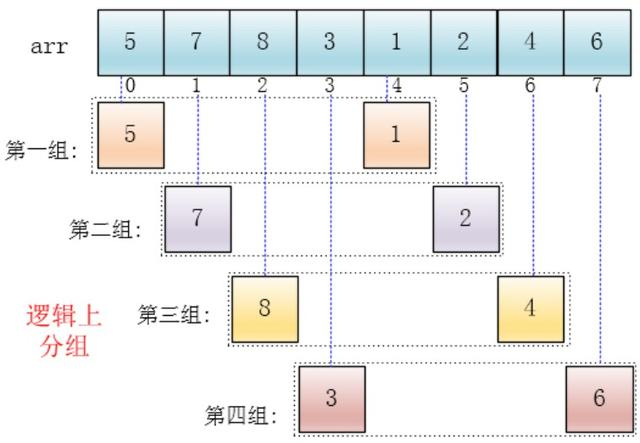
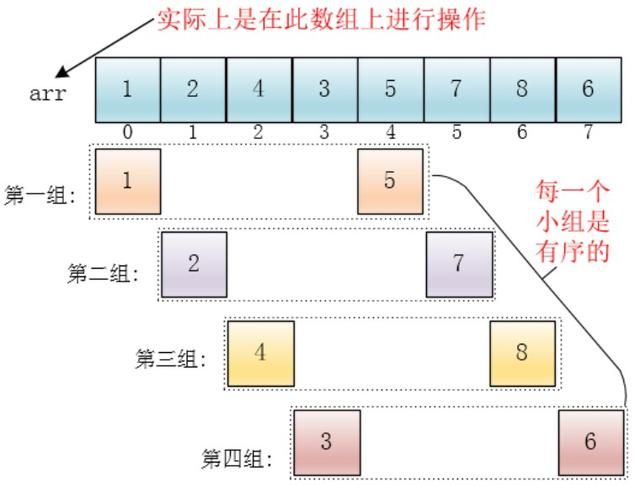
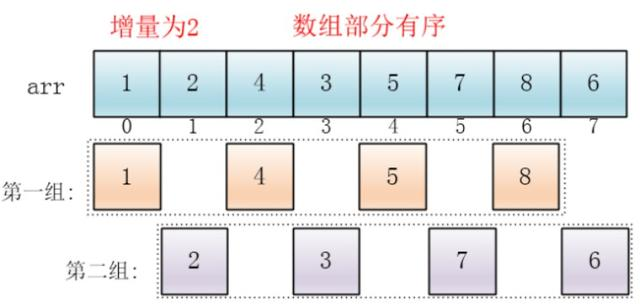
代码:


小结:


计数排序(了解)
# 假如有一列数组为 # [7,5,4,6,3,8,2,9,1,9] 对他进行计数 # [0,1,1,1,1,1,1,1,1,2] 代表0有0个,1有1个,2有1个...9有2个
# 计数排序 def count_sort(li): # 因为时间复杂度没有系数,所以整体复杂度算O(n) count = [0 for _ in range(10)] print(count) # [0, 0, 0, 0, 0, 0, 0, 0, 0, 0] for k in li: # 此循环时间复杂度O(m) count[k] += 1 print(count) # [0, 1, 1, 1, 1, 1, 1, 1, 1, 2] li.clear() # 下面循环时间复杂度O(n) for k,v in enumerate(count): for i in range(v): # 这层时间复杂度可以忽略不计 li.append(k) li = [5,7,4,6,3,8,2,9,1,9] count_sort(li) print(li) # [1, 2, 3, 4, 5, 6, 7, 8, 9, 9]
算法拓展:
动态规划 贪心(分糖果,人民币问题) 背包问题
二分法查找


##### 二分查找 时间复杂度O(logn) def bin_search(li, value , low, high): if low<=high: mid = (low+high) // 2 if li[mid] == value: return mid elif li[mid] > value: return bin_search(li, value, low, mid-1) else: return bin_search(li, value, mid+1, high) else: return li = [1,2,3,4,5,6,7,8,9] index = bin_search(li, 3, 0, len(li)-1) print(index)