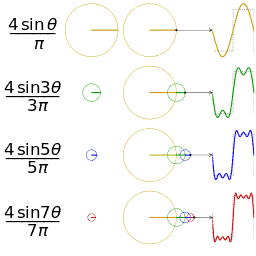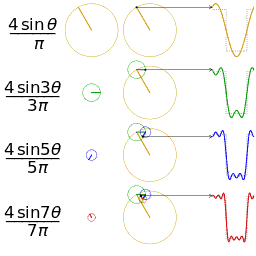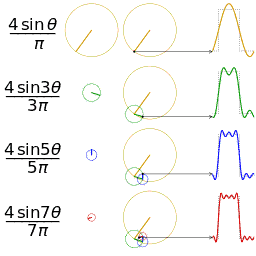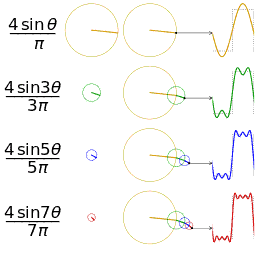1、傅里叶同学告诉我们,任何周期函数,都可以看作是不同振幅,不同相位正弦波的叠加
2、在你的理解中,一段音乐是什么呢?
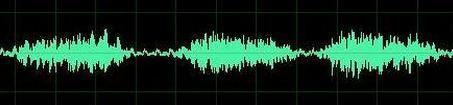 (时域)
(时域)
上图是我们对音乐最普遍的理解,一个随着时间变化的震动。但我相信对于乐器小能手们来说,音乐更直观的理解是这样的:
 (频域)
(频域)
其实这一段写到这里已经可以结束了。上图是音乐在时域的样子,而下图则是音乐在频域的样子。所以频域这一概念对大家都从不陌生。
个人的理解是这样的,乐谱上标注的是单一时刻的各种音乐的叠加类型和变音类型,实际实际演奏中会把声音叠加在一起,成了一个特殊的声音。
对于频率来说,其实也是各种频率叠加起来的,最终合成一个特殊的频率。那为什么不直接定义这个频率呢?对于实际生活中,频率太多了,没办法
一一定义只好在频域定义,特别是噪音可能有10种声音和在一起出来的,就像单词,我们只有26个字符,但是可以表达很多的意思,字母就是26个单
一的频,发声就是时域,组成就是频域。
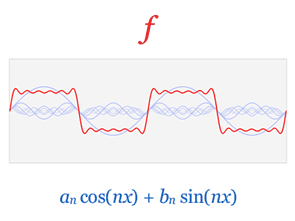
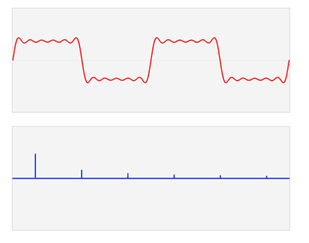
3、傅里叶变换将函数的时域(红色)与频域(蓝色)相关联。频谱中的不同成分频率在频域中以峰值形式表示,这边有一个挺好的图例说明

红色时域 蓝色频域
我能用前面说的正弦曲线波叠加出一个带90度角的矩形波来,你会相信吗?还是先举个栗子并且有图有真相再回答。
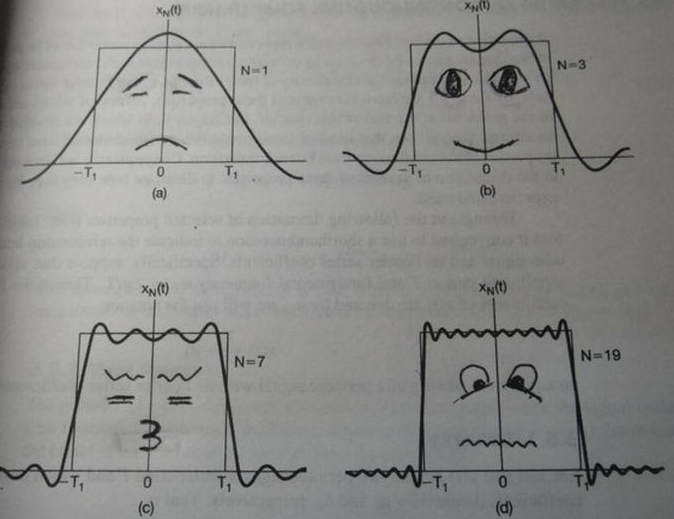
第一幅图是一个郁闷的正弦波cos(x);第二幅图是2个卖萌的正弦波的叠加cos(x)+a.cos(3x);第三幅图是4个发春的正弦波的叠加;
第四幅图是10个便秘的正弦波的叠加;但是要多少个正弦波叠加起来才能形成一个标准90度角的矩形波呢?不幸的告诉大家,答案是无穷多个。
现在再来看那个动图,至少前面两张看得懂了把。
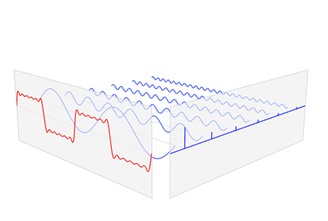
那么第三张图怎么理解呢?其实只要我的时域波形按照频域这样子给就可以的到你想要的的波形,其实就是这个时域波形的形成公式;再来一张图帮助下理解
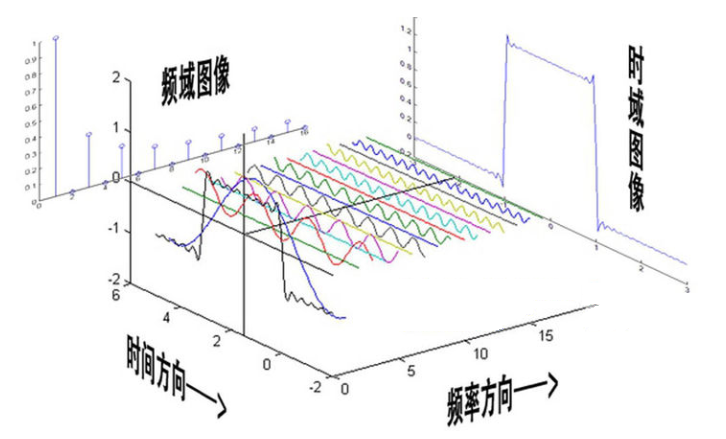
可以发现,在频谱中,偶数项的振幅都是0,也就对应了图中的彩色直线。振幅为0的正弦波。这个要注意。
娱乐看图时间