01背包问题

一个可以装v容量的包，有n个物品可以放到包里面，不能超过容量v。每个物品有对应的重量和价值，保存在数组weight[n]和value[n]中。n个物品对应的只有一个，即要么放第i个物品，第i个物品要么不放。求最大价值

这是个01背包问题，可以用动态规划。测试数据如下

    // int[] weight = {5, 4, 6, 3}
    // int[] value = {10, 40, 30, 50}
    // n = 4 v = 10

weight存物品重量，value存物品价值， n表示物品个数，v表示背包容量

递推公式res[i][j] = max{res[i-1][j], res[i - 1][j - weight[i]] + value[i] }

rest[i][j] 表示前i个物品放到容量为j的最大价值。第i个物品，不放到容量j的包中的价值为res[i-1][j],  放的价值res[i - 1][j - weight[i]] + value[i]。取这两种场景的最大值

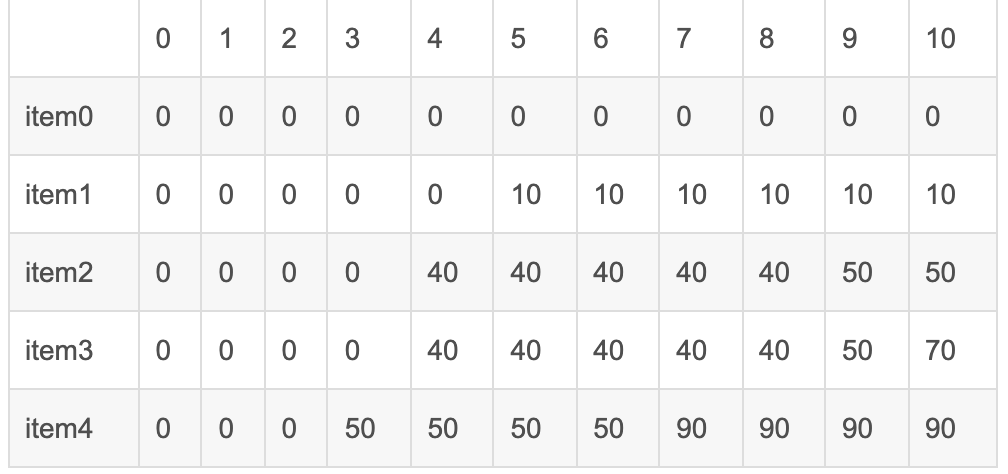
java代码

public class PackageDemo {

    public static void main(String[] args) {
        int[] weight = {5, 4, 6, 3};
        int[] value = {10, 40, 30, 50};
        int n = 4;
        int v = 10;
        System.out.println(new PackageDemo().maxZeroOnePackage(weight, value, n, v));
    }

    // int[] weight = {5, 4, 6, 3}
    // int[] value = {10, 40, 30, 50}
    // n = 4 v = 10
    public int maxZeroOnePackage(int[] weight, int[] value, int n, int v) {
        int[][] res = new int[n + 1][v + 1];
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= v ; j++) {
                // res[i][j] = max{res[i - 1][j], res[i - 1][j - weight[i]] + value[i]}
                if (j < weight[i - 1])
                    res[i][j] = res[i - 1][j];
                else
                    res[i][j] = Math.max(res[i - 1][j], res[i - 1][j - weight[i - 1]] + value[i - 1]);
            }
        }
        return res[n][v];
    }
}

结果为90