以逻辑回归模型为基础!之前先把逻辑回归的知识看看
1.
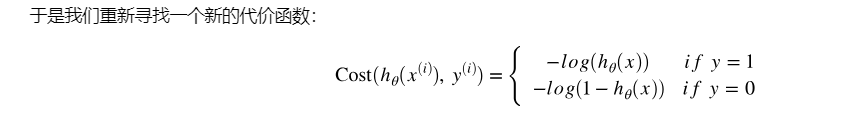
为什么是这个代价函数
之前的平方就比较好理解,现在这个形式比较像对hθ(x)这种范围适用的合理的代价函数
2.
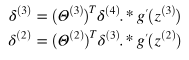
这里的求导很奇怪什么意思 -------------------------------------------- 3天后,上式表示的是损失更新,因为损失是反向算出来的,所以叫反向传播,其他参数依据此进行梯度更新。。。
这个是反向传播算法的核心,我在https://github.com/halfrost/Halfrost-Field/blob/master/contents/Machine_Learning/Neural_Networks_Learning.ipynb {二、推导}中找到了原理
本来是想过一遍推导,但发现原文有些不对劲,遂找CS229n的材料,然后发现有几个符号不清楚(迷),然后补数学去了。。。。。经过我认真思考,发现公式的逻辑有些跳。然后参考https://wenku.baidu.com/view/78046259443610661ed9ad51f01dc281e53a56cc.html 很顺畅!!!
如果不想花太多时间,数值计算的例子很好,不用这么纠结。
下面是截图:

3.数值梯度检验
双边数值法画检验图形(数值求导)一般取10-4
4.softmax
https://blog.csdn.net/bitcarmanlee/article/details/82320853 一句话:输出概率
具体有公式推导,先放放。
5.交叉熵损失函数
https://blog.csdn.net/xg123321123/article/details/52864830 看看就明白了
顺便把以前不清楚的KL散度也弄明白了
6.矩阵乘积 很烦人!
外积、Kronecker积和张量积
这里比较详细解答了 https://blog.csdn.net/zzx3163967592/article/details/88344157
7.machine learning diagnostic - 机器学习诊断法
调试算法! (重要)
数据随机排列,70%训练,其余测试。
篇幅大,先搁着。
8.以后遇到问题再说。。