图解机器学习读书笔记-CH7

最小二乘分类

本质, 分类问题用近似函数描述, 再用最小二乘法.

二分类问题: (y in {+1,-1}), 可近似定义为取值为+1, -1的二值函数问题:

预测输出(hat y):

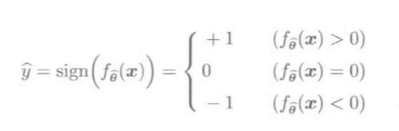
其中, (f_{hat heta}(mathbf x)=0)是小概率事件.

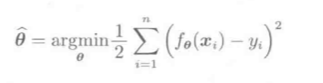
预测值(hat y)由预测结果的符号决定:

0/1损失

分类问题预测值不重要, 用符号进行模式判断, 故用0/1损失比l2损失更合适.

0/损失定义:

等价于:

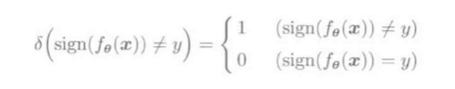
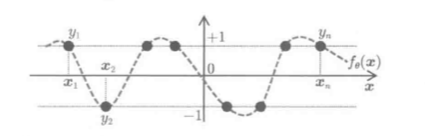
下图展示(m=f_ heta(mathbf x)y)函数的例子:

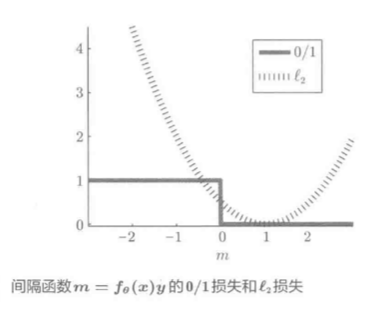
注意阶梯状的粗黑折线.

• (m>0, 损失=0, 此时f_ heta(x)和y符号相同), 对应正样本分类
• (m le 0, 损失=1, 此时两者符号不同), 对应负样本分类
• 0/1损失使用复杂模型(f_ heta(x))学习: (hat heta=underset{ heta}{min}frac{1}{2}sum_{i=1}^nleft(1-sign(f_ heta(x_i)y_i) ight))
• m尽可能大, (m_i=f_ heta(x_i)y_i)表示第i个样本的间隔

模型评估:

• 回归问题, 用L2损失评估
• 分类问题, 用代理损失计算, L2损失是相对于0/1损失的一种代理损失

因为(y^2=1), 故L2损失可用间隔函数表示:

[r^2 =(y-f_ heta(x))^2 = [y(1-frac{f_ heta(x)}{y}]^2 =y^2(1-f_ heta(x)cdot y)^2 = (1-m)^2 ]

,其中间隔函数(m=f_ heta(x)cdot y)
代理损失图示:

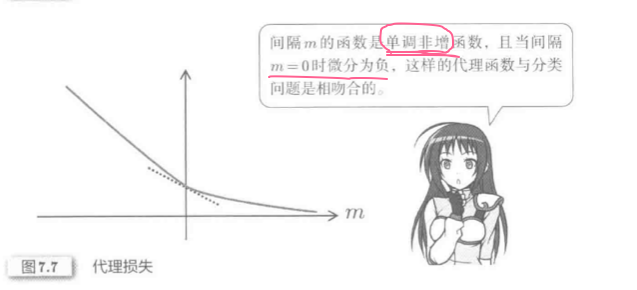
多分类

代理损失分类:

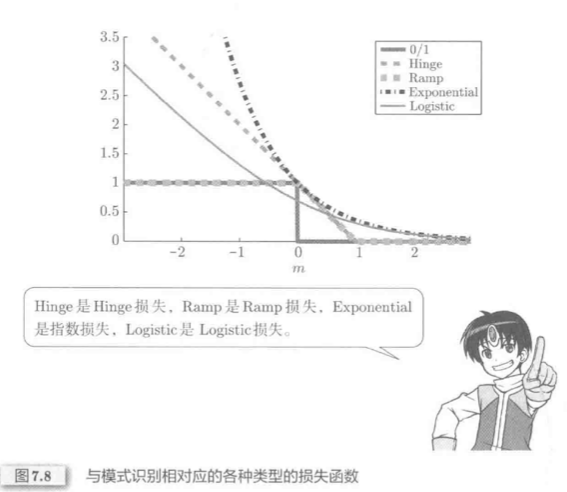
其中,

• Hinge损失对应支持向量机分类器
• Ramp损失是鲁棒学习的扩展
• 指数损失对应Boosting分类器
• Logistic损失对应逻辑回归

利用2类别模式识别算法识别多分类:

1. 一对多法
   uploading-image-952659.png

2. 一对一法