前段时间又重新回顾了线性代数的课本,感悟颇多。才渐渐体会到,大学数学课程的安排,分割为微积分、线性代数和概率论是多么的合理!
矩阵,说它多重要都不为过,尤其是大型复杂的计算。Numpy对于Python的扩展,相当程度体现在对于矩阵运算的支持上。
Example1
创建矩阵
# -*-coding:utf-8-*- import numpy as np import matplotlib.pyplot as plt
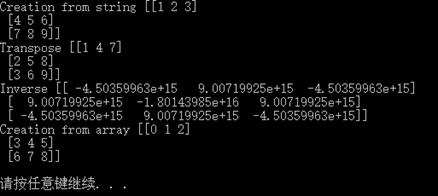
# 创建矩阵 A = np.mat('1 2 3; 4 5 6; 7 8 9') print "Creation from string", A # T属性即为转置矩阵 print "Transpose", A.T # I属性为逆矩阵 print "Inverse", A.I # 通过Numpy数组创建 print "Creation from array", np.mat(np.arange(9).reshape(3, 3)) |
结果如下:
Example2
从已有矩阵创建新矩阵
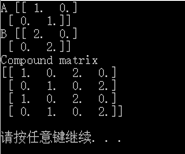
# 从已有矩阵创建新矩阵 A = np.eye(2) print 'A', A B = A * 2 print "B", B print "Compound matrix ", np.bmat("A B; A B") # 有点像分块矩阵 |
结果如下:
Example3
除法运算
# 除法运算 a = np.array([2, 6, 5]) b = np.array([1, 2, 3]) print "Divide", np.divide(a, b), np.divide(b, a) # 相当于"/" print "True Divide", np.true_divide(a, b), np.true_divide(b, a) print "Floor Divide", np.floor_divide(a, b), np.floor_divide(b, a) # 相当于"//" |
结果如下:
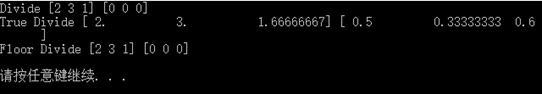
注意:这里尤为需要注意的是divide和floor divide,两者的区别在于分子分母有浮点数时的计算方式不同
Example4
模运算
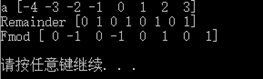
# 模运算 a = np.arange(-4, 4) print "a", a print "Remainder", np.remainder(a, 2) # 相当于"%", mod print "Fmod", np.fmod(a, 2) # fmod的区别在于处理负数的方式 |
结果如下:
Example5
创建斐波那契数列
# 创建斐波那契数列 F = np.matrix([[1, 1], [1, 0]]) # 特殊的矩阵 print "F", F print "8th Fibonacci", (F**7)[0, 0] |
结果如下:
其实很简单!
Example6
利萨如曲线
X = A sin(at+n/2)
Y = B sin(bt)
这里我们令A=B=1
# 绘制利萨如曲线 # 初始化相关参数 a = 9 b = 8 n = np.pi t = np.linspace(-np.pi, np.pi, 201) # 产生-pi~pi均匀分布的201个点 x = np.sin(a * t + n / 2) y = np.sin(b * t) plt.plot(x, y) plt.show() |
结果如下:
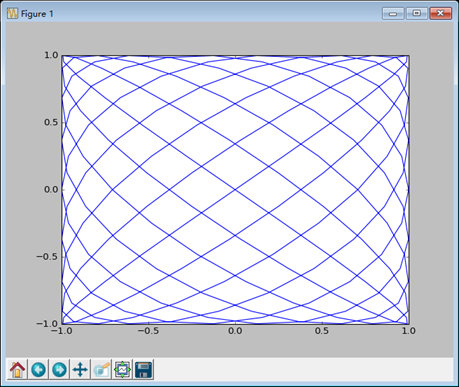
这里想要表达的是Numpy内置的函数非常的好用!
总结:这一次的练习还算简单,当然这只是入门,为接下来的工作打好基础。下一次要学习的,是Numpy中的一些经常用到的模块,不得不说,Numpy的功能的确强大,Matplotlib的制图能力亦然。
源代码:https://github.com/Lucifer25/Learn-Python/blob/master/Numpy/exercise4.py