最近一直在学HTML5和CSS3,Numpy的东西都有些生疏,那本书是已经看完了的,紧跟着相关的代码也都敲了一遍,还是发现了一些问题,因为这样的学习方式,总感觉太被动,紧紧跟着示例代码,缺少了整体观,即使你现在问我Numpy可以处理什么问题,我还是回答不出。所以,有必要回头重来一遍,再一次审视代码背后的意义,写博客真的是一个很不错的方式,毕竟,如果你不懂,写出来的文字必然也是混乱的。
那,下面记录一下Numpy学习笔记(二)
Example1
文件读写:数据不应该仅仅存在内存里,应该及时保存在硬盘上,以文件的形式
# -*- coding:utf-8 -*- # 导入numpy库 import numpy as np
# 文件读写 # 先创建一个单位矩阵 a = np.eye(2) # numpy自带的eye方法 print a # 使用savetxt函数保存 np.savetxt("D:LearnCodepythonexerciseeye.txt", a) |
结果如下:

查看相关文件夹,已经出现eye.txt,打开

Example2
CSV文件:逗号分隔值文件,很少听见,但经常遇见,用Excel打开的效果几乎与.xls文件一模一样
Numpy是用来处理数据的,而CSV是用来存储数据的,看起来渊源很深呢。
先来看一个CSV文件
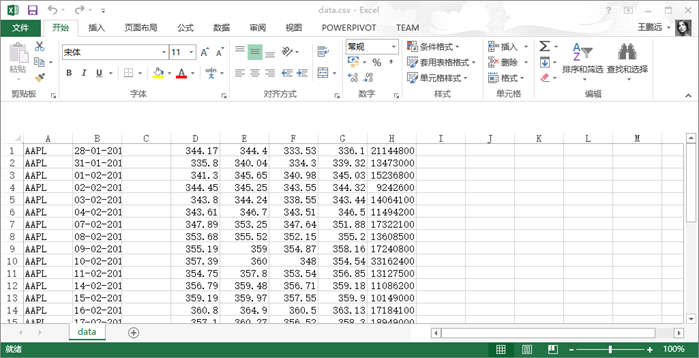
里面记录的是苹果公司的股票,第一列是股票代码,第二列是日期,第三列为空,下面依次是开盘价、最高价、最低价和收盘价和成交量
接下来我们将收盘价和成交量分别载入数组
# CSV文件 # delimiter定义分隔符,默认是空格;usecols定义选取的;unpack默认False,解包 c, v = np.loadtxt('D:LearnCodepythonexercisedata.csv', delimiter=",", usecols=(6, 7), unpack=True) print u"收盘价:", c print u"成交量:", v |
看结果:

并不困难
Example3
各种平均值的求法:书里面列举了三个,成交量加权平均价格、算术平均值、时间加权平均价格
成交量平均价格(VWAP)表示成绩量越大,该价格所占的权重就越大
算术平均值就是权重为1
时间加权平均价格(TWAP)表示日期越近的价格所占比重越大
# 成交量平均价格 c, v = np.loadtxt("D:LearnCodepythonexercisedata.csv", delimiter=",", usecols=(6, 7), unpack=True) # 计算以成交量加权的价格 vwap = np.average(c, weights=v) print "VWAP:", vwap
# 算术平均价格 mean = np.mean(c) print "Mean:", mean
# 时间加权平均价格 # 先构造一个时间序列 t = np.arange(len(c)) twap = np.average(c, weights=t) print "TWAP:", twap |
结果如下:

Example4
最大值与最小值
# 载入每日最高价和最低价的数据 h, l = np.loadtxt("D:LearnCodepythonexercisedata.csv", delimiter=",", usecols=(4, 5), unpack=True) # 直接调用max()和min()函数 print "highest:", np.max(h) print "lowest:", np.min(l)
# ptp函数可以计算取值范围 print "Spred high price:", np.ptp(h) print "Spred low price:", np.ptp(l) |
结果如下:
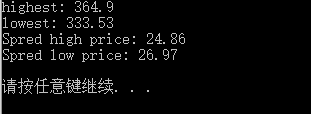
无论怎么讲都是相当便捷的
Example5
简单统计分析,这里主要是中位数、和方差
# 简单统计分析 c = np.loadtxt("D:LearnCodepythonexercisedata.csv", delimiter=",", usecols=(6, ), unpack=True) # 寻找中位数 print "median:", np.median(c) # 利用排序来检验正确与否 sorted_c = np.msort(c) print "sorted_c:", sorted_c N = len(c) if N%2 != 0: middle = sorted_c[N/2] else: middle = (sorted_c[N/2] + sorted_c[N/2-1])/2 print "middle:", middle
# 计算方差 variance = np.var(c) print "variance:", variance |
结果如下:
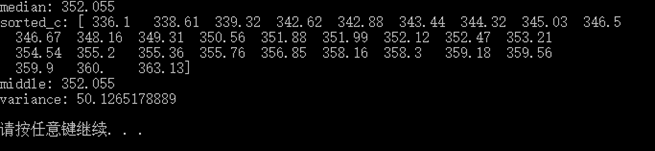
所需要的无非就只是调用个函数那么简单!
Example6
计算股票收益率,分成这么几个(都是经济学的东西,看看就好,重点还是看numpy如何使用上):简单收益率、对数收益率和波动率
# 股票收益率 c = np.loadtxt("D:LearnCodepythonexercisedata.csv", delimiter=",", usecols=(6, ), unpack=True) # 简单收益率 # diff函数返回相邻数组元素差值组成的数组 diff = np.diff(c) print "diff:", diff # 收益率等于这一天与前一天的差值除以前一天的值 returns = diff/c[:-1] print "returns:", returns # 计算收益率的标注差 print "Standard deviation:", np.std(returns)
# 对数收益率 logreturns = np.diff(np.log(c)) print "logreturns:", logreturns print "Standard deviation:", np.std(logreturns)
# 计算收益率为正值的情况 posretindices = np.where(returns > 0) print "Indices with positive returns:", posretindices
# 波动率(对数收益率的标准差除以其均值,再除以交易日倒数的平方根,交易日通常取252天) annual_volatility = np.std(logreturns)/np.mean(logreturns)/np.sqrt(1.0/252) print "Annual volatility:", annual_volatility print "Month volatility:", annual_volatility * np.sqrt(1.0/12) |
结果如下:
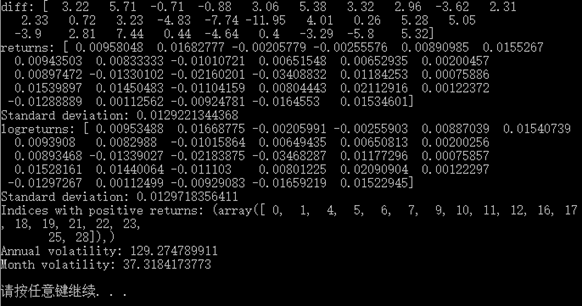
Example7
日期分析:分析CSV文件,会看到有一列日期数据,格式为dd-mm-yyyy,Python自带的时间处理模块,可以很自如地处理,而Numpy本身是无法处理这样的数据的,所以在解包的时候要先编写一个转换函数,然后将这个函数传递到loadtxt里的converters参数里
# 时间处理 # 先导入时间模块 import datetime # 编写转换函数 def datetostr(s): truetime = datetime.datetime.strptime(s, '%d-%m-%Y').weekday() return truetime # 开始读取数据,并添加converters参数 dates, close = np.loadtxt("D:LearnCodepythonexercisedata.csv", delimiter=",", usecols=(1, 6), converters={1: datetostr}, unpack=True) print "Dates:", dates # 创建一个包含五个元素的数组 averages = np.zeros(5) # where会根据条件返回满足条件的元素索引,take可以从索引中取出数据 for i in range(5): indices = np.where(dates == i) prices = np.take(close, indices) avg = np.mean(prices) print "Day", i, "prices", prices, "Average", avg averages[i] = avg |
结果是这样的:

这个练习有些困难,不仅使用到了Python里的datetime模块,还涉及到了loadtxt转换参数converters的使用,更不必说where和take了
Example8
Data.csv文件里,每一行代表每一天,如果数据量很大,我们可以考虑将它们进行压缩,按周进行汇总
# 周汇总 import datetime def datetostr(s): truetime = datetime.datetime.strptime(s, '%d-%m-%Y').weekday() return truetime dates, open, high, low, close = np.loadtxt("D:LearnCodepythonexercisedata.csv", delimiter=",", usecols=(1, 3, 4, 5, 6), converters={1: datetostr}, unpack=True) # 为了方便计算,仅取前三周数据 dates = dates[:16]
# 寻找第一个星期一 first_monday = np.ravel(np.where(dates == 0))[0] # where返回的是个多维数组,需要展平 print "First Monday", first_monday # 寻找最后一个星期五 last_friday = np.ravel(np.where(dates == 4))[-1] print "Last Friday"
weeks_indices = np.arange(first_monday, last_friday+1) print "Weeks indices initial", weeks_indices
weeks_indices = np.split(weeks_indices, 3) print "Weeks indices after split", weeks_indices
# 为了后面的apply_along_axis def summarize(a, o, h, l, c): monday_open = o[a[0]] week_high = np.max(np.take(h, a)) week_low = np.min(np.take(l, a)) friday_close = c[a[-1]] return ("APPL", monday_open, week_high, week_low, friday_close) # apply_along_axis内涵很丰富 weeksummary = np.apply_along_axis(summarize, 1, weeks_indices, open, high, low, close) print "Week summary", weeksummary # savetxt参数其实有很多 np.savetxt("D:LearnCodepythonexerciseweeksummary.csv", weeksummary, delimiter=",", fmt="%s") |
看结果:

打开文件夹,查看weekssummay.csv文件

Example9
真实波动幅度均值(ATR),这里取20天的数据
# 真实波动幅度均值 h, l, c = np.loadtxt('D:LearnCodepythonexercisedata.csv', delimiter=',', usecols=(4, 5, 6), unpack=True)
N = 20 # 切片 h = h[-N:] l = l[-N:]
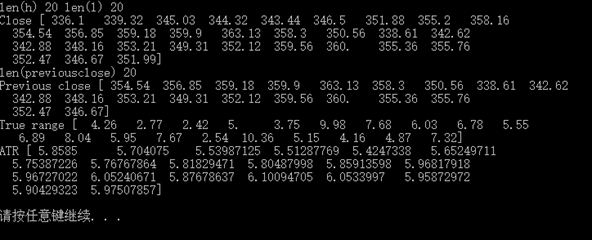
print "len(h)", len(h), "len(l)", len(l) print "Close", c # 计算前一日的收盘价 previousclose = c[-N-1:-1]
print "len(previousclose)", len(previousclose) print "Previous close", previousclose # maximum函数可以选择出每个元素的最大值 truerange = np.maximum(h-l, h-previousclose, previousclose-l)
print "True range", truerange # zeros函数初始化数组为0 atr = np.zeros(N)
atr[0] = np.mean(truerange)
for i in range(1, N): atr[i] = (N-1)*atr[i-1] + truerange[i] atr[i] /= N
print "ATR", atr |
结果是这样的
Example10
简单移动平均线
这里会涉及到一个重要的函数:consolve函数,即卷积函数。卷积的概念百度百科上是这样解释的:卷积是两个变量在某范围内相乘后求和的结果。我在知乎上看到的一个答案,说的更简洁,即加权求和。
# 简单移动平均线 # N是移动窗口的大小 N = 5 # 权重是个平均值 weights = np.ones(N) / N print "Weights", weights
c = np.loadtxt('D:LearnCodepythonexercisedata.csv', delimiter=',', usecols=(6, ), unpack=True) # 要从卷积运算中取出与原数组重叠的区域 sma = np.convolve(weights, c)[N-1:-N+1] # 生成一个时间序列 t = np.arange(N-1, len(c)) # 用matplotlib绘图 plt.plot(t, c[N-1:],'b-', lw=1.0) plt.plot(t, sma, 'r-', lw=2.0) plt.show() |
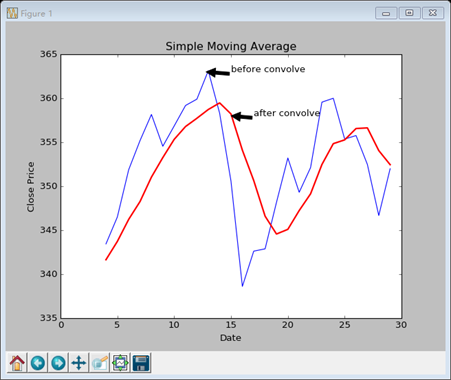
结果是这样的


Matplotlib的绘图效果相当不错,这里还可以添加一些参数
plt.xlabel("Date") plt.ylabel("Close Price") plt.title(u"Simple Moving Average") plt.annotate('before convolve', xy=(12.8, 363), xytext=(15, 363), arrowprops=dict(facecolor='black',shrink=0.005)) plt.annotate('after convolve', xy=(15, 358), xytext=(17, 358), arrowprops=dict(facecolor='black',shrink=0.005)) |
Example11
指数移动平均线
指数移动平均线使用的权重是指数衰减的,其他的与Example10一样
# 指数移动平均线 x = np.arange(5) # 对x求指数,exp函数 print "Exp", np.exp(x) # linspace函数实现等距分隔 print "Linspace", np.linspace(-1, 0 ,5) N = 5 # 上面是两个示范,下面才是真的 weights = np.exp(np.linspace(-1, 0, N)) weights /= weights.sum() print "Weights", weights
c = np.loadtxt('D:LearnCodepythonexercisedata.csv', delimiter=',', usecols=(6, ), unpack=True) ema = np.convolve(weights, c)[N-1:-N+1] t = np.arange(N-1, len(c)) plt.plot(t, c[N-1:],'b-', lw=1.0) plt.plot(t, ema, 'r-', lw=2.0) plt.show() |
结果如下


与上一幅图略有不同
Example12
布林带
股票市场的一种常用指标,基本形态是由三条轨道线组成
中轨:简单移动平均线
上轨:比简单移动平均线高两倍标准差的距离,标准差是简单移动平均线的标准差
下轨:比简单移动平均线低两倍标准差的距离,标准差是简单移动平均线的标准差
# 绘制布林带 N = 5 # 计算权重 weights = np.ones(N)/N
c = np.loadtxt('D:LearnCodepythonexercisedata.csv', delimiter=',', usecols=(6, ), unpack=True) # 简单移动平均线,注意切片 sma = np.convolve(weights, c)[N-1:-N+1] deviation = []
# 标准差为计算简单移动平均线所用数据的标准差 for i in range(0, len(c)-N+1): dev = c[i:i+N]
averages = np.zeros(N) # fill函数可以将数组元素赋为单一值,平均值恰好为sma数组里的元素 averages.fill(sma[i]) dev = dev-averages dev = dev ** 2 dev = np.sqrt(np.mean(dev)) deviation.append(dev)
# 书上的代码 ''' for i in range(N-1, len(c)): if i+N<len(c): dev = c[i:i+N] else: dev = c[-N:]
averages = np.zeros(N) averages.fill(sma[i-N-1]) dev = dev-averages dev = dev ** 2 dev = np.sqrt(np.mean(dev)) deviation.append(dev) '''
deviation = 2 * np.array(deviation) # 每个sma的元素应对应一个标注差 print len(deviation), len(sma) upperBB = sma + deviation lowerBB = sma - deviation
c_slice = c[N-1:] # 检验数据是否全都落入上轨和下轨内 between_bands = np.where((c_slice<upperBB)&(c_slice>lowerBB))
print lowerBB[between_bands] print c[between_bands] print upperBB[between_bands] between_bands = len(np.ravel(between_bands)) print "Ratio between bands", float(between_bands)/len(c_slice)
# 绘图,这个就比较简单了 t = np.arange(N-1, len(c)) plt.plot(t, c_slice, lw=1.0) plt.plot(t, sma, lw=2.0) plt.plot(t, upperBB, lw=3.0) plt.plot(t, lowerBB, lw=3.0) plt.show() |
结果如下:

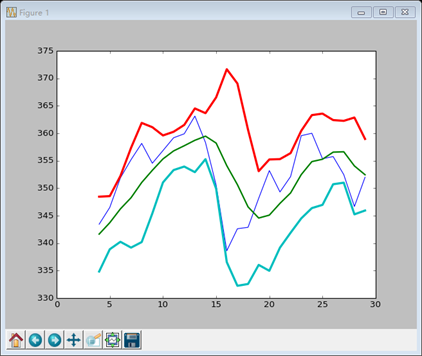
书上的代码略有不同,但我并没有看懂,而是照着自己的理解,根据布林带的规则写的,如果大家发现有什么问题,或者我的写法是错误的,希望能及时的提醒我,也好及时更改(*^_^*)
Example13
线性模型,Numpy里的linalg包是专门用来处理此类问题,今后还会接触
# 用线性模型预测价格
# 用于预测所取的样本量 N = 5
c = np.loadtxt("D:LearnCodepythonexercisedata.csv", delimiter=',', usecols = (6, ), unpack=True) # 取后N个数 b = c[-N:] # 倒序 b = b[::-1] print "b", b
# 初始化一个N*N的二维数组A A = np.zeros((N,N), float) print "Zeros N by N", A
# A[i]与b对应 for i in range(N): A[i, ] = c[-N-1-i:-1-i]
print "A", A
# lstsq函数拟合数据,返回值包括系数向量、残差数组、A的秩以及A的奇异值 (x, residuals, rank, s) = np.linalg.lstsq(A, b)
print x, residuals, rank, s
# x提供系数,dot点积即可预测下一次股价 print np.dot(b, x) |
结果如下:
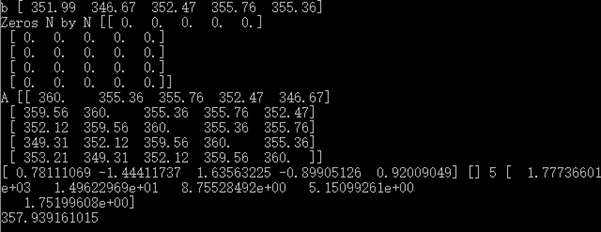
实际查得下一个交易日收盘价为353.56,说明股票市场还是很不规律的
Example14
数组的修剪和压缩
# 数组的修剪和压缩
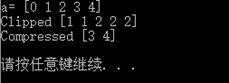
# clip返回一个修剪过的数组,小于等于给定最小值的设为给定最小值,反之亦然 a = np.arange(5) print "a=", a print "Clipped", a.clip(1, 2)
# compress返回一个给定筛选条件后的数组 print "Compressed", a.compress(a>2) |
结果也是比较明显:
Example15
阶乘
# 阶乘 b = np.arange(1, 9) print "b=", b # 一个prod()函数即可,省略了循环 print "Factorial", b.prod()
# cumprod函数可以计算累计乘积 print "Factorials", b.cumprod() |
看结果:
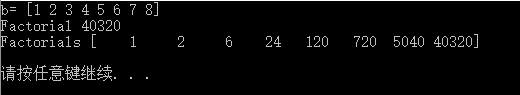
总结:从这次的笔记中可以看到,Numpy的确是很大程度上拓展了Python的统计功能,很多时候你所需要做的无非只是写个函数名,直接调用即可,Matplotlib同时提供了个性化很强的绘图功能,两者集成就可以实现很好的数据可视化。当然,这里的几个例子无非只是抛砖引玉,接下来的学习之路还很漫长。
源代码在这里:https://github.com/Lucifer25/Learn-Python/blob/master/Numpy/exercise2.py
参考资料:http://docs.scipy.org/doc/numpy/reference/
http://matplotlib.org/