郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!

ADVANCES IN NEURAL INFORMATION PROCESSING SYSTEMS 31 (NIPS 2018), (2018): 787-797
Abstract
脉冲神经元的循环网络(RSNN)是大脑惊人的计算和学习能力的基础。但RSNN模型的计算和学习能力仍然很差,至少与人工神经网络(ANN)相比是这样。我们解决了两个可能的原因。一是大脑中的RSNN不是随机连接的,也不是按照简单的规则设计的,它们也不会像一个白板网络一样开始学习。相反,大脑中的RSNN通过进化、发展和先前的经验针对其任务进行了优化。这些优化过程的细节在很大程度上是未知的。但是它们的功能贡献可以通过强大的优化方法来近似,例如随时间的反向传播(BPTT)。
大脑中的RSNN与模型之间的第二个主要不匹配是后者仅显示了大脑中神经元和突触动态的一小部分。我们在我们的RSNN模型中包含神经元,这些神经元再现了生物神经元的一个显著动态过程,该过程发生在与行为相关的秒级时间尺度上:神经元适应。我们将这些网络称为LSNN,因为它们具有长短期记忆。如果通过深度学习(BPTT与优化网络架构的重新布线算法相结合)对RSNN进行训练和配置,则包含自适应神经元将大大提高RSNN的计算和学习能力。事实上,这些RSNN的计算性能首次接近LSTM网络。此外,具有自适应神经元的RSNN可以学会学习(L2L)方案中的先前学习中获取抽象知识,并转移该知识以便从很少的示例中学习新的但相关的任务。我们在监督学习和强化学习中证明了这一点。
1 Introduction
脉冲神经元的循环网络(RSNN)经常被研究为大脑中神经元网络的模型。原则上,它们应该特别适合时域中的计算,例如语音处理,因为它们的计算是通过脉冲(即时间和空间中的事件)进行的。但是对于时序处理任务,RSNN模型的性能仍然不是最理想的。大脑中的RSNN和RSNN模型之间的一个区别是,大脑中的RSNN通过长期的进化过程对其功能进行了优化,并在开发过程中辅以复杂的学习课程。由于这些生物过程的大部分细节目前仍然未知,我们询问深度学习是否能够在RSNN模型的功能级别上模拟这些复杂的优化过程。我们使用BPTT作为网络优化的深度学习方法。反向传播之前已经适用于[1, 2]中具有二值激活的前馈网络,并且我们将BPTT调整为以类似的方式适用于RSNN。为了同时优化RSNN的连接性,我们使用DEEP R(这是一种受生物学启发的突触重新布线启发式算法[3, 4])增强了BPTT。与LSTM网络相比,RSNN的短期记忆能力往往较差。由于大脑中的神经元在大于几十毫秒的时间尺度上配备了许多动态过程[5],因此我们通过标准的神经适应过程丰富了模型中神经元的固有动态。
我们首先展示(第4节),这种方法为两个常见的基准任务:Sequential MNIST和TIMIT(语音处理任务)产生了新的RSNN计算性能水平。然后我们证明它使L2L适用于RSNN(第5节),类似于LSTM网络。特别是,我们展示了meta-RL [6, 7]产生了RSNN的新电机控制能力(第6节)。该结果将最近用于大脑中基于奖励的学习的抽象模型[8]与脉冲活动联系起来。此外,我们展示了具有稀疏连通性和10-20 Hz的稀疏发放活动的RSNN(参见图1D、2D、S1C)可以解决这些任务和其他任务。因此,这些RSNN使用脉冲而不是发放率进行计算。
LSNN卓越的计算和学习能力表明,它们对于在基于脉冲的神经形态芯片(如Brainscales [9]、SpiNNaker [10]、True North [2]、来自ETH Zürich [11]的芯片和Loihi [12])中的实现也很感兴趣。特别是,诸如反向传播之类的非局部学习规则对于其中一些神经形态设备(以及许多大脑模型)来说是挑战。因此,需要用于非线性函数的RSNN学习的替代方法。我们在第5节和第6节中展示了L2L可用于生成即使在没有突触可塑性的情况下也能非常有效地学习的RSNN。
Relation to prior work: 我们参考[13, 14, 15, 16]来总结先前关于RSNN计算能力的结果。那里的重点通常是动态模式的生成。本文未涉及此类任务,但将在[17]中显示LSNN为生成复杂的时间模式提供了[16]的替代模型。Huh et al. [15]将梯度下降应用于脉冲神经元的循环网络。在那里,使用了没有泄漏的神经元。因此,神经元的电压可以在该方法中用于在无限长的时间内存储信息。
我们不知道以前尝试将RSNN的时间序列分类性能纳入LSTM网络的性能范围。我们也不知道以前有任何关于将L2L应用于SNN的文献。
2 LSNN model
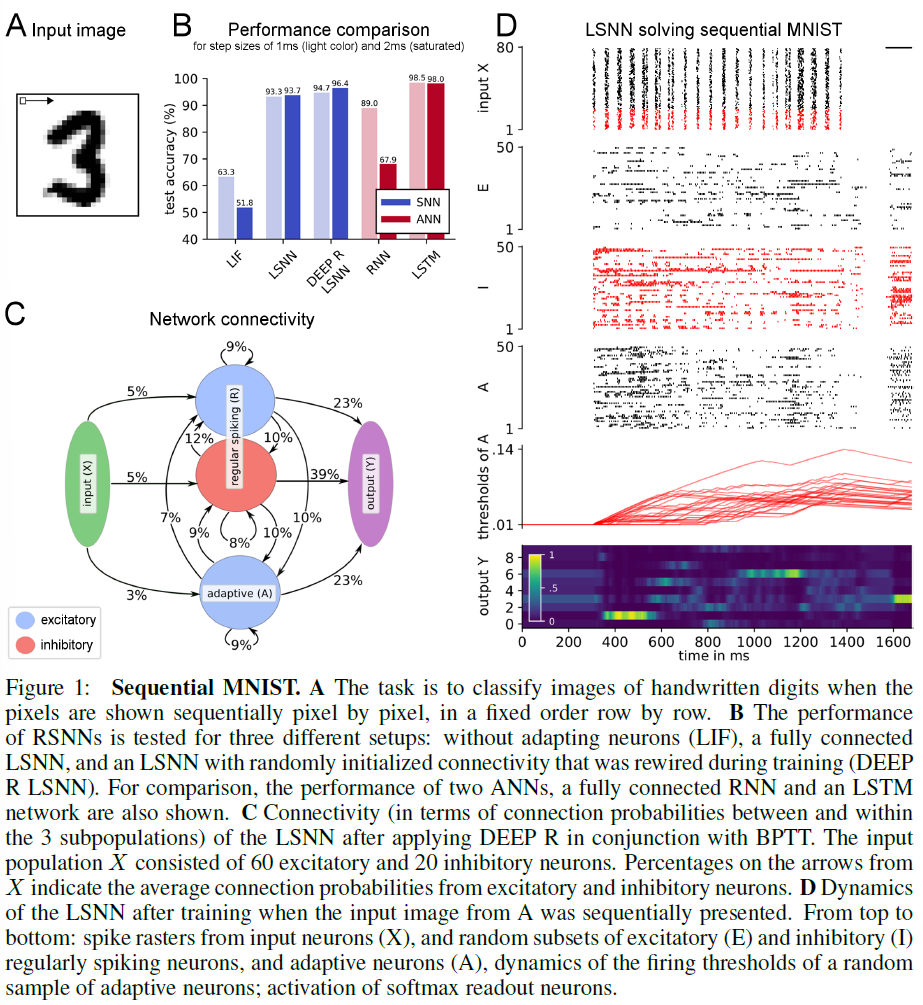
常见RSNN模型中的神经元和突触缺少在其生物学对应物中发现的许多动态过程,尤其是在较大时间尺度上的动态过程。我们将其中之一整合到我们的RSNN模型中:神经元适应。众所周知,大脑中很大一部分兴奋性神经元正在适应,具有不同的时间常数,参见例如Allen脑图谱,用于获取来自小鼠和人类新皮质的数据。我们将由此产生的RSNN类型称为长短期记忆脉冲神经网络(LSNN)。LSNN由一个LIF神经元(兴奋性和抑制性)群体R和另一个LIF兴奋性神经元群体A组成,其兴奋性通过之前的激发活动暂时降低,即这些神经元正在适应(见图1C和增刊)。群体R和A都接收来自外部输入神经元群体X的脉冲序列。计算结果由外部线性读出神经元群体Y读出,见图1C。
[18,19,20,21]中描述了拟合模型以使神经元适应数据的常用方法。我们在这里使用了可以说是最简单的模型:我们假设神经元 j 的发放阈值Bj(t)对于这个神经元 j 的每个脉冲都会增加某个固定量β/τa,j,然后指数衰减回基线值![]() 具有时间常数τa,j。因此,δt = 1 ms的离散时间步长的阈值动态如下所示:
具有时间常数τa,j。因此,δt = 1 ms的离散时间步长的阈值动态如下所示:
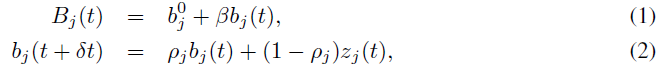
其中![]() 和zj(t)是神经元 j 的脉冲序列,假设值为{0, 1/δt}。请注意,自适应脉冲神经元的阈值动态类似于[22]中上下文神经元状态的动态。通常将适应神经元的时间常数置于短期记忆所需的范围内就足够了(有关每个实验中使用的特定值,请参见增刊)。
和zj(t)是神经元 j 的脉冲序列,假设值为{0, 1/δt}。请注意,自适应脉冲神经元的阈值动态类似于[22]中上下文神经元状态的动态。通常将适应神经元的时间常数置于短期记忆所需的范围内就足够了(有关每个实验中使用的特定值,请参见增刊)。
3 Applying BPTT with DEEP R to RSNNs and LSNNs
我们优化了突触权重,在某些情况下还优化了LSNN的连接矩阵,用于特定范围的任务。我们使用的优化算法,即时间反向传播(BPTT),并没有声称在生物学上是合理的。但与进化和发展过程一样,BPTT可以针对特定任务范围优化LSNN。反向传播(BP)已在[1]和[2]中应用于脉冲神经元的前馈网络。在这些方法中,梯度通过脉冲反向传播,方法是将脉冲时不存在的膜电位导数替换为从0到1平滑增加,然后衰减回0的伪导数。我们减少了("阻尼")伪导数的幅度小于1(详见补充材料)。这提高了在较大时间跨度内计算的RSNN的BPTT性能,这需要通过几个1000层展开的脉冲神经元前馈网络进行反向传播。在[15]中提出了一种类似的用于RSNN的BPTT实现。目前尚不清楚这两个版本的BPTT中哪一个最适合给定任务和给定网络。
为了不仅优化RSNN的突触权重,还优化其连接矩阵,我们将BPTT与受生物学启发的[3]重新布线方法DEEP R [4]相结合(详见增刊)。DEEP R通过不断更新活动连接集[23, 3, 4]在理论上收敛到最佳网络配置。

4 Computational performance of LSNNs
Sequential MNIST:
Speech recognition (TIMIT):
5 LSNNs learn-to-learn from a teacher
RSNN模型的学习能力仍然相当差的一个可能原因是,通常需要一个白板RSNN模型来学习。相比之下,大脑中的RSNN已通过一系列先前的过程(从进化到相关任务的先前学习)对其学习性能进行了优化。我们使用L2L设置为RSNN模拟类似的训练范例。我们在这里仅探讨L2L对LSNN的应用,但L2L也可以在不调整神经元的情况下应用于RSNN [27]。L2L对LSNN的应用很诱人,因为L2L最常用于机器学习中的ANN对应:LSTM网络参见例如[6, 7]。LSTM网络特别适用于L2L,因为它们可以容纳两个级别的学习和学习洞察力的表示:突触连接和权重可以在更高的级别上编码学习算法和大时间范围内的先验知识。LSTM网络的短期记忆可以在当前学习任务期间在较低的学习水平上积累知识。最近有人认为[8]前额叶皮层(PFC)在其短期记忆中类似地在基于奖励的快速学习过程中积累知识,而不使用多巴胺门控突触可塑性,见8]中的增刊图3。[28]的实验结果还表明,短期记忆在运动皮层的快速学习中具有突出的作用。
L2L的标准设置涉及一个大的(实际上通常是无限大的)学习任务C族F。学习在两个循环中同时进行(见图2A)。内循环学习涉及通过神经网络N(在我们的例子中是LSNN)对单个任务C的学习。N的一些参数(称为超参数)在外循环优化中进行了优化,以支持从F中快速学习随机抽取的任务C。外循环训练——在这里通过BPTT实现——在比内循环大得多的时间尺度上进行循环,整合来自族F的许多不同任务C的性能评估。可以将这个外部循环解释为一个模拟进化和发育优化过程以及先前学习对大脑网络学习能力的影响的过程。我们可以互换使用术语训练和优化,但术语训练对我们模拟的长期进化过程的描述较少。就像在[29, 6, 7]中一样,我们让N的所有突触权重属于通过外循环优化的超参数集。因此,网络被迫对学习当前任务C在其内部状态中的所有结果进行编码,特别是在其发放活动和适应神经元的阈值中。因此,神经网络N的突触权重可以自由地编码一种有效的算法,用于从F中学习任意任务C。
当大脑学会预测感官输入或动作导致的状态变化时,这可以形式化为向老师学习(即监督学习)。在这种情况下,老师是环境,它提供——通常有一些延迟——网络的目标输出。[29]的L2L结果表明,LSTM网络可以从老师那里学习非线性函数,而无需修改其突触权重,而是使用它们的短期记忆。我们询问LSNN是否也可以实现这种形式的学习。
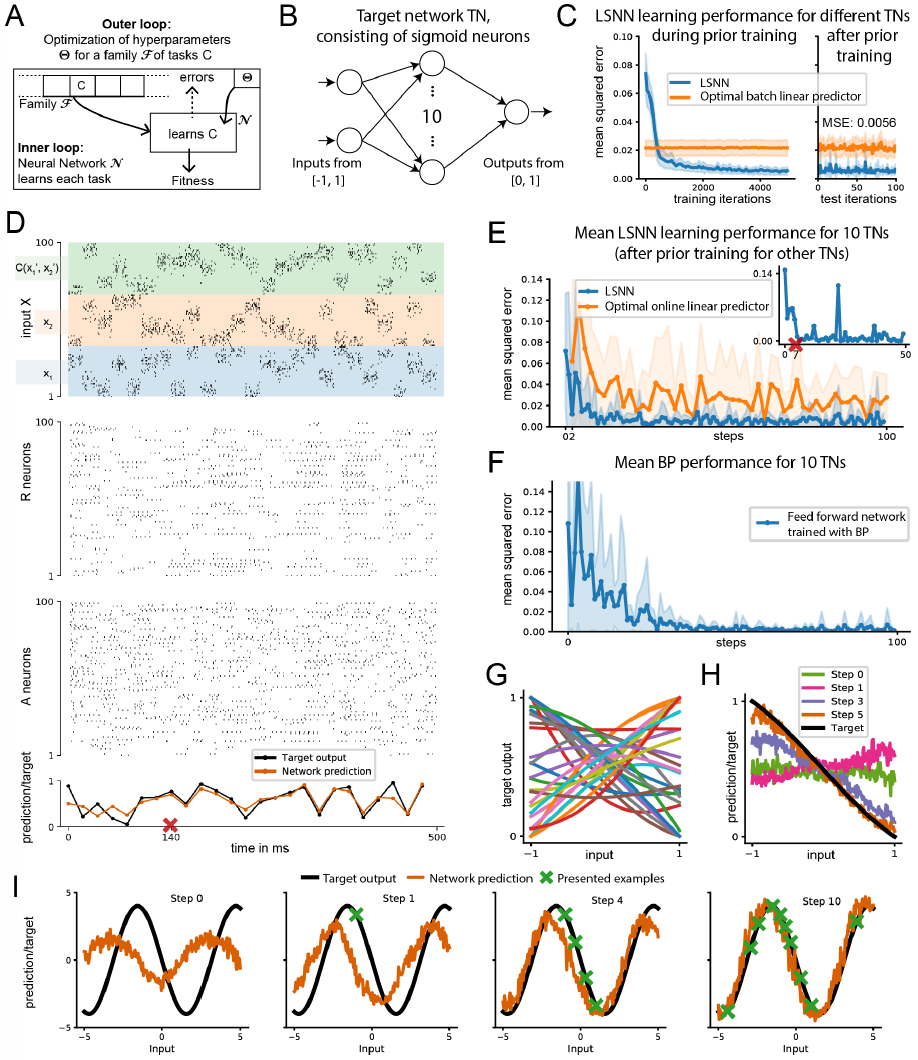
Task: 我们考虑了从老师那里学习复杂非线性函数的任务。具体来说,我们选择了两个实值变量(x1, x2)的一类连续函数作为任务族F。此类被定义为所有函数的族,它们可以由2层sigmoidal神经元人工神经网络计算,隐藏层中有10个神经元,权重和偏差来自[-1, 1],见图2B。因此,总体而言,来自F的每个此类目标网络(TN)都是通过[-1, 1]范围内的40个参数定义的:30个权重和10个偏差。我们将教师输入提供给LSNN,以便以延迟的方式从F中学习特定的TN C,如[29]:在N为先前输入提供其猜测的输出值之后给出目标输出值。
反馈的这种延迟与生物学上合理的情况是一致的。同时,反馈的延迟可以防止N在没有首先自己产生预测的情况下将教师值作为输出传递。
Implementation: 我们考虑了一个LSNN N,它由180个定期发放的神经元(群体R)和120个适应神经元(群体A)组成,适应时间常数的分布在1到1000毫秒之间均匀采样并具有完全连接性。在这种情况下,稀疏连接与重新布线并没有提高性能。LSNN中的所有神经元都接收来自300个外部输入神经元的群体X的输入。线性读数接收来自R和A中所有神经元的输入。LSNN接收3种外部输入流(参见图2D的顶行):x1、x2和输出![]() 的值)的TN用于前面的输入对
的值)的TN用于前面的输入对![]() (在第一次试验中设置为0),所有这些都通过100个脉冲神经元的外部群体中的群体编码来表示。它在20 ms窗口期间从网络中的所有神经元产生加权脉冲计数形式的输出(参见图2D的底行),其中该线性读数的权重被训练,就像LSNN内的所有权重一样,在外部循环,并在学习特定TN期间保持固定。
(在第一次试验中设置为0),所有这些都通过100个脉冲神经元的外部群体中的群体编码来表示。它在20 ms窗口期间从网络中的所有神经元产生加权脉冲计数形式的输出(参见图2D的底行),其中该线性读数的权重被训练,就像LSNN内的所有权重一样,在外部循环,并在学习特定TN期间保持固定。
L2L外循环的训练过程如下:网络训练分为训练集。在每个训练集开始时,随机选择一个新的目标网络TN,并用于为随机选择的输入对(x1, x2)生成目标值C(x1, x2) ∈ [0, 1]。这些输入对和目标中的500个被用作训练数据,并在回合中每一步向LSNN呈现一个,其中每一步持续20毫秒。使用BPTT更新LSNN参数,以最小化LSNN输出和训练集中目标之间的均方误差,使用在10个此类事件的批上计算的梯度,形成外循环的一次迭代。换句话说,每次权重更新都包括对来自10个不同TN的输入/目标对计算的梯度。这种训练过程迫使LSNN以支持学习许多不同TN的方式调整其参数,而不是专门预测单个TN的输出。训练后,LSNN的权重保持不变,需要通过仅使用其短期记忆和动态以在线方式从F中学习以前从未见过的TN的输入/输出行为。请参见增刊以了解更多详情。
Results: 由来自F类的TN计算的大多数函数都是非线性的,如图2G所示,对于x1 = x2的输入(x1, x2)的情况。因此,使用生物学上合理的局部可塑性机制学习任何此类TN的输入/输出行为对SNN来说是一项艰巨的挑战。图2C显示,在外循环中进行数千次训练迭代后,LSNN在从F族学习新的TN时实现了低MSE,显著超过了在所有500对输入和目标输出上训练的最优线性逼近器(线性回归)的性能,参见图2C, E中的橙色曲线。鉴于每个TN由40个参数定义这一事实,令人惊讶的是,用于学习新TN的输入/输出行为的LSNN网络学习算法通常会在刚刚5到20个试验,在每个试验中呈现一个随机抽取的标记示例。通用学习过程的一个示例如图2D所示。每个示例序列都会唤起一个内部模型,该模型存储在 LSNN 的短期记忆中。图2H显示了在第一次试验期间TN的LSNN内部模型的快速演变(可视化为2D输入空间的1D子集)。我们通过对域中均匀间隔点(x1, x2)的假设新输入的预测C(x1, x2)探查LSNN的当前内部模型(不允许它修改其短期记忆;所有其他输入根据LSNN的动态推进网络状态)。可以看到,LSNN的内部模型从一开始就是一个平滑函数,与F中的TN定义的类型相同。在几次试验中,这个平滑函数非常接近TN。因此,LSNN在L2L外循环的训练期间已经获得了要学习的函数类型的先验,该函数类型被编码在其突触权重中。这个先验实际上非常有效,因为图2E和F表明LSNN能够通过比在人工神经网络中直接学习TN的通用学习算法更少的试验来学习TN,如图2A所示:BP具有偏爱小权重和偏差的先验(参见补充中第3节的结尾)。这些结果表明L2L能够在LSNN中安装某种形式的关于任务的先验知识。我们推测LSNN将平滑函数的内部模型拟合到它收到的示例。
我们在第二个更简单的L2L场景中测试了这个猜想。在这里,族F由具有任意相位和幅度在0.1和5之间的所有正弦函数组成。图2I显示LSNN在该设置中还通过外循环训练获得了一个用于正弦函数的内部模型(类似于图2H所示)。即使我们以对抗的方式选择样本,恰好在一条直线上,这也不会干扰LSNN的先验知识。
总而言之,从学习算法设计的角度来看,通过L2L在LSNN中诱导的网络学习特别令人感兴趣,因为我们不知道以前记录的用于安装结构先验以在线学习脉冲神经元循环网络的方法。
6 LSNNs learn-to-learn from reward
我们现在转向元强化学习(meta-RL)在LSNN中的应用。在元强化学习中,LSNN接收奖励而不是教师输入。Meta-RL为LSTM网络带来了许多显著的结果,参见例如[6, 7]。此外,[8]表明元强化学习为大脑中基于奖励的学习提供了一个非常有趣的视角。我们专注于[6]和[7]中更具挑战性的演示之一,其中智能体必须学习在2D竞技场中找到目标,并随后从竞技场中的随机位置导航到该目标。该任务与著名的Morris水迷宫任务[30, 31]的生物学习范式有关。我们在这里研究智能体从任务的具体设置中发现两条抽象知识的能力:目标位置的分布,以及目标位置在每一个回合内是恒定的这一事实。我们询问智能体是否能够利用从学习中获得的抽象知识片段来处理许多具体的回合,并使用它来更有效地导航。
Task: 一个基于LSNN的智能体接受了一系列导航任务的训练,这些任务在圆形舞台上具有连续的状态和动作空间。该任务由一系列回合构成,每个回合持续2秒。目标是在竞技场边界上的每一回合随机放置的。当智能体达到目标时,它会获得1的奖励,并被随机放回竞技场。当智能体撞墙时,它会收到-0.02的负奖励,并且速度向量被截断以保持在竞技场内。目标是最大回合中达到的目标数量。这个任务族F由无限的可能目标位置集定义。对于每一个回合,一个最优的智能体应该探索直到它找到目标位置,记住它并利用这个知识,直到回合结束,通过最短路径到达目标。 我们训练了一个LSNN,以便网络可以在不改变其网络权重的情况下控制智能体在所有任务中的行为。
Implementation: 由于只有几百个神经元的LSNN无法处理视觉输入,我们通过像高斯群体发放率编码的当前位置的位置单元提供了智能体在竞技场内的当前位置。缺乏视觉输入使得沿着平坦的路径移动或与墙壁保持安全距离已经具有挑战性。智能体以来自外部神经元的脉冲形式接收有关正和负奖励的信息。对于外循环中的训练,我们将BPTT与DEEP R一起用于近端策略优化(PPO)算法[32]的智能体目标。在这项任务中,LSNN有400个循环单元(200个兴奋性神经元、80个抑制性神经元和120个自适应神经元,适应时间常数τa为1200 ms),网络以20%的固定连接重新连接。生成的网络图和脉冲栅格显示在增刊图1。
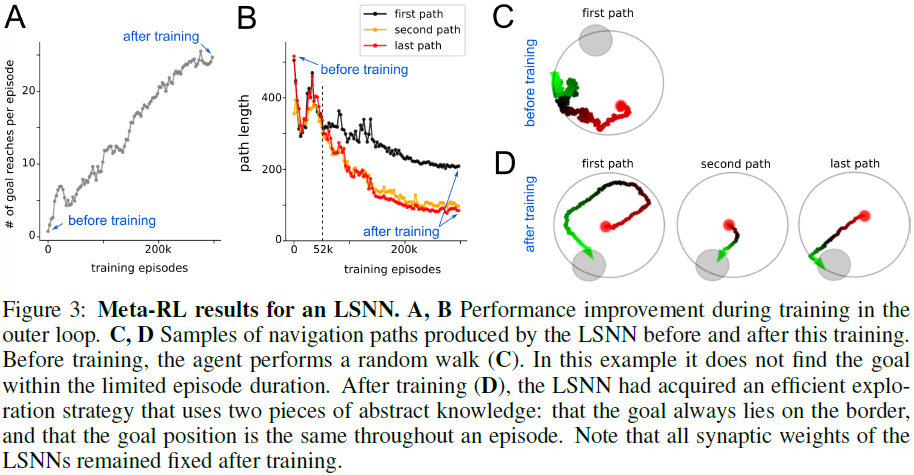
Results: L2L优化之前、期间和之后的网络行为如图3所示。图3A表明,大量的训练集最终提供了显著的改进。仔细观察图3B,可以看到在52k训练集之前,中间路径规划策略似乎没有使用发现的目标位置来缩短后续路径。因此,智能体还没有发现目标位置在一个回合中没有改变。在训练了300k回合之后,从图3D中的示例路径中可以看出,这两条抽象知识都已被智能体发现。图3D中的第一条路径显示智能体利用目标位于迷宫的边界。第二条也是最后一条路径表明智能体知道该位置在整个回合中是固定的。总而言之,这个演示表明meta-RL可以应用于RSNN,并产生以前从未见过的稀疏发放RSNN的能力,以从实验中提取抽象知识,并以巧妙的方式使用它来控制行为。
7 Discussion
我们已经证明,深度学习为研究脉冲神经网络提供了一种有用的新工具:它允许我们为具有增强计算和学习能力的RSNN创建架构和学习算法。为了证明这一点,我们调整了BPTT,使其对RSNN有效工作,并且可以与受生物学启发的突触重新布线方法(DEEP R)相结合。我们在第4节中表明,这种方法允许我们创建稀疏连接的RSNN, 接近LSTM网络在用于时空模式分类(序列MNIST和TIMIT)的常见基准任务上的性能。RSNN计算能力的这种质的飞跃是通过在模型中引入自适应神经元来支持的。根据[33],自适应神经元将较长时间常数的扩展引入RSNN,就像它们在新皮层中所做的那样。我们将由此产生的RSNN模型变体称为LSNN,因为由此产生的短期记忆能力更长。从SNN的能量效率的角度来看,这种形式的短期记忆特别有趣,因为它通过不发放神经元来存储和传输存储的信息:在其增加的发放阈值中保存信息的神经元往往会较少发放。
我们在图2中表明,深度学习(BPTT和DEEP R)在L2L的外循环中的应用为RSNN学习非线性输入/输出映射提供了新的范例。这个学习任务被认为需要在RSNN中实现BP。我们已经证明它不需要BP,甚至不需要改变突触权重。此外,我们已经证明,这种新形式的网络学习使RSNN在经过L2L外循环中类似学习任务的适当训练后,能够更快地从同一类学习新任务。原因是先前的深度学习已经在RSNN中安装了关于这些学习任务的共同属性的抽象知识(先验)。据我们所知,迁移学习能力和先验知识的使用(见图2I)以前没有在SNN中得到证明。图3显示L2L还包含RSNN从奖励中学习的能力(元强化学习)。例如,它使RSNN(无需任何额外的外部控制或时钟)能够体现一个智能体,该智能体首先在竞技场中搜索目标,然后利用所学知识从随机初始位置快速导航到该目标。在此,为了简单起见,我们只考虑了更常见的情况,即所有突触权重都由L2L的外循环确定。但是,当仅在外循环中学习一些突触权重时,会出现类似的结果,而其他突触使用局部突触可塑性规则来学习当前任务[27]。
总而言之,我们期望我们引入的新方法和想法将促进我们对大脑中RSNN的理解和逆向工程。例如,图1-3中出现的RSNN都通过类似大脑的稀疏发放活动进行计算和学习,这与使用发放率代码操作的SNN完全不同。此外,这些RSNN提出了短期记忆的新功能用途,远远超出了[34]中记住先前输入的范围,并提出了新形式的活动静默记忆[35]。
除了对计算神经科学的这些影响之外,我们发现RSNN可以通过非常节能的稀疏发放活动获得强大的计算和学习能力,这为基于脉冲的计算硬件通过非发放提供了新的应用范例。
Supplementary information for: Long short-term memory and learning-to-learn in networks of spiking neurons
我们在本补充文件中提供了有关正文的模型和模拟的详细信息,根据其中的相应部分进行结构化。
2 LSNN model


3 Applying BPTT with DEEP R to RSNNs and LSNNs


4 Computational performance of LSNNs
5 LSNNs learn-to-learn from a teacher
6 LSNNs learn-to-learn from reward