郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!

bioRxiv, November 20, 2021
Abstract
生物学习在多个相互关联的时间尺度上运作,从漫长的进化延伸到个人生命的相对较短的时间跨度。虽然在脉冲神经网络(SNN)的背景下,每个过程都被单独模拟为基本学习算法,但两者的集成仍然有限。在这项研究中,我们首先使用单个模型学习分别训练SNN,使用脉冲时序依赖强化学习(STDP-RL)和进化(EVOL)学习算法来解决CartPole强化学习(RL)控制问题。然后,我们开发了一种受生物进化启发的交错算法,该算法按顺序结合了EVOL和STDP-RL学习。
我们使用带有NetPyNE的NEURON模拟器来创建与OpenAI的Gym的CartPole环境接口的 SNN。在CartPole中,目标是通过在1-D平面上向左/向右移动来平衡垂直杆。我们的SNN包含组织成三层的多个神经元群:感觉层、关联/隐藏层和运动层,其中神经元通过兴奋性(AMPA/NMDA)和抑制性(GABA)突触连接。关联层和运动层包含一个兴奋性(E)群体和两个具有不同突触时间常数的抑制性(I)群体。每个神经元都是一个基于事件的IF模型,兴奋性神经元之间具有可塑性连接。在我们的SNN中,环境会激活根据游戏状态的特定特征进行调整的感觉神经元。我们将运动群体分成代表每个运动选择的子集。在一个时间间隔内具有更多脉冲的子集决定了动作。
在STDP-RL期间,我们通过判断移动的有效性(例如,将CartPole移动到平衡位置)来提供每个动作的中间评估(奖励/惩罚)。在EVOL期间,更新包括将连接权重的许多随机扰动加在一起。每组随机扰动都由它在独立应用时获得的总回合奖励加权。我们在训练后评估每种算法的性能,并通过创建感觉/运动动作图来描述网络将感觉输入转换为高阶表征和最终运动决策的过程。EVOL和STDP-RL训练都产生能够左右移动推车并保持杆垂直的SNN。与独立运行的STDP-RL和EVOL算法相比,我们的交错训练范式提高了性能的鲁棒性,通过对感觉/运动映射的分析揭示了不同的策略。突触权重矩阵的分析还分别显示了在EVOL和STDP-RL算法之后的分布式与集群表示。这些权重差异也表现为扩散与同步发放模式。我们的建模为RL中的SNN开辟了新的能力,可以作为神经生物学家的测试平台,旨在了解神经元回路中的多时间尺度学习机制和动力学。
Keywords
Reinforcement learning, evolution, spiking neuronal networks, computer simulation
Introduction
进化变化和个体一生中的变化发生在截然不同的时间尺度上,通过不同但相互作用的机制(Feldman, Aoki and Kumm, 1996; Parisi et al., 2019)。当个体足够健康以产生后代时,将他们的基因传给下一代时,进化就会成功(Garrett, 2012)。虽然个体学习仅限于动物的生命周期,但它仍然具有强大的竞争优势。这反过来又促进了进化过程:了解环境特性(包括其威胁和奖励)的动物更有可能生存和繁殖。此外,基因组瓶颈会阻止对动物基因组中的所有相关环境信息进行编码(Zador, 2019; Koulakov, Shuvaev and Zador, 2021)。由于所有这些原因,为了生存而学习也必须在个人层面上进行。
以前,进化和个体学习的计算机模型已被用于单独研究这两个过程的动力学和机制(Rumbell et al., 2016; Farries and Fairhall, 2007)。然而,两者之间的相互作用尚未得到广泛研究,特别是在脉冲神经元网络(SNN)的背景下。在这里,我们使用感觉和运动电路的SNN来研究这些具有不同时间尺度的受生物学启发的算法在动态环境中学习行为的有效性。我们将个体建模为SNN,这些SNN使用脉冲时序依赖强化学习(STDP-RL)进行学习,这是一种以前用于训练SNN执行行为的方法(Anwar et al., n.d.; Patel et al., 2019; Hazan et al., 2018; Chadderdon et al., 2012)。STDP-RL修改突触权重以推动个人在其环境中更优化地执行行为。在更长的时间尺度上,我们使用进化策略算法(EVOL)(Salimans et al., 2017)的一个版本,该算法在训练ANN以解决复杂的控制问题方面是有效的。在生物学背景下,EVOL将突触权重视为个体的基因组。然后EVOL使用突变遗传算子扰乱基因组以产生后代。然后这些后代与环境相互作用以评估它们的适应性。然后EVOL对后代基因组进行遗传组合,每个基因组都根据其相应的相对环境适应性进行加权。然后这个过程不断迭代,随着时间的推移提高性能。
我们首先分别研究这两种学习算法,比较CartPole常用控制问题的性能,其目标是在可以在每个时间步骤向左或向右移动的推车上垂直平衡一根杆。这两种算法都成功地训练了我们的SNN模型,并在权重矩阵中产生了非常不同的模式,EVOL之后具有更多的分布式表征,而STDP-RL之后具有更多的聚类。我们在训练后评估每种算法的性能,并为运动输出图创建不同的感官输入,以展示每个网络对学习和决策能力的保留。之后,我们研究了一种按顺序结合STDP-RL和EVOL的交错算法。这种与实际生物和个体学习并行的顺序算法展示了卓越的性能,增强了对初始条件的鲁棒性并提高了稳定性。我们的建模提供了一套用于训练SNN的新算法,它们在生物学习的时间尺度上架起了桥梁,并可以阐明体内的学习机制。
Materials and Methods
CartPole Game
Simulations
Constructing a spiking neuronal network model to play CartPole
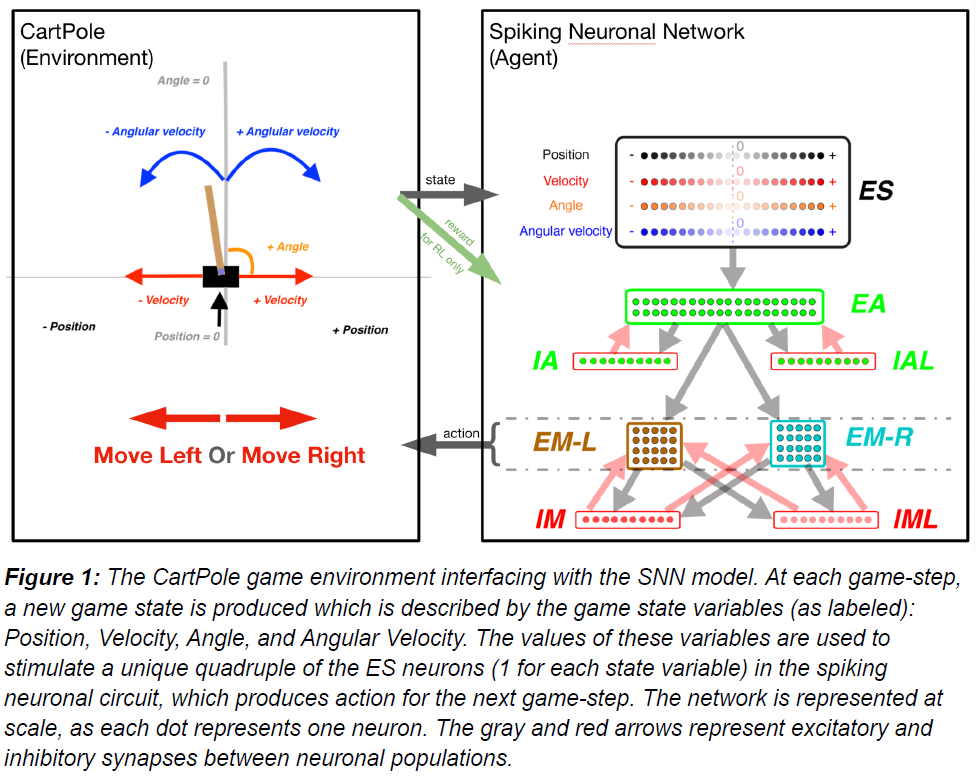
为了使SNN模型能够可靠地捕捉游戏状态空间,我们在感觉区(ES)中包含了80个神经元,每个神经元有四个子群(每个子群20个),每个子群对位置、速度、角度和角速度进行编码(图1B)。每个神经元被分配一个不同的感受野。由于游戏的目标是平衡杆,这就要求在平衡状态附近对感官信息进行更精确的编码。当失去平衡时,即游戏状态变量偏离更大的值,事件结束,需要对这些极值进行不太精确的编码。为了在平衡状态下利用较小的感受野获得较高的感官精确度,而在外围利用较大的感受野获得较低的精确度,我们根据高斯分布的百分位数将感受野分配给每个神经元,以第11个神经元为中心的峰值为0,因此当我们移动到较低的神经元指数时,它以降序表示状态变量的负值。当我们移动到更高的神经元指数时,它以递增的顺序表示状态变量的正值。所有四个ES群体均使用高斯分布和每个输入状态的期望均值和方差分配感受野。
在每个游戏步骤中,每个子群中的4个ES神经元被激活,通知SNN模型有关游戏状态的信息。为了允许代表游戏状态的各个状态变量之间的关联,我们在关联区域(EA)中包含了40个神经元,该区域接收来自ES群体的输入。EA中的每个神经元都连接到运动区域EM-L和EM-RL,通过比较这些群体中的脉冲数量(赢家通吃)产生左右动作。如果两个子群具有相同数量的脉冲,则执行随机移动。
为了防止过度兴奋和去极化阻滞(Anwar et al., n.d.; Chadderdon et al., 2012; Neymotin et al., 2013),我们纳入了抑制性神经元群(10 IA、10 IAL、10 IM和10 IML)。
Integrate-and-Fire neuron
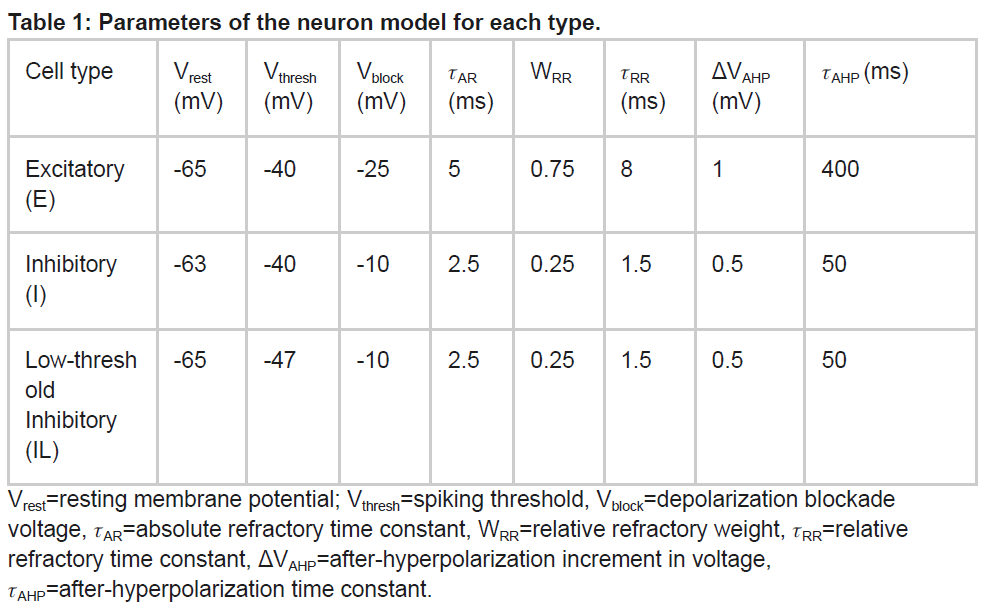
单个神经元被建模为事件驱动、基于规则的动态单元,具有在真实神经元中发现的许多关键特征,包括适应、爆发、去极化阻断和电压敏感的NMDA电导(Lytton et al., 2008; Lytton and Stewart, 2006; Neymotin et al., 2011)。事件驱动处理为网络集成提供了一种更快的替代方案:突触前脉冲是在突触后神经元延迟后到达的事件;这种到达然后是触发突触后神经元进一步处理的后续事件。神经元被参数化(表1)为兴奋性(E)、快速脉冲抑制(I)和低阈值激活抑制(IL)。每个神经元都有一个膜电压状态变量(Vm),基准值由静息膜电位参数(Vrest)确定。在突触输入事件之后,如果Vm超过脉冲阈值(Vthresh),细胞将发放动作电位并进入绝对不应期,持续AR ms。动作电位后,超极化后电压状态变量(VAHP)增加固定量ΔVAHP,然后从Vm中减去VAHP。然后VAHP呈指数衰减(时间常数为AHP)到0。为了模拟去极化阻滞,如果Vm超过阻滞电压(Vblock),神经元就不能发放。通过将发放阈值Vthresh增加WRR(Vblock-Vthresh)来模拟动作电位后的相对不应期,其中WRR是无单位的权重参数。然后Vthresh以时间常数RR指数衰减到其基准值。
Synaptic mechanisms
除了固有的膜电压状态变量外,每个细胞还有四个额外的电压状态变量Vsyn,对应于突触输入。它们代表AMPA (AM2)、NMDA (NM2)和体细胞和树突GABAA (GA和GA2)突触。在输入事件发生时,突触权重通过Vsyn的逐步变化进行更新,然后将其添加到细胞的整体膜电压Vm。为了允许对Vm的依赖,突触输入通过dV=Wsyn(1-Vm/Esyn)改变Vsyn,其中Wsyn是突触权重,Esyn是相对于Vrest的反转电位。以下值用于反转电位Esyn:AMPA, 0 mV; NMDA, 300 ms; GABAA, –80 mV。在突触输入事件之后,突触电压Vsyn以时间常数syn呈指数衰减至0。syn使用以下值:AMPA, 20 ms; NMDA, 300 ms; 体细胞GABAA, 10 ms; 和树突状GABAA, 20 ms。树突突触(AMPA、NMDA、树突GABAA)输入之间的延迟及其对体细胞电压的影响选自3-12毫秒的均匀分布,而体细胞突触(体细胞GABAA)的延迟选自均匀分布(范围为1.8-2.2 ms)。除了那些参与学习的群体外,突触权重在一组给定的群体之间是固定的(参见表2中的可塑性"on")。
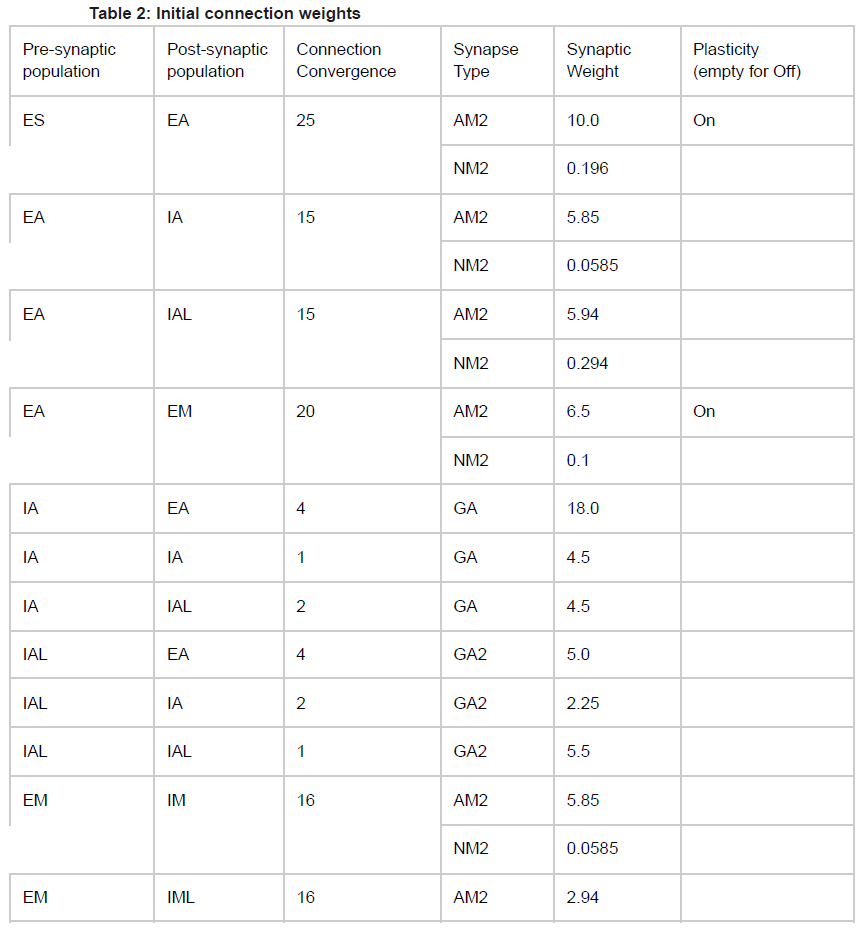
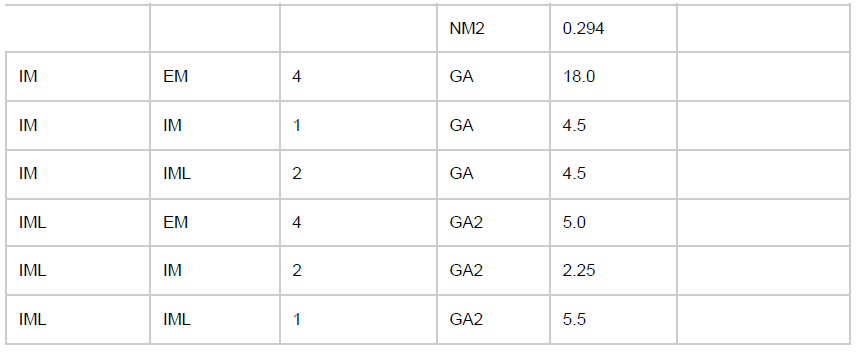
The Neuronal Weights
最初,调整了群体之间的权重,以允许在SNN模型的不同层/区域之间可靠地传输脉冲活动。然后,我们对两种训练策略使用相同的初始化。初始连接权重不受超参数调整的影响。
Training strategies
传统上,当SNN模型被训练来执行某种行为时,会使用受生物学启发的学习机制,例如STDP和RL (Anwar et al., 未注明日期)。这些机制在编码感觉环境的神经元和产生动作或动作序列的神经元之间建立关联,从而为特定的感觉线索产生适当的动作。感觉运动关联通常是通过感觉和运动神经元或其他相关区域之间突触权重的变化来实现的。因此,任何允许我们在改变神经元之间突触权重的同时评估SNN性能的方法都可以用于行为训练。在这里,除了强化学习策略:STDP-RL,我们还使用了进化策略方法(Salimans et al., 2017),我们在本文中将其表示为EVOL,以优化SNN模型中的突触权重以玩CartPole。
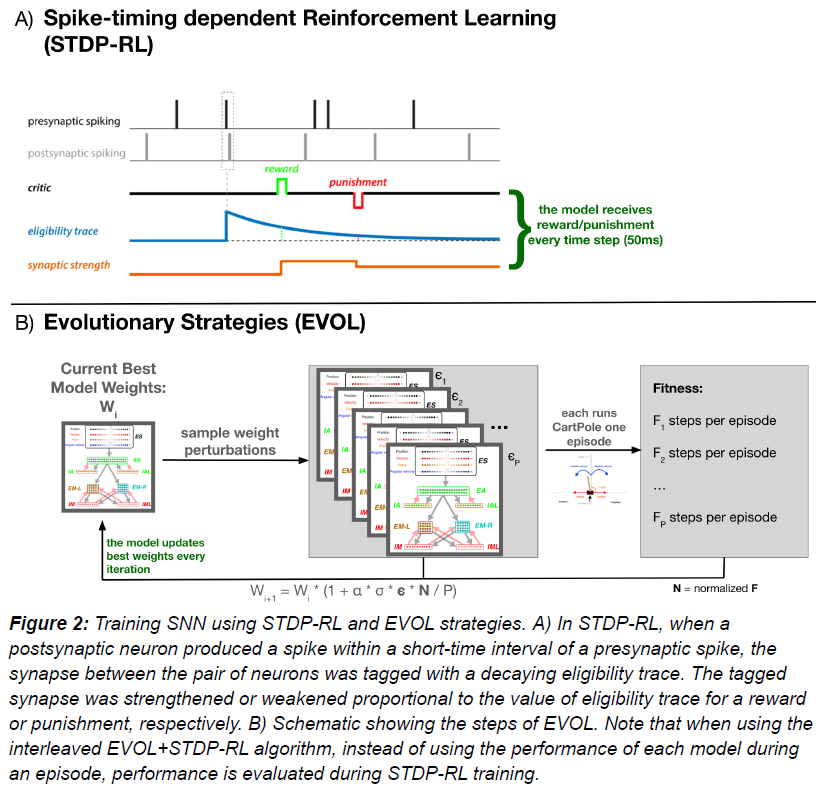
Spike-timing dependent Reinforcement Learning (STDP-RL)
我们在这项工作中使用了现有的STDP-RL机制(图2A),该机制是基于Izhikevich (Izhikevich, 2007)提出的远端奖励学习范式开发的,在脉冲神经网络模型中使用了变体(Neymotin et al., 2013; Chadderdon et al., 2012; Salvador Dura-Bernal et al., 2016; Chadderdon and Sporns, 2006)。我们的STDP-RL版本使用了一种脉冲时序依赖可塑性机制以及奖励或惩罚信号来增强或抑制目标突触。包括指数衰减的资格迹,以将时间远端信度分配给相关的突触连接。当突触后脉冲发生在突触前脉冲的几毫秒内时,这对神经元之间的突触连接符合STDP-RL的条件,并被标记为呈指数衰减的资格迹。后来,当在资格迹衰减到零之前给予奖励或惩罚时,标记的突触连接的权重会增加或减少,具体取决"critic"的值和符号,即增加(奖励)或减少(惩罚)。此外,突触强度的变化与critic交付时的资格迹值成正比。
传统上,当使用STDP-RL进行学习行为时,神经元网络模型中的所有可塑性突触连接都被平等对待(non-targeted STDP-RL)。该策略认为,突触前和突触后神经元之间的潜在因果关系以及相关的强化只会自动改变相关的突触连接。在传统的STDP-RL方法之上,我们使用了两个最近开发的有针对性的强化版本,通过有选择地向运动群体(EM)的不同子群提供奖励和惩罚(Anwar et al., 日期不详)。在第一个变体(targeted RL main)中,我们仅向产生动作的神经元子群(EM-LEFT或EM-RIGHT)提供奖励或惩罚。在第二个变体中(targeted RL both),我们还向相反作用的神经元子群提供了相反且减弱的强化。两种有针对性的方法都确保学习特定于生成动作的电路部分。此外,我们探索了向神经元群体提供(减弱的)"critic"值,这些值与直接产生运动动作的神经元群体(EA群体)相距仅一个突触。我们使用并评估了所有六种STDP-RL机制(三个targeted RL 版本 X 两个nonMotor RL版本)在超参数搜索期间的学习性能(详情见下文)。
Critic
对于STDP-RL,该模型依赖critic为模型的动作提供必要的反馈(图2A)。对于CartPole,我们选择了一位critic,该critic对使垂直杆更接近平衡位置的运动做出积极响应。我们计算了每个位置的损失,由角度和角速度输入状态的绝对值决定。critic的返回值将是前一个状态的损失和当前状态的损失之间的差值。如果以下状态之间的损失因智能体的移动而增加,则critic将返回负值,对应于惩罚。类似地,损失的减少将返回一个正critic值,对应于奖励。如果由于两个子群中的相同脉冲活动,智能体无法决定运动动作,则返回一个恒定的负惩罚。此外,由于在训练开始时critic受到惩罚的支配,为了避免权重降至零,模型需要相关的正奖励提升(ηpositivity)。critic最终被限制在最小值和最大值之间来在区间[-max_reward, max_reward]内保持奖励。


critic被实现为突触可塑性的粗略强化剂,与STDP事件一起工作。正如我们在超参数搜索(如下所述)中发现的那样,critic的大多数超参数对模型的最终性能几乎没有影响,我们相信许多不同的critic函数都适合我们的分析。更重要的是,对于突触权重归一化,临界值通过输出增益和稳态增益控制进一步调节,如下所述。
Hyperparameter Search
Evolutionary Strategies (EVOL)
EVOL算法已被证明是在强化学习控制问题中训练ANN的有效无梯度方法(Salimans et al., 2017)。在此,我们将这种学习技术应用于SNN,通过程序性地调整SNN的可塑性权重来解决CartPole问题。应该注意的是,在EVOL的ANN实现中,允许权重在值上不受限制,因此使用了附加权重。由于SNN没有负权重,我们改为使用乘法噪声,即我们以随机选择的百分比增加或减少权重。通过这种方式,我们能够将SNN权重限制为有效的正值,同时仍然有效地搜索所有可能的参数化。
正式地,我们的EVOL算法(图2B)包括以下步骤来改变每个突触的权重,对整个模型并行执行:(1) 在迭代 i 时,跟踪当前最佳突触权重:wi;(2) 从正态分布中采样权重扰动ϵ1..P的群体(P);(3) 对于每个权重扰动(ϵj),在CartPole环境中评估整个网络权重(wi * (1 + σ * ϵj))一回合;(4) 测量适应度(Fj)作为该回合的步数;(5) 通过减去群体平均适应度并除以群体平均标准差来归一化群体适应度值(Nj);(6) 基于归一化的适应度调节权重扰动并推导出新的最佳突触权重:
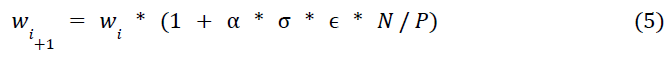
其中 α 是学习率,σ 是噪声方差,ϵ 和 N 分别是每个突触和归一化适应度的权重扰动的向量表征。我们只更新经历突触可塑性的权重(表2)。权重初始化(w0)与我们用于STDP-RL模型的初始权重相同。在这种情况下,STDP完全停用,EVOL训练程序每次迭代都会更新突触权重。
我们对EVOL模型进行了1500次迭代和P=10的总体训练,突触权重扰动的方差σ=0.1。我们使用了α=1.0的学习率。
Interleaved EVOL with STDP-RL
我们的交错EVOL/STDP-RL算法与上面应用的EVOL算法相同,只是做了一个修改:我们没有使用步骤(4)中的适应度,而是对每个群体成员进行额外的STDP-RL训练来模拟个体学习。之后,重新评估这些模型的适应度并用于更新下一次迭代的最佳权重。请注意,我们没有使用post-STDP-RL学到的权重,因为一生中的突触学习通常不会转移到后代。相反,pre-STDP-RL的权重与post-STDP-RL的适应度一起使用以产生次佳权重。我们注意到,对于这个算法,由于计算量很大,我们使用5作为群体大小,这可能解释了与基准EVOL算法的一些差异。然而,当使用10作为群体大小用于这种交错算法时,性能在性质上相似并且改进得更快(结果未显示)。
Synaptic weight normalization
Software
Evaluations
t-distributed Stochastic Neighbor Embeddings
Results
Training the SNN model to play CartPole
Comparing the performance of models trained using STDP-RL, EVOL, and EVOL+STDP-RL strategies
Comparing the learned SNN circuit dynamics.
Comparing the emergent Input-Output mappings after training with STDP-RL, EVOL, and EVOL+STDP-RL strategies.
Discussion
Comparison to artificial neural networks
Contribution to the field statement