郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!

Frontiers in computational neuroscience, (2021): 543872-22
Abstract
强化学习是一种范式,可以解释生物体如何学会在具有稀疏奖励的复杂环境中适应其行为。为了将环境划分为离散状态,脉冲神经元网络的实现通常依赖于涉及位置细胞或研究人员特别指定的感受野的输入架构。这是一个关于有机体如何在未知环境中学习适当行为序列的模型,这是有问题的,因为它无法解释所需表示的无监督和自组织性质。此外,这种方法的前提是研究人员知道如何对环境进行划分和表示,并根据环境的大小或复杂性进行不好的缩放。为了解决这些问题并深入了解大脑如何生成自己的任务相关映射,我们提出了一种学习架构,该架构将输入投影的无监督学习与表示层内的生物驱动集群连接相结合。这种组合允许将输入特征映射到集群;因此,网络自组织以产生清晰可辨的活动模式,可作为对输出预测进行强化学习的基础。在MNIST和Mountain Car任务的基础上,我们表明我们提出的模型比可比较的非聚类网络或具有静态输入投影的聚类网络表现更好。我们得出结论,无监督学习和集群连接的组合提供了适合进一步计算的通用表示基础。
Keywords: unsupervised learning, reinforcement learning, spiking neural network, neural plasticity, clustered connectivity
1. INTRODUCTION
神经系统从过去的经验中学习,根据处理要求逐渐调整其属性。无论是在纯粹的感官驱动情况下还是在高级决策过程中,学习的一个关键组成部分是开发足够且可用的内部表征,使系统能够评估、表示和使用环境的当前状态以采取动作以优化预期的未来结果(Sutton and Barto, 2018)。
虽然这些原理已在机器学习领域得到广泛利用,从而产生了高度熟练的信息处理系统,但与生物物理现实的相似之处往往只是概念上的。人工神经网络学习的标准方法是使用误差反向传播的端到端监督训练(LeCun et al., 2015; Kriegeskorte and Golan, 2019)。然而,尽管这些算法很熟练,但它们在生物约束下的合理性却非常值得怀疑(Nikolic, 2017; Marcus, 2018, 但参见例如Marblestone et al., 2016; Lillicrap and Santoro, 2019; Richards et al., 2019的反驳)。尽管越来越多的文献专注于通过调整误差反向传播来弥合这一鸿沟,使其在生物物理上更加兼容(例如,Sacramento et al., 2018; Bellec et al., 2019; Whittington and Bogacz, 2019),但这些方法与真正的神经元和突触动力学之间仍然存在脱节。
生物神经网络以离散脉冲(脉冲)运行,无需明确监督即可学习。突触功效根据局部信息(即突触前和突触后神经元的活动)以及非特异性神经调节门控因子(Porr and Wörgötter, 2007; Frémaux and Gerstner, 2016)根据任务需求进行调整。因此,任何获取内部表示的模型都应该符合这些(最小)标准,逐渐塑造系统的属性,以允许系统在不同任务约束下运行的方式学习状态空间的适当划分。此外,这些学习过程应该确保通用性,允许相同的电路被重用并在不同的输入流上运行,从中提取相关信息并根据处理需求以自组织的方式获取相关的动态组织。
建模研究采用了多种策略来允许系统在内部表征相关的输入特征(在强化学习的上下文中也称为环境状态)。例如,这可以通过手动选择神经元感受野(Potjans et al., 2009, 2011; Jitsev et al., 2012; Frémaux et al., 2013; Friedrich et al., 2014)来完成。指定的环境划分或通过均匀分布感受野,以覆盖整个输入空间(Frémaux et al., 2013; Jordan et al., 2017)。这些示例解决方案具有主要的概念缺陷。根据定义,手动划分环境状态空间是每个任务的临时解决方案;而均匀覆盖整个输入是一种更通用的解决方案,它只能在相对低维的输入空间中实现。在这两种情况下,研究人员都对给定任务的适当划分分辨率强加了假设,从而也隐含地影响了神经智能体的学习性能。因此,这两种方法都是不灵活的,并且它们的适用性受到限制。
假设捕获相关环境特征的足够内部状态的发展来自输入投射到电路的方式,这似乎很简洁。在储层计算范式中,输入投影充当非线性时间扩展(Schrauwen et al., 2007; Lukoševicius and Jaeger, 2009)。因此,相对低维的输入流被非线性地投影到电路的高维表示空间上。通过这种扩展性转换,神经基质可以开发合适的动态表征(Duarte and Morrison, 2014; Duarte et al., 2018)并解决非线性问题,使得在输入空间中不是线性可分的类可以在系统的表征空间。该属性依赖于神经基质的特性,作为非线性算子,以及随后的输入驱动动力学(Maass et al., 2002)。
储层计算模型的输出通常是一个简单的(通常是线性的)监督读出机制,对电路的动力学进行训练以找到预先确定的输入输出映射。自然,这种受监督的读数并不旨在构成生物学习的现实模型(Schrauwen et al., 2007),而是构成评估系统处理能力的指标。在生物系统中,人们会期望储层的输出预测适应局部信息,例如突触前和突触后活动,可能包含全局、扩散的神经调节信号。这里的一个复杂问题是,在很大程度上取决于一对神经元的脉冲活动的突触学习不可避免地容易受到该活动的随机性质的影响。
在这份手稿中,我们以生物学上合理的方式解决了上述划分输入空间和学习输出投影的问题。我们引入了一类新的脉冲神经网络模型,由一个输入层、一个基于脉冲神经元平衡随机网络的表示层和一个输出层组成。与经典的储层计算模型(Jaeger, 2001; Maass et al., 2002, 2003)相比,输入预测服从无监督学习(Tetzlaff et al., 2013),输出预测服从多巴胺调节强化学习规则而不是监督学习。此外,我们在表示层内的循环连接中引入了结构,以集群突触连接的形式(Rost et al., 2018; Rostami et al., 2020),这是一个受生物学良好启发的电路基序(Song et al., 2005; Perin et al., 2011)。我们证明,此功能与输入投影的无监督学习相结合,大大提高了网络的计算性能。集群以自组织的方式专门用于输入空间的特征,从而允许出现支持线性分离的输入的稳定表示。集群网络的低维动态(Litwin-Kumar and Doiron, 2014)为输出投影实现的三因素可塑性规则提供了稳定的基础,以使用强化学习策略学习适当的输入-输出映射。
我们首先使用XOR任务展示了无监督学习规则解决输入非线性的能力,允许表示层生成线性可分活动。然后,我们研究了完整模型在3位MNIST任务上的性能。我们表明,输入投影中的无监督学习允许输出投影以高精度学习正确的分类,即使学习是由强化信号(正确/不正确)而不是监督信号(正确类别的识别,更常用于分类任务)驱动的。表示层中集群的存在使网络比相应的非集群网络收敛速度更快,性能更高。具有可塑性输入投影的集群网络解决了非线性问题,捕捉了类内和类间的方差,并优雅地处理了这项具有挑战性的任务的高度重叠的输入。
最后,我们在具有稀疏奖励的连续空间和时间中定义的任务的闭环场景中测试模型:OpenAI Gym提供的山地车问题(Brockman et al., 2016)。再一次,具有可塑性输入投影的集群网络比非集群网络或具有静态输入投影的网络更有效地学习任务。
值得注意的是,对于这两个完全不同的任务,网络模型的配置几乎相同,仅在生成强化学习信号的机制上有所不同。特别是,集群的数量没有针对任务进行优化,并且输入到表示层的初始映射是随机的。因此,我们得出结论,我们的网络模型的三个组成部分,即输入投影的无监督学习、表示层的聚类连接和输出投影的强化学习,结合起来创建了一个拥有大量通用学习能力的系统,不需要以前的关于如何划分输入空间的知识,也没有使用生物学上不切实际的监督方法进行训练。我们预计无监督学习和集群连接的组件也可以用来放大其他学习网络模型的性能。
2. METHODS
2.1. Network Architecture
网络模型由三层组成,如图1A所示。可以在补充材料中找到网络及其参数的完整表格规范。
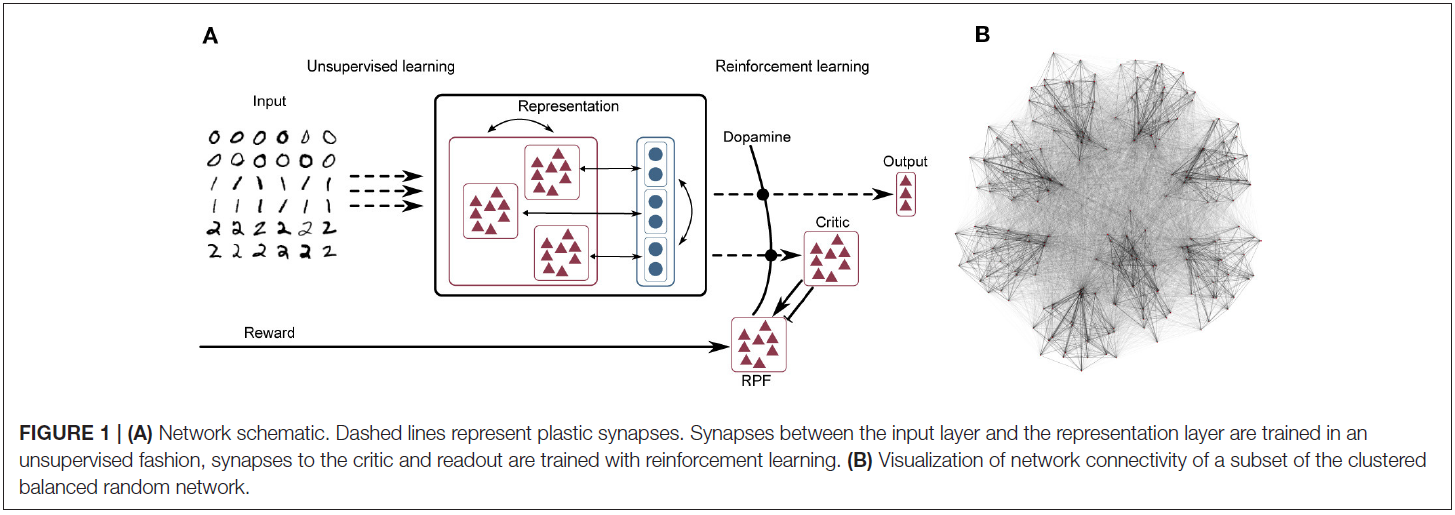
Input Layer
输入层是一群发放率调节的泊松脉冲神经元,最大发放率为Fmax。它将模拟输入数据转换为表示层的脉冲序列。例如,通过用图像中特定像素的强度gi刺激每个输入神经元,可以将灰度图像呈现给网络,从而产生发放率fi = Fmax · gi / 255的泊松脉冲序列。有关每个任务的输入转换的详细信息,请参阅第2.3节。
Representation Layer
输入层投影到表示层,由5000个IF神经元组成,其中4000个是兴奋性的,1000个是抑制性的。除了膜时间常数τm和施加的偏差电流Ibias外,神经元类型的参数化基本相同;有关参数的完整列表,请参阅补充材料。表示层的结构是一个平衡的随机聚类网络,如Rost et al. (2018)和Rostami et al. (2020)所述:连接概率是均匀的,但是一个簇内的突触权重(包含兴奋性和抑制性神经元)被放大,而簇之间的权重被缩小,这样总的突触强度保持不变(参见图1B网络可视化)。膜动力学遵循以下等式:

输入电流 I 由来自输入层和循环连接的突触输入以及恒定的偏差电流组成,对于相同类型的所有神经元(兴奋性/抑制性)都相同:

其中Ninp是输入神经元的数量,Nrep是表示层中的神经元数量。每个到达突触的脉冲都会引起一个指数形状的突触后电流,因此由一个突触前输入 i 的活动引起的输入电流由下式给出:

其中τs是指数突触后电流的放松时间,![]() 是神经元 i 的脉冲时间集,wi是连接突触的强度,δ是Dirac delta函数。
是神经元 i 的脉冲时间集,wi是连接突触的强度,δ是Dirac delta函数。
Output Layer
输出层由IF神经元组成,它们遵循与等式(1)中相同的动态。输出神经元形成一个带有横向抑制的赢家通吃电路。

其中Nout是输出神经元的数量,Ibg是来自泊松脉冲过程的背景输入,单个突触的当前动态由等式(3)给出。 类似于表示层的神经元,前馈连接是可塑性的,其动力学如下所述,而循环抑制连接和来自泊松源的连接是静态的。输出神经元的数量对应于数据集中标签的数量(对于分类任务)或动作的数量(对于具有离散动作的强化学习任务)。由于强横向抑制,在任何给定的时间点,只有一个输出神经元是强烈活跃的,即具有最高加权输入的神经元。
为了确定要选择哪个标签(或动作),输出层神经元的脉冲用指数核进行低通滤波;然后将预测的标签(或选择的动作)定义为与具有最高活动的输出神经元相关联的标签(或动作)。
Actor-Critic Circuit
Actor-Critic方法通常用于无法立即获得强化信号的强化学习任务(Sutton and Barto, 2018)。在这个框架中,actor选择动作,而critic计算环境状态的期望值V(S) (即折扣后的总期望未来奖励)。从动作前的状态价值与动作获得的奖励和新状态的折扣价值之和之间的差值,可以推导出奖励预测误差(RPE) δt,它表示选择的动作是否产生比预期更好或更差的结果:
![]()
其中γ是折扣因子。对于接近于零的γ值,智能体是短视的,并且更喜欢即时奖励而不是未来的奖励。接近1的值对应于未来奖励的强权重。然后使用这个RPE来更新前一个状态的期望价值和智能体的策略,使得导致比预期更好状态的动作变得更有可能,反之亦然。在神经活动的背景下,Frémaux et al. (2013)表明,与多巴胺浓度相关的连续信号可以起到奖励预测误差的作用:
其中 v 是critic神经元(或神经元群体)的发放率,r 是直接从环境中收到的奖励,τr是折扣时间常数。
我们将critic实现为20个泊松脉冲神经元的群体。这个群体的发放率由当前活跃的群体以及将集群的神经元连接到critic神经元的突触的权重决定。为了建立等式(6)的必要关系,我们将critic群体的较高发放率 ν 解释为较高的值V(S),在等式(5)的意义上,对于与活动集群相关的状态(或簇)。critic神经元投射到代表RPE的1000个泊松脉冲神经元,这反过来产生如上所述的多巴胺能浓度D(t)。实现了v(t)的瞬时变化(如Jordan et al., 2017)作为从critic到RPE的双重连接,其中一个连接是兴奋性的,具有1毫秒的小延迟,第二个连接是抑制性的,延迟较大,为20毫秒(Potjans et al., 2009; Jitsev et al., 2012)。请注意,并未对该电路的生物学合理性做出任何声明;它只是一个最小的电路模型,可以生成足够的奖励预测误差,从而能够研究聚类结构在为强化学习任务生成有用表示中的作用。RPE信号作为第三个因素进入表示层和输出层(即actor)之间突触的可塑性,如下一节所述。
2.2. Plasticity
2.3. Tasks
2.3.1. Logical Operations Task
2.3.2. MNIST Task
2.3.3. Mountain Car Task
2.4. Simulation Tools
3. RESULTS
3.1. Learning Input Representations and Resolving Non-linearities
3.2. Feature Extraction in a Classification Task
3.2.1. Self-Organization of Feature Extracting Representations
3.3. Continuous Time and Space and Delayed and Sparse Reward
4. DISCUSSION