郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！
The Journal of neuroscience: the official journal of the Society for Neuroscience, no. 40 (2010): 13326-13337
Abstract
最近的实验表明，神经刺激调节了脉冲时序依赖可塑性。我们推导了大量关于奖励相关行为的学习规则类别成功学习的理论条件，其中，赫布突触可塑性以标志奖励的全局调节因子为条件。我们证明了该类别中的所有学习规则都可以分为捕获神经元发放和奖励的协方差的项和代表无监督学习的影响的第二项。如果神经调节信号编码了奖励和期望奖励之差，则可以抑制通常对基于奖励的学习有害的无监督项，但前提是要分别为每个任务和刺激计算期望奖励。如果要同时学习多个任务，则神经系统需要一个内部critic，该critic能够预测任意刺激的期望奖励。我们表明，与critic一样，奖励调节脉冲时序依赖可塑性能够以数十毫秒的时间分辨率学习运动轨迹。与TD学习的关系，基于块的学习范式的相关性以及与critic一起学习的局限性也得到了讨论。
Introduction
在行为学习范例中，动物改变其行为以便获得奖励(例如，果汁或食物颗粒)或避免反感刺激(例如，脚部震动)。尽管行为学习的心理现象学已得到很好的发展(Rescorla and Wagner, 1972; Mackintosh, 1975)，并且有许多奖励学习的算法方法(强化学习)(Sutton and Barto, 1998)，但行为学习与突触可塑性之间的关系尚不完全清楚。
突触的长期增强(LTP)或长期抑制(LTD)的经典实验和模型符合赫布学习的传统(Hebb, 1949)，并研究突触权重随突触前和突触后活动的变化。它以频率依赖性(Bliss and GardnerMedwin, 1973; Bienenstock et al., 1982)，电压依赖性(Artola et al., 1990)或脉冲时序依赖性(STDP)(Gerstner et al., 1996; Markram et al., 1997; Bi and Poo, 1998; Sjöström et al., 2008)的形式存在。从理论角度(Dayan and Abbott, 2001)，这些可塑性形式与无监督学习规则有关，即未考虑突触变化的行为相关性。然而，最近发现，包括STDP在内的许多可塑性实验的结果都取决于神经调节作用(Seol et al., 2007)，特别是多巴胺的存在(Jay, 2003; Pawlak and Kerr, 2008; Wickens, 2009; Zhang et al., 2009)，一种神经调节剂，已知可编码行为奖励信号(Schultz et al., 1997)。受这些发现的启发，许多理论研究对以下假设进行了假设：奖励调节STDP可能是奖励学习的神经基础(Seung, 2003; Xie and Seung, 2004; Farries and Fairhall, 2007; Florian, 2007; Izhikevich, 2007; Nordon, 2007; Legenstein et al., 2008)。
在此，我们要解决的问题是，奖励调节STDP引起的突触功效变化是否以及在何种条件下具有增加动物获得的奖励量的预期行为效果。为此，我们研究了种类繁多的奖励调节学习规则，并表明该类别中的大多数学习规则都可以解释为对奖励敏感的学习部分与无监督且独立于奖励的部分之间的竞争。我们表明，要为任意学习任务启用基于奖励的学习，无监督的组件必须尽可能小。如果缺少无监督的赫布学习或大脑中包含期望奖励的预测因子，则可以实现此目的。我们通过模拟两个不同的学习规则来说明我们的理论论点：R-max规则，该规则在理论上旨在增加学习过程中的奖励(Xie and Seung, 2004; Pfister et al., 2006; Baras and Meir, 2007; Florian, 2007)；以及R-STDP规则(一个简单的STDP规则，其幅度和符号由正或负奖励调节(Farries and Fairhall, 2007; Izhikevich, 2007; Legenstein et al., 2008))。我们在一组最少的任务上测试了学习规则。首先，一个脉冲序列学习toy问题；第二，更现实的轨迹学习任务。在这两项任务中，神经元必须以时间上精确的方式做出反应，以使脉冲时间变得重要。
Materials and Methods
Neuron model. 在模拟中，突触后神经元是具有指数逃逸率的简化脉冲响应模型(SRM0)神经元(Gerstner and Kistler, 2002)。SRM0是一个简单的点神经元模型，可以看作是LIF神经元的泛化。神经元的膜电位是突触前电位(PSP)的线性和，发放是随机的，发放概率随膜电位而增加。更正式地说，这些神经元的输出脉冲序列是不均匀的更新过程，具有瞬时发放率：
其中ρ0 = 60 Hz是阈值时的发放率，θ = 16 mV是阈值，Δu = 1 mV控制逃逸噪声的量，ui(t)是神经元 i 的膜电位(相对于静息电位测量)，定义为：
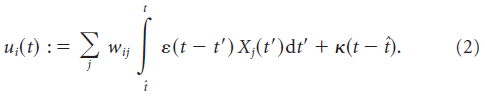
在此，ε(t)表示突触后电位的形状，wij是突触前神经元 j 和突触后神经元 i 之间的突触权重。
是第 j 个突触前神经元的脉冲序列，其建模为δ函数之和，
描述了时间
上最后一次脉冲之后的脉冲后电位。κ控制神经元的不应期程度。对于多个突触后脉冲，不应该累积不应性效应，因为我们不对多个突触后脉冲求和以得到κ。鉴于神经元的发放率约为5 Hz，无论如何累积效果都不会发挥重要作用。我们用：
对于s < 0，ε(s) = 0，并且：
其中ε0的PSP振幅为5 mV，膜时间常数τm = 20 ms，突触上升时间τs = 5 ms，复位电位ureset = -5 mV。在极限Δu→30中，该模型成为确定性IF神经元模型，并以θ为阈值。
对于SRM0神经元，固定的一组输入脉冲X在任何短时间间隔Δt中的脉冲期望数目由瞬时发放率ρ(t)确定：
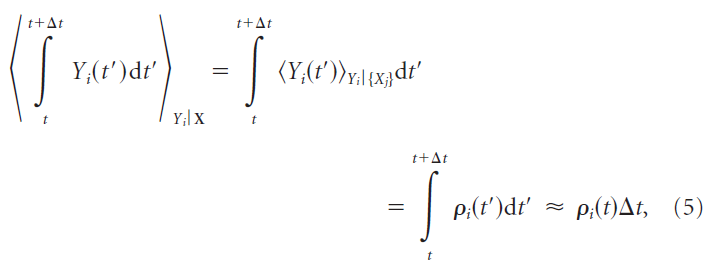
其中神经元的输出脉冲表示为
。因为这在任意短的时间间隔内保持不变，所以瞬时发放率等于瞬时脉冲频率
(对于固定刺激
)。请注意，ρi(t)也取决于突触前脉冲序列，因为它取决于膜电位
。
Learning rules. 我们研究了一类奖励调节的突触学习规则，其中无监督的赫布学习规则(UL)导致一组突触权重wij中的候选变化eij，仅在存在与时间相关的成功信号
时才有效，其中
是奖励R的单调函数：
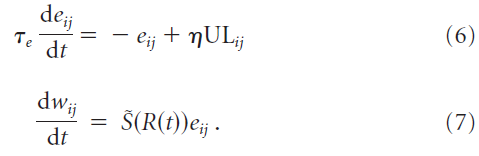
学习率η决定学习的速度。如果无监督项ULij消失，则候选权重将eij衰减为零，且时间常数为τe = 500 ms。候选权重变化eij被称为强化学习中的资格迹(Williams, 1992; Sutton and Barto, 1998)。在我们的模拟中，成功信号在试验结束的时间t = T给出。当
时，则每次试验的总权重变化为：
我们通过在每个试验开始时将资格迹重置为0，来模拟一个比τe大得多的试验间隔时间。
我们选择了资格迹的衰减时间常数，该常数为试验时间的一半：T = 2τe。这意味着从试验开始起的贡献ULij进入最终资格迹eij(T)，比从试验结束起的贡献少e-2 ≈ 0.14倍。然而，学习规则能够解决问题，并且对所学习的脉冲序列的目视检查(数据未显示)在试验结束时没有明显的偏差。资格迹τe的时间常数越长，学习越容易。
为了便于说明，我们模拟了两种等式6和7的类型的学习规则：R-STDP，STDP的经验性奖励调节版本(图1A)；和R-max，这是一种从理论上的奖励最大化原则衍生而来的学习规则。
The R-STDP learning rule. 对于R-STDP，资格迹的驱动项ULij是脉冲时序依赖可塑性模型(Gerstner and Kistler, 2002)：
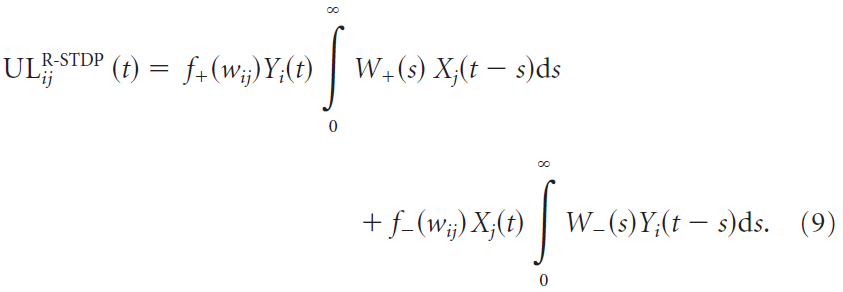
是pre-before-post时序的学习窗口(+，对于正的成功信号为LTP)和post-before-pre时序(-，对于正的成功信号为LTD)。
和
分别控制pre-before-post和post-before-pre部分的幅度与它们的时间尺度。默认值为A+ = 0.188，A- = -0.094，τ+ = 20 ms和τ- = 40 ms。通过这种参数选择，可以平衡pre-before-post和post-before-pre部分，即A+τ+ = -A-τ-。在模拟中，我们改变了两个部分之间的平衡，我们更改了post-before-pre窗口的幅度A-，并保持所有其他参数不变。LTD/LTP比λ定义为λ = A-τ-/A+τ+。因此，假设成功信号为正，则λ = -1表示LTP和LTD的平衡，而λ = 0表示在post-before-pre脉冲时序之后没有LTD。
函数
描述了pre-before-post和post-before-pre窗口的权重依赖性。在我们的模拟中，我们使用f+(w) = (1 - w)α和f-(w) = wα (Gütig et al., 2003)，并考虑α等于0或1。请注意，对于α = 0，该模型简化为所谓的加法STDP模型(Song et al., 2000)。除非另有明确说明，否则将使用边界为0 < w < 1的加性模型。请注意，我们在等式9中的项ULij中包括了权重依赖性，但是，它可以引入等式7。在我们的模拟中，学习足够缓慢，并且两种方法导致几乎相同的结果。
The R-max learning rule. R-max规则是明确地出于奖励最大化目的而派生的(Xie and Seung, 2004; Pfister et al., 2006; Florian, 2007)，并依赖于具有逃逸噪声的脉冲响应模型神经元。无监督学习规则UL由下式给出：
其中，Δu如等式1中定义。有关规则的正式推导，请参见Pfister et al. (2006)。Xie和Pfister (2004)的推导是相似的，只是它没有考虑神经元的不应期。
R-max规则对于无监督学习是无用的，因为无监督学习规则ULij的集合平均(以及资格迹的集合平均<eij>)消失了，与输入统计数据无关，即：
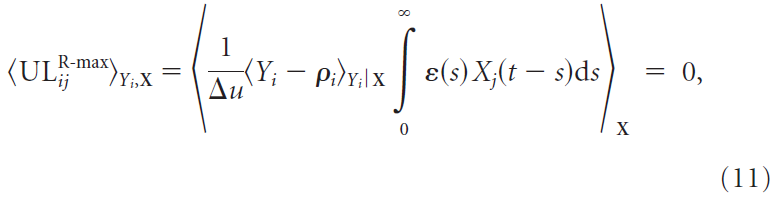
因为
。学习是通过突触后脉冲序列Yi(t)与奖励之间的相关性进行的。如果在时间 t 的脉冲与稍后某个时间 t' 的奖励正相关(即
，其中t' - t不大于资格迹的时间常量τe)，那些在时间 t 通过其PSP导致脉冲的突触被加强，从而增加了下次发生相同刺激时脉冲的可能性。
Comparing R-max with R-STDP. 假设试验以正的成功信号[S(R) > 0]结束。这两个规则对LTP的要求非常相似；加法R-STDP的pre-before-post部分(等式9中
，假设α = 0)和R-max的正部分(等式10中
)仅在重合核的详细形状W+(s)和ε(s)上有所不同。但是，LTD的要求却大不相同。在R-STDP中，LTD取决于突触后发放事件，而R-max仅考虑瞬时发放率ρi。
请注意，这两个规则都具有在全局神经调节信号控制下的局部赫布规则的结构。因此，原则上，这两个规则都是在大脑中进行行为学习的生物学合理的候选者(Vasilaki et al., 2009)。
Network. 该网络由五个相互不连接的SRM0神经元组成，它们接收50个公共输入脉冲序列(用于轨迹学习任务的200个神经元和350个输入)。所有输入突触都是可塑性的，并且遵循上述两个学习规则之一。对于加性STDP模型(α = 0)，通过将超出边界的权重重置为关联的边界值，将突触权重在算法上限制为间隔wij ∈ [0, 1]。对于乘法模型，我们使用f+(w) = (1 - w)α和f-(w) = wα(其中α = 1)。在学习开始之前，所有突触权重都初始化为0.5 (对于轨迹学习任务为0.15)。为了公平地比较学习规则，可以分别调整每个规则的学习率，以便获得该规则可获得的最大性能。对于脉冲时序学习任务，对于多模式学习，除η = 0.33以外η = 1，而η = 0.2更改LTD/LTP比λ。使用时间步长δt = 0.1 ms (对于轨迹学习任务为δt = 1 ms)来模拟网络。
Spike-timing learning task. 所有模拟都包含一系列的5000次试验(在学习多种模式的情况下更多；请参见下文)，每次试验持续1 s。在每次实验期间，都会向网络呈现一个输入脉冲模式。根据在随后的试验中输出神经元产生的脉冲序列Yi来计算神经元和特定于试验的得分，然后对输出神经元进行平均，以产生全局奖励信号Rn(图1B)。这里有两点需要注意：尽管在每次试验中输入的脉冲模式可能是相同的，但由于输出的神经元是随机的，因此输出的模式将有所不同。而且，尽管脉冲模式学习似乎是一项监督学习任务，但特定的设置却将其转变为强化学习问题，因为网络中的所有神经元在试验结束时都会收到单个标量奖励信号，而不是每个时间点每个神经元的详细反馈信号。因此，他们必须解决所谓的信度分配问题：哪个神经元在正确的时间发放脉冲并导致全局成功S(Rn)？
仅在每次试验结束时，成功信号S(Rn)才会传递到网络，从而触发突触可塑性。我们使用与奖励线性相关的成功信号：
。
是奖励的运行试验均值：
，带有τR = 5(多模式方案除外，请参见下文)。C是控制平均成功信号的参数，因为成功的运行试验均值为
。如果没有另外说明，则为C = 0，这导致
。注意，对于C = 0，成功信号可以解释为奖励预测误差，因为它计算了期望奖励的内部估计与实际奖励之差。
Learning a single target output pattern. 在此，输入由一组固定的脉冲序列Xj组成，持续时间为1 s，这些脉冲序列由均质泊松过程以6 Hz的频率生成。通过将输入模式呈现给网络以一组参考突触权重来生成目标输出模式
，参考突触权重是从间隔[0, 1]上的均匀分布中分别得出的。此过程可确保目标模式是可学习的。但是请注意，神经元是随机的，因此可能存在一组突触权重，该权重比目标权重具有更高的可靠性来重现目标模式。
Reward scheme. 根据Victor和Purpura (1997)引入的脉冲编辑度量Dspike[q]，通过比较突触后脉冲序列Yi和参考脉冲序列(图1B)，计算神经元特异性得分
。从脉冲序列添加或删除脉冲的成本为1单位，脉冲移位Δ的成本为Δ/q，其中q = 20 ms是固定参数。差异度量Dspike(X, Y)是将脉冲序列X转换为Y的最小可能成本。我们使用该度量的规范化版本
。在此，Ni和
分别是第 i 个输出脉冲序列和对应的目标脉冲序列的脉冲计数。在此定义下，
取0到1之间的值，其中
表示输出和目标脉冲序列之间的完美匹配。例如，假设目标脉冲序列具有30个脉冲。在这种情况下，值0.8对应于具有相同数量脉冲的突触后脉冲序列，但每个距离最近的目标脉冲都相距8 ms，或者与只有20个脉冲的突触后脉冲序列相对应，但全部完美的时序。图1C显示了脉冲序列得分的示例。仅比较输出和目标脉冲序列的脉冲计数的另一脉冲度量是
。
Multipattern learning. 为了测试是否可以学习多个模式，我们以与上述单模式场景相同的方式生成了Npattern个输入和目标输出脉冲模式，并对所有模式使用了相同的参考权重。在每个试验期间，随机选择一种输入模式，然后将输出与相应的目标进行比较。所有模式出现的可能性均等。这些模拟中的试验次数为每个模式5000次；这样可以确保每个模式的平均展示次数与单模式场景下相同。
如在单模式场景中一样，计算神经元特定得分
，但是从奖励中减去以产生成功信号的奖励基准
是通过两种不同的方法来计算的，或者通过上述简单的试验均值，但使用时间常数τR → τR x Npattern来说明每种模式减少的发生，或通过为每种输入模式μ计算单独的试验均值
来解决：
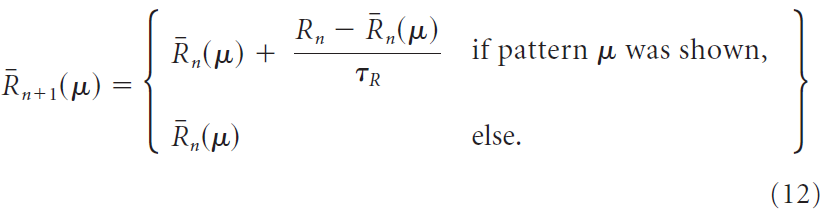
后者规定了刺激特定的奖励预测系统，也称为critic。
作为刺激特定奖励预测的替代方法，我们实施了分块学习方案。在500个试验的块内，仅提出了一种刺激措施。这些块按A, B, A, ... 的顺序交替排列。在块之间，通过将平均奖励
重置为下一个块中第一个试验的奖励值，我们模拟了一个块间中断，该间隔长于奖励基准估计的时间常数τR。
Trajectory learning. 最后，我们以更现实的学习范例说明了我们的发现。设置与上面的脉冲时序学习任务相同，不同之处在于输入是随机的，网络较大，输出的神经元被编码为运动，并根据整个群体产生的轨迹与目标轨迹之间的相似性得到奖励。
输入的神经元是异质不应期泊松过程。有350个输入神经元，其发放率ρj(t)是高斯(函数)的总和，其中心
是随机分配的，即：
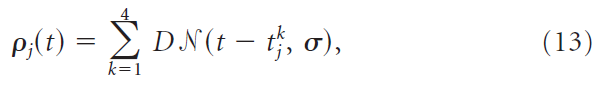
其中N表示归一化的高斯函数。SD为σ = 20 ms，因子D = 1.2控制每个高斯(函数)的平均脉冲数。一次选择发放率的时间过程ρj(t)(见下文)，然后在整个学习过程中固定下来；在两次试验之间，只有脉冲实现发生了变化。更精确地，对于每个输入神经元，等式13中的中心
是从包含一组集合{0, 20, 40，... , 980 ms}的许多重复项的中心池中随机抽取的，但不进行替换，以填充所有输入神经元。将350个输入神经元分为三组：针对所有模式发放50个非特异性神经元，仅在呈现各自模式的情况下才发放两组150个针对模式的神经元。泊松过程具有指数不应期，频率τrefr = 20 ms。给定最后一个脉冲
，在 t 和Δt之间出现脉冲的概率为
，其中
是神经元 j 发出的最后一个脉冲的时间。
突触后神经元活动的解码是根据群体矢量编码方案完成的(Georgopoulos et al., 1988)。通过将输出脉冲序列Yi(t)与因果核ζ(s)卷积来获得输出频率ri，即
。 在我们的解码方案中，15 ms的时间分辨率类似于神经修复术中常用的分辨率(Schwartz, 2004)。200个输出神经元中的每一个都对应于首选方向矢量，该方向矢量 i 是从单位球面上的均匀分布绘制的。输出运动由归一化的时间依赖群体矢量给定：
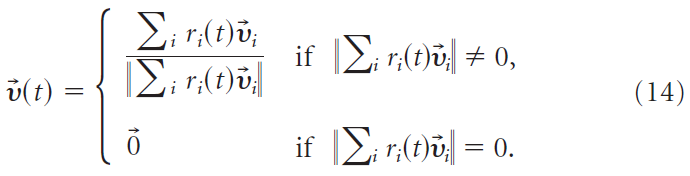
代表运动的瞬时方向。输出轨迹
通过积分
获得。为了避免这两个任务的强烈干扰，目标轨迹被选择为位于正交平面。通过将目标运动
和实际运动
的标量乘积的正部分来计算奖励(在整个试验取均值)，即
。
连同网络的大小一起，更改了许多参数的值，以使突触后频率保持与脉冲序列学习任务中相同的数量级。EPSP振幅降低到ε0 = 4mV，并且突触权重被统一初始化为wij = 0.15。R-STDP的学习率是η = 0.15，R-max的学习率是η = 0.0625。这些值在初步运行中产生了最高的性能。
Performance measure. 通过对模拟的最后100次尝试中的奖励Rn进行平均，来评估网络的性能。为了获得性能的统计量度，所有模拟都以不同的输入/目标模式运行了20次。
在显示性能的图中，我们还给出了具有初始(均匀)权重的网络所获得的平均奖励。这对应于学习之前网络的性能。如果网络在学习后的性能比该级别差，则它实际上是未学习的。对于脉冲序列学习任务，我们还显示了参考权重(用于生成目标脉冲序列的权重)的平均性能，该平均权重的计算方法如下：从参考权重生成100个输出模式，其中与学习任务中的输入相同。参考权重性能是这些模式的成对得分的均值。由于神经元是随机的，因此带有正确(即参考)权重的神经元将不会始终生成目标脉冲序列，而是会分配可能的输出脉冲序列。因此，参考性能小于1。如果神经元必须学习少量的目标脉冲序列，则它们可以以参考权重胜过网络，因为它们可以专注于目标模式。但是，随着目标模式数量的增加，专业化的自由度以及因此的性能都会下降。在许多目标模式的限制中，参考权重是可能的最优权重集，因此参考性能成为网络性能的上限。
The role of the reward prediction for the R-max rule. 使用R-max规则进行的仿真显示，即使无偏的规则不需要奖励预测系统起作用，也可以从其存在中获利。critic对无偏规则的这种有益作用的原因在于带噪论证。让我们假设学习过程已经收敛，即权重变化平均为零。请注意，这并不意味着在任何给定的试验中权重变化都为零，而是由于神经元的随机性，其在零附近波动。这些波动继而导致突触权重围绕平衡波动，该平衡(理想情况下)对应于产生最高奖励的那些权重。权重变化的试验间变化的减小允许权重保持更接近于此(可能是局部的)最优值，因此产生更高的平均性能。如下面所示，可以通过降低学习率(当然也可以降低学习速度)或使用奖励预测系统来降低权重变化的从试验到试验的变异性。
在成功信号S(R) = R - b为奖励减去任意奖励基准 b 的假设下，让我们考虑权重变化在其均值附近的方差。奖励更新规则(公式8)求平方可以得出：
可以通过设置相对于b = 0的var(wij)的导数并求解最优基准来计算该方差最小的基准 b 的值(Greensmith et al., 2004)：
该公式表明，尽管平均奖励R可能不是最优的，但它可以用作最优基准的近似值，其精度取决于奖励与资格迹的平方的相关性。在我们的模拟中，奖励取决于多个输出神经元，因此奖励与任何单个神经元的资格迹平方的相关性可能很小。因此，critic预测的平均奖励接近最优奖励基准，以最小化权重变化的试验变异性。降低的变异性可产生更高的性能。这就是为什么在存在critic的情况下R-max规则的性能会提高的原因。
图1. 使用奖励调节的STDP学习脉冲序列响应。A，奖励调节STDP。取决于突触前和突触后脉冲的相对时间(蓝色，pre-before-post；红色，post-before-pre)，突触权重的候选变化eij会出现。它们会衰减，除非它们被成功信号S(R)永久地印在突触权重wij中。候选变化eij和成功信号S(R)的符号都会影响实际权重变化的符号(即，如果两者均为负，则权重变化为正)。B，学习任务。在每个试验中，相同的输入脉冲模式(左)都呈现给网络。将五个突触后神经元的输出脉冲序列(右，黑色)与五个目标脉冲序列(右，红色)进行比较，得出一组神经元特定得分
，将其在所有输出神经元上平均以产生全局奖励信号Rn。触发突触可塑性的成功信号S(Rn)是全局奖励Rn的函数。C，通过输出神经元之一学习目标脉冲序列。目标脉冲时间以浅红色显示，而输出神经元的实际脉冲时间由彩色脉冲序列指示。每行对应于学习的开始(品红色)，中间(绿色)和结束(黄色)的不同试验。神经元的个体得分
在右侧显示(值越高表示学习越好)。D，学习曲线。在学习回合(R-STDP；学习到一个单一输出模式)期间，奖励Rn的进化(灰色点，为清晰起见，仅显示25％)。垂直彩条与C中所示的试验匹配。黑色曲线显示平均分数Rn，该分数用于计算成功信号
，如底部所示。虚线表示学习之前的性能，虚线表示参考权重的性能(请参见"材料和方法")，表示性能良好。
Results
在典型的操作性条件调节实验中，口渴的动物如果响应刺激而执行所需的动作，则会获得果汁奖励。当动物了解刺激，动作和奖励之间的应变时，它会改变其行为，以使其最大化或至少增加其接收到果汁的量。为了将这种行为学习范式带到细胞水平，我们可以从概念上放大并专注于单个神经元。它的输入反映了刺激，其输出影响了动作的选择。在这张图中，学习与突触修改相对应，在重复相同的刺激后，神经元的输出就会发生变化，从而使收到奖励的动作变得更有可能。能够解决该学习任务的任何突触学习规则都必须取决于三个因素：突触前活动(刺激)，突触后活动(动作)以及奖励的某些生理关联。我们将这种学习规则称为基于奖励的学习规则，如果将神经元活动描述为脉冲(相对于平均发放率)，则将基于奖励的学习规则用于脉冲神经元或奖励调节STDP。
关于赫布学习的标准范例，包括传统的STDP实验和STDP模型，仅控制突触前和突触后活动。这些范式被称为无监督范式，因为它们没有考虑到神经调节剂的作用，这些神经调节剂会发出奖励存在或不存在的信息(Schultz et al., 1997)。我们发现，针对脉冲神经元的大量基于奖励的学习规则可以表述为由奖励调节的无监督学习规则(请参见"材料和方法")。在这些规则中，无监督的赫布规则ULij = prej x posti (其中prej和posti分别是突触前和突触后活动的函数)在突触中从突触前神经元 j 到突触后神经元 i 留下一些生物物理迹eij。除非全局奖励相关的成功信号S(R)将迹eij转换为与S(R) x eij成比例的永久权重变化Δwij，否则该迹将衰减回零。eij量(在强化学习中称为资格迹)可以看作是候选权重变化，而Δwij是实际权重变化(图1A)。总体而言，赫布资格迹与全局成功因素之间的相互作用是适用于脉冲神经元(Seol et al., 2007; Pawlak and Kerr, 2008; Zhang et al., 2009)的三因素规则的一个例子(Reynolds et al., 2001; Jay, 2003)。
Unsupervised learning maintains an unsupervised bias under reward modulation
我们想知道无监督规则UL的选择和成功信号的实现是否相互影响。让我们首先考虑以下情况：成功信号S(R)不受奖励调节，但取恒定值：S(R) = const。在这种情况下，所有候选权重变化eij都将印记在权重(Δwij ～ eij)中，奖励不再控制可塑性，并且有效地学习变得无监督。可以预期，如果通过奖励对成功信号进行弱调节，则这种情况将基本保持不变，只要调节比成功信号的均值小即可。为了将由奖励调节驱动的学习组件的成功信号的均值产生的无监督学习组件分开，我们将变化拆分为等式7中的权重，将多个试验的均值分为两个项：
其中
表示成功信号与候选权重变化eij之间的相关性。由于eij受依赖于突触前和突触后活动的赫布学习规则的驱动，因此它会将突触后神经元的输出反映到给定的输入，因此等式17中的第一项可以获取神经元行为与奖励之间的协方差。因此，这种对奖励敏感的学习成分可以潜在地检测奖励行为。
相反，行为和奖励的协方差与第二项无关，因为它仅取决于成功信号的均值<S(R)>。资格迹的均值<eij>反映了仅无监督学习规则ULij的平均行为，从而给权重动态带来了无监督偏差。平均成功信号，我们称为成功偏移
，作为权衡参数，确定学习的奖励敏感成分与无监督偏差之间的平衡。
图2. 与R-max不同，R-STDP对成功信号中的偏移
敏感。A，成功信号偏移对学习性能的影响。数以千计的试验(垂直轴)后获得的奖励显示为成功偏移C的函数，以学习前奖励的SD σR为单位给出。实心圆圈中，R-max(红色)对成功偏移具有鲁棒性，而R-STDP(蓝色)即使偏移很小，也会失败。R-STDP对于负偏移C的性能下降到学习之前的性能以下(虚线)。空圈，降低学习率(η = 1 → η = 0.06)并允许神经元学习更多试验(Ntrials = 5000 → Ntrials = 80000)补偿了R-max偏移的影响，但并未显着提高R-STDP的性能。均值是针对20种不同的模式集。误差线显示SD。B, C，非零成功偏移将R-STDP偏向无监督学习。对于R-STDP (B)和R-max (C)，显示了在输入模式和输出神经元上汇集的第一个输出脉冲的延迟与第一个目标脉冲的延迟。如果学习成功，则两个值都匹配(灰色对角线)。R-max (C)和无偏的R-STDP (B，蓝点)就是这种情况，但是具有非零成功偏移的R-STDP显示了无监督规则的行为：突触后神经元的发放时间早于C > 0的目标(B，绿点)和更高版本的C < 0 (B，红点)。D, E，R-STDP不能通过权重依赖性(D，α = 1，绿点；从A重绘的红色和蓝色点)或通过pre-before-post和post-before-pre窗口大小比例λ的变化来挽救(E)。F，结果并不特定于奖励计划。与A相同，但具有脉冲计数分数而不是脉冲时序分数。在A，D–F中，虚线表示学习之前的性能，而虚线表示参考权重的性能。
Unbiased learning rules are relatively robust to changes in success offset
学习规则中的无监督偏差无助于增加获得的奖励量，因为它对资格迹和奖励之间的相关性不敏感。如果目标是最大化奖励(即获得尽可能多的果汁)，则学习规则中无监督偏差的影响必须很小。根据等式17，这可以通过减小成功偏移
或平均资格迹<eij>来实现。从奖励最大化原则(Xie and Seung, 2004; Pfister et al., 2006; Florian, 2007)得出的学习规则(如R-max(请参见"材料和方法"))使用的是无偏资格迹(<eij> = 0)独立于输入统计信息。换句话说，基本的无监督学习规则UL是无偏的。因此，我们的理论预测R-max对成功偏移不敏感。
让我们假设最优动作对应于突触后神经元的一些目标脉冲序列(图1B)。如果实际输出接近目标脉冲序列，则给出奖励。奖励以全局神经调节反馈信号的形式传达，传递给所有神经元和所有突触，并且可以通过广泛分布的多巴胺能神经元的轴突靶向模式在大脑中实现(Arbuthnott and Wickens, 2007)。图2A显示，即使成功偏移明显不同于零，配备有无偏突触学习规则(R-max)的神经元也可以响应给定的输入脉冲模式成功学习目标脉冲序列。随着学习成功率的提高，性能的逐渐下降可以通过较小的学习率来抵消(图2A)，表明这是由于噪声问题引起的(Williams, 1992; Greensmith et al., 2004)，而不是学习规则本身的问题(请参见"材料和方法")。请注意，过度降低学习率会导致学习该任务所需的尝试次数急剧增加。因此，较小的成功偏移对于R-max而言是有利的，因为它使系统能够更快地学习任务，但这不是必需的。如下所示，R-STDP并非如此。
Small success offsets turn reward-based learning into unsupervised learning
对于具有有限偏差<eij>的学习规则，学习包括学习的奖励敏感成分(即等式17中的协方差项Cov)和无监督偏差
之间的权衡。因为成功偏移
是一个折衷的参数，所以我们认为它应该对学习性能有很大的影响。我们使用R-STDP (Farries and Fairhall, 2007; Izhikevich, 2007; Legenstein et al., 2008)(一种常见的STDP奖励调节版本)检验了该假设(请参见"材料和方法")。图2A显示，成功信号的SD(σR)幅度为25％的成功偏移足以防止R-STDP响应给定的输入脉冲模式学习目标脉冲序列。此外，对于成功偏移
(即平均成功信号为负)(图2A，绿点)，学习后的性能甚至低于学习前的性能(图2A，水平虚线)。因此，R-STDP不仅无法学习任务，有时甚至会导致任务的学习失败。与R-max相反，R-STDP不能通过学习率的降低来挽救(图2A，空心圆圈)，这表明这不是噪声问题。
然后，我们检查了这种失败是否确实是由无监督偏差引起的。在无监督的情况下，已经证明，如果重复出现相同的输入脉冲模式，STDP通过逐渐减少第一个输出脉冲的延迟，使突触后神经元尽早发放(Song et al., 2000; Gerstner and Kistler, 2002; Guyonneau et al., 2005)。因此，我们将学习后的第一个输出脉冲的延迟与目标模式的第一个脉冲的延迟作图。图2B显示，根据成功偏移
，R-STDP系统地导致短时延(
，STDP的偏差占优势)，长时延(
，反STDP的偏差占主导)或所需的目标延迟(
，偏差可忽略不计)。R-max学习规则不存在成功偏移的这种影响（图2C），因为它没有无监督的偏差。
R-STDP对成功偏移的强烈敏感性不是R-STDP特定模型的特性，而是通用的。对于权重依赖的STDP模型，性能仍然一样低(van Rossum et al., 2000)(图2D)，并且不能通过更改STDP的pre-before-post与post-before-pre窗口之间的平衡来提高性能(图2E)。有趣的是，只要成功偏移消失(C/σR = 0)(图2D, E)，学习对STDP模型的细节就相对不敏感，尽管在没有post-before-pre部分的情况下性能会略好一些(λ = 0)。
我们的结论是，独立于模型的细节，R-STDP保持一种无监督偏差，因此，在大多数奖励学习任务中都会失败，除非成功偏移
很小。
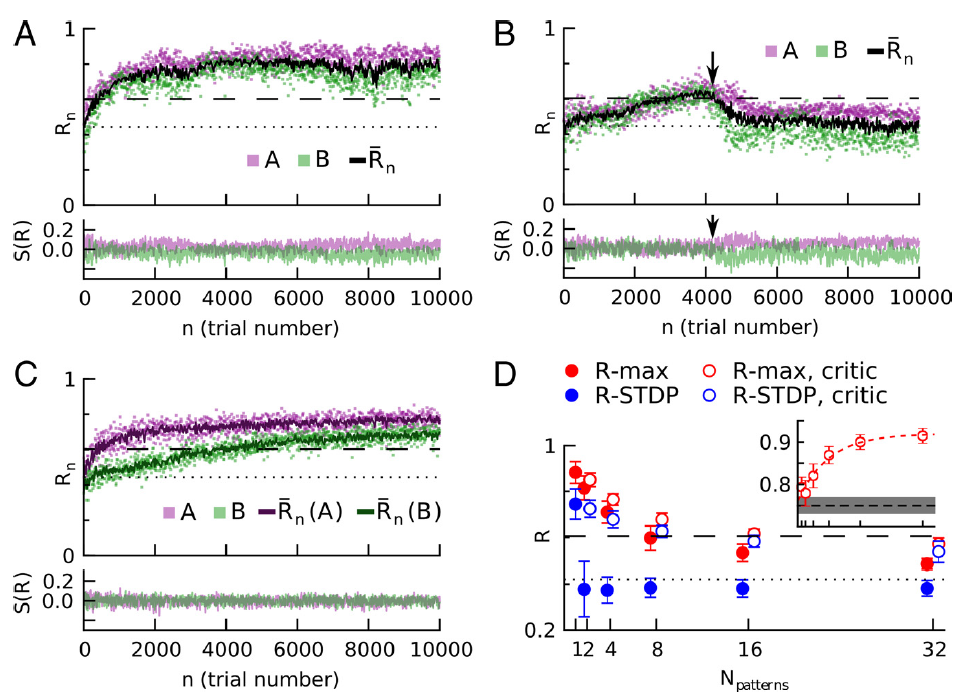
图3. R-STDP，而不是R-max，需要特定于刺激的奖励预测系统，以学习多种输入/输出模式。在每次试验中，模式A或B都会出现在输入中，并将输出模式与相应的目标模式进行比较。A，R-max可以学习两个模式，即使每个模式的成功信号S(R)不平均为零。顶部，奖励是试验编号的函数。洋红色，图案A；绿色，图案B；黑色，奖励的运行试验均值；点线，学习前奖励；虚线，使用参考权重获得的奖励(请参见"材料和方法")。底部，刺激A和B的成功信号S(R)。为清楚起见，仅显示了25％的试验。B，如果成功信号不是特定于刺激的，则R-STDP无法学习两种模式。只要有机会，刺激A和刺激B的实际奖励是相似的[前4000个试验；A(洋红色)和B(绿色)奖励值重叠]，则平均奖励减法对于这两者都是正确的，并且性能会提高。但是，一旦在两个任务之间出现平均奖励的微小差异(～4000次试验中的箭头，绿色点上方的洋红色)，性能就会下降到学习前的水平(点线)，并且无法恢复。为了清晰起见，该图显示了失败相对较晚的试验。C，如果成功信号是刺激特定的奖励预测误差，则可以挽救R-STDP。critic维护特定于刺激的平均奖励预测变量(顶部，深品红色和深绿色线)，并为网络提供两种刺激的无偏成功信号(底部)。D，性能随刺激次数的变化。刺激特定的奖励预测系统对大量不同的刺激-响应对产生显著影响。实心圆圈，基于简单且无刺激性的试验均值得出的成功信号；空圈，特定刺激的奖励预测误差。R-STDP(蓝色)在没有特定于刺激的奖励预测的情况下，无法学习多个刺激/响应关联，但在带critic的情况下性能良好，保持接近参考权重的性能水平(虚线)。R-max(红色)不需要刺激特定的奖励预测，但可以提高性能。带有/不带有critic的点水平偏移以提高可见性；它们对应于横坐标的刻度。对于大量的刺激/响应对，性能会下降，因为随着学习的权重变得越来越不专业，并且更接近参考权重(请参见插图)，参考权重的性能将成为性能上限。插图，学习权重和参考权重的归一化标量乘积
(显示在垂直轴上，水平轴显示与主图相同的值)。仅显示带critic的R-max数据。红色虚线，数据的指数拟合。黑色虚线和灰色区域分别代表随机均匀绘制的权重
的均值和SD。在所有面板中(D的插图除外)，虚线表示学习之前的性能，而虚线表示参考权重的性能。
Reward-based learning with biased rules requires a stimulus-specific reward-prediction system
原则上，如果平均成功信号为零，例如，如果神经调节成功信号不是奖励本身，而是奖励减去期望奖励
，则可以实现小的成功偏移
。到目前为止，成功偏移是通过从实际收到的奖励R中减去奖励的试验均值
来减少的。我们现在讨论的问题是，在需要学习多个任务(或者，在这种情况下，刺激/反应关联)的场景中，这种方法是否也足够。下面的论点表明情况并非如此。假设有两种刺激，在随机交叉试验中出现的概率相等，并且每种刺激都与不同的靶点相关。假设，对于当前的突触权重，刺激A导致平均奖励
，而刺激B导致平均奖励
。奖励的试验均值由
给出(按随机顺序计算为大量试验任务A和B的均值)。如果我们现在根据等式17考虑由对应于任务A的刺激子集引起的平均权重变化，我们会发现成功偏移
(以刺激A为条件)由下式给出：
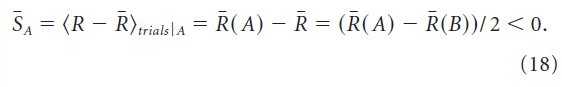
因此，刺激A的平均权重变化包含一个偏差分量。刺激B的平均权重变化也是如此，但偏差的作用方向相反，因为成功偏移SB，以刺激B为条件，平均为正。由于偏差项对两种刺激的反应产生相反的影响，平均奖励的微小差异R(A) - R(B)被放大，偏差的影响增加，学习失败(图3B)。因此，除非每个刺激的成功偏差量分别消失，否则不能用有偏学习规则学习多个刺激。
我们想知道一种更先进的计算成功信号的方式是否有助于解决上述多任务问题。上一段的论点表明，我们必须要求每个刺激的成功偏差量分别消失。为了实现这一点，我们考虑了一个成功信号，它模拟了一个特定于刺激的奖励预测误差，即实际提供的奖励和该刺激的奖励预测之差。为了预测期望奖励，我们使用了最近每个任务的平均奖励。我们通过分别对任务A和B进行试验的均值来计算平均奖励RA和RB。我们称识别刺激、减去和更新刺激特定平均奖励的系统为critic，因为它与强化学习的critic相似(Sutton and Barto, 1998)。通过这样的设置，R-STDP同时学习两个任务(图3C)。此外，如果选择的任务都可以使用相同的权重集来实现(参见"材料和方法")，则具有critic的网络可以使用R-STDP同时学习至少32个任务(图3D)。对于一个以上的模式，无critic的R-STDP性能较差；其性能低于具有固定且均匀权重的网络(图3D，水平虚线)。critic还改进了R-max的性能，因为它减少了权重变化的试验总变异性(参见"材料和方法")。因此，如果必须同时学习多个任务，则无论学习规则如何，实现依赖于刺激的奖励预测的critic都是有利的。此外，无论任务数多少，带critic的R-max总是比带critic的R-STDP好，尽管随着任务数的增加，优势变小。关于赞成和反对大脑中存在critic的论点，请参见"讨论"。
图4. 将结果应用于更现实的时空轨迹学习任务。学习设置在几个方面与图1有所不同。A，随机输入。输入的发放率是固定数量的随机分布高斯的总和。在试验过程中，发放率(有色区域)是恒定的，但每次试验的脉冲序列都不同(黑色脉冲)。任务A和B随机交织。在执行任务A和B时都会发放一部分输入，其他神经元仅针对特定任务发放。网络结构与图1相同，但具有350个输入和200个神经元。B，群体矢量编码。对输出神经元的脉冲序列进行滤波，以产生突触后频率ri(t)(左上方)。每个输出神经元都有一个首选方向，
(右上)；实际的运动方向是群体矢量
(右下)。神经元的首选方向随机分布在三维单位球体上(左下)。C，奖励调节STDP可以学习时空轨迹。网络必须响应两个不同的输入来学习两个目标轨迹(红色轨迹)。目标轨迹A在xy平面中，而B在xz平面中。绿色和蓝色轨迹分别显示了任务A和B的最后一次试验的输出轨迹。灰色阴影表示轨迹相对于其各自目标平面的偏差。该网络使用了带critic的R-max学习规则，进行了10000次试验。D，奖励是根据学习轨迹与目标轨迹之间的差异计算得出的。该图显示了实际运动方向和目标方向的标量乘积，该乘积是在模拟的最后20次试验中平均得到的；更高的价值代表更好的学习。在试验结束时给予的奖励是该标量乘积的正数，在整个试验中平均为
。E，脉冲序列学习实验的结果适用于轨迹学习。条形图代表最近100次试验的平均奖励(整个学习序列的10000次试验)。误差线显示了20种不同轨迹对的SD。每个学习规则都在以下三种设置中进行了模拟：带奖励预测系统的随机交替任务(critic)，无critic的500个试验块中的交替任务(块)和无critic的随机交替任务(rand.)。阴影线表示没有post-before-pre窗口的R-STDP，对应于图2E中的λ = 0。虚线表示学习之前的性能。
Results apply to a spatiotemporal trajectory learning task
刻板动作序列的程序学习包括慢动作(如上班途中"在面包店右转")，以及需要一秒钟或更短时间的快速而精确的动作序列。例如，在乒乓球比赛的发球过程中，职业运动员在击球前用球拍快速移动，试图掩盖球的旋转和方向。同样，在同声传译过程中，口译员从口头语言到手语都会以高时间精度进行复杂的动作。在这两个例子中，这些运动都是经过数百次，甚至数千次的试验学习和实践的。动作本身是定型且快速的，不需要视觉反馈，是作为一个单一序列来执行的。
我们想知道，一个由脉冲神经元组成的网络，原则上是否可以学习如此快速的时空轨迹。轨迹表示为时空脉冲模式，类似于图2和图3以及最后一秒中使用的模式。将脉冲与轨迹联系起来的代码受到了群体矢量方法的启发，该方法已成功地用于解码灵长类动物的运动意图(Georgopoulos et al., 1988)。神经元的每一个输出脉冲都决定了神经元的运动方向。将所有输出神经元的贡献相加，得到轨迹的归一化速度矢量。我们的模型网络学习的目标是在空间中产生两个不同的目标轨迹，使用一个范例，在每个试验结束时给出一个标量成功信号。奖励表示网络产生的轨迹与给定试验的目标轨迹之间的相似性。和以前一样，奖励作为一个全局信号传递给所有的突触。
网络和学习过程与图2和图3相同，只是有三点是为了更真实(参见"材料和方法")如下：输入是随机的(图4A)，网络更大(350个输入神经元和200个输出神经元)，成功信号来自轨迹不匹配，而不是脉冲时间不匹配(参见"材料和方法")(图4B)。
我们发现，网络可以学习相当精确地重现目标轨迹(图4C, D)。与我们对图2和图3的学习任务的结果一致，R-max不需要critic (尽管它提高了R-max的性能)，而R-STDP需要critic来解决问题(图4E)。与图2E的结果类似，对于post-before-pre时序(λ = 0)，不带LTD的R-STDP的性能优于平衡R-STDP (λ = -1)，其性能与带critic的R-max相当。总之，无论学习窗口的确切形状如何，R-STDP都需要一个critic。
如果任务在500个试验块内保持不变，则任务特定的奖励预测系统(由critic实现)可以由更简单的奖励试验均值代替(图4E)组间间隔显著大于奖励预测系统的平均时间常数。基于块的学习和critic的学习一样好(图4E)的发现在一般情况下可能是正确的，因为在块学习范式中，简单的运行均值有效地模拟了critic。
Discussion
在这篇文章中，我们问在什么条件下，奖励STDP适合学习奖励行为，即最大化奖励。为此，我们分析了一类相对广泛的具有乘法奖励调节的学习规则，其中包括最近提出的大多数基于脉冲的奖励调节突触可塑性计算模型(Xie and Seung, 2004; Pfister et al., 2006; Baras and Meir, 2007; Farries and Fairhall, 2007; Florian, 2007; Izhikevich, 2007; Legenstein et al., 2008; Vasilaki et al., 2009)。分析表明，学习动力由无监督偏差和基于奖励的学习之间的竞争构成。平均调节成功信号作为无监督和基于奖励的学习之间的权衡参数。尽管这开启了一个有趣的可能性，即大脑可以通过控制单个参数(相当于成功偏移)在无监督和奖励学习之间进行改变，它为有效的奖励学习引入了一个相当严格的约束条件：R-STDP的模拟结果表明，平均成功率与零的微小偏差会导致无监督偏差占主导地位，阻碍了在学习过程中增加奖励的目标。
我们认为有两种方法可以解决偏差问题。第一种方法是从奖励学习规则中去除无监督倾向，从而使其对无监督任务无效。这就是R-max学习规则的原理，对于本文中的所有模拟实验，它产生了最好的或共同最好的学习结果。第二种解决方案是使用刺激特异性奖励预测误差(RPE)作为成功信号。换句话说，神经调节成功的信号不是奖励本身，而是奖励与刺激期望奖励之差。第二种解决方案似乎有两个原因：它与强化学习中的TD学习相一致(Sutton and Barto, 1998)，因此，它符合皮质下多巴胺信号作为RPE的有影响力的解释(Schultz, 2007, 2010)。目前尚不清楚多巴胺神经元或其他一些回路是否以及如何计算刺激特异性RPE。以下各段将讨论这些要点。
Relation to TD learning
与我们的方法类似，TD学习依赖于RPE，即实际获得的奖励R和动物平均期望奖励的内部预测
之差。然而，我们对RPE的定义与TD学习中的定义略有不同。特别地，预测
的计算是不同的。在我们的方法中，它是给定输入脉冲序列和当前权重配置的平均奖励的内部估计。先验地，这个定义不需要时间预测。它唯一的功能是中和学习规则中的无监督倾向。在TD学习中，奖励预测信号是两个后续状态之间的差值，其中该值指示从该状态开始时在未来期望的奖励量。这种时间奖励预测中的系统误差具有向后传播延迟奖励信号信息的功能。TD学习是由奖励预测中的系统性误差(即成功偏移)驱动的，这些误差的消失表明状态价值与当前策略是一致的。相反，对于奖励调节STDP，系统的RPE产生了无监督偏差，因此对学习有害。换句话说，如果平均RPE消失，这是TD学习学会该任务的信号，而对于奖励调节STDP，这是它现在可以开始学习的信号，不受无监督倾向的阻碍。对R-STDP的精确奖励预测的要求是R-STDP的一个严重障碍，在克服偏差问题之前，需要对其进行学习。
What is the success signal?
成功信号的候选者是神经调节剂，如多巴胺和乙酰胆碱(Weinberger, 2003; Froemke et al., 2007)。成功信号编码RPE而非仅奖励的要求与基底节多巴胺能神经元的反应模式一致(Schultz et al., 1997, 2007)。此外，通用突触可塑性(Reynolds and Wickens, 2002; Jay, 2003)和特殊STDP (Pawlak and Kerr, 2008; Zhang et al., 2009)受到多巴胺能调节。
How can the critic be implemented?
刺激特定的RPE需要一个奖励预测系统，一个强化学习语言中的critic，因为期望奖励需要为每个刺激分别预测。我们通过使用简单的试验均值在算法上绕过了这个问题，因为我们的主要目标是证明这种系统对于R-STDP是必需的，对于R-max是有利的，而不是提出可能的实现。
尽管大脑中RPE的存在已被广泛认同，但RPE的计算方法以及它们适应不断变化的实验条件的生理机制的生物学基础仍不清楚。即便如此，critic的神经网络实现已经被提出使用TD方法(Suri and Schultz, 1998; Potjans et al., 2009)，表明训练critic是可行的。事实上，考虑到本研究中所做的轨迹学习需要估计具有～100个自由度(～50个时间点 x 2个极坐标角)的轨迹，学习期望奖励(单个自由度)，即critic的任务，比学习沿轨迹的运动更简单。
大脑用来训练critic的确切的学习方案是未知的，但它不能涉及R-STDP。这是因为，正如我们在本文中所展示的，R-STDP需要一个RPE系统，但是在critic被训练之前，RPE是不可用的。
Can block learning replace the critic?
从人类的心理物理学来看，一次学习几个任务比一次学习一个任务更具挑战性(Brashers-Krug et al., 1996)。这一观察结果可以解释为奖励预测系统缺陷的结果。事实上，在一个不平衡的学习规则中，一个可能的解决方案是限制学习范式。在这种情况下，依赖于刺激的奖励预测系统(critic)可以被一个更简单的奖励平均系统所取代，该系统在大多数情况下将平均成功信号平衡为零(因为刺激很少改变)。然而，很可能还涉及其他影响，如第二个任务对第一个任务的整合的干扰(Shadmehr and Holcomb, 1997)。
Is STDP under multiplicative reward modulation?
我们研究了一类学习规则，包括R-STDP和R-max。这两种规则都依赖于突触前和突触后脉冲的相对时间以及成功的奖励编码信号的存在。此外，R-max取决于瞬时膜电位。这些规则在生物学上是否合理？
R-STDP已经实现为标准STDP规则，由成功信号进行乘法调节。这意味着只有当成功信号为正时(例如，如果奖励大于期望奖励)，间隔几毫秒的pre-before-post发放序列才会导致增强。如果成功信号为负，同样的序列会导致抑制。类似地，成功信号的标志决定了post-before-pre发放序列是否会抑制或增强R-STDP，但我们已经看到，post-before-pre发放序列没有可塑性的模型与正常的R-STDP工作得一样好，甚至更好。
R-STDP部分符合皮质性STDP的特性，LTP和LTD都需要激活多巴胺D1/D5受体(Pawlak and Kerr, 2008)。然而，同样的研究表明，乘法模型过于简单化，因为D2受体的激活不同地影响了脉冲时序依赖性LTP和LTD的表达时间过程。因此，可塑性的量不能分解为STDP曲线和决定STDP幅度的乘法因子。另外，最近在海马细胞培养中的另一项研究表明，多巴胺水平的增加可以将STDP的LTD(post-before-pre)成分转化为LTP，而LTP(pre-before-post)成分在振幅上保持不变，但改变其符合性要求(Zhang et al., 2009)。在STDP与其他神经调节剂的相互作用中也观察到了类似的效果(Seol et al., 2007)。未来的R-STDP模型应该考虑这些非线性效应。我们分析的基本结果很可能继续适用于更复杂的R-STDP模型。无监督偏差反映了当成功信号(如多巴胺浓度)取其均值时，STDP对突触权重的平均影响。为了使奖励最大化，当成功信号反映出意外的奖励存在或不存在时，无监督偏差应该可以忽略不计。相应的实验预测是，在被认为参与奖励学习的大脑区域，STDP应该不存在基准多巴胺水平。
如上所述，反对R-STDP(或反对任何基于有偏无监督规则的奖励调节可塑性规则)的一个重要论点是，它需要一个critic为它提供刺激特定的RPE，然而R-STDP不能用来训练critic。如果critic用另一种学习方案(例如TD学习或无监督的STDP将奖励结果与刺激联系起来)学习，这个"鸡和蛋"的难题就可以解决，但它仍然代表着对R-STDP的生物学合理性的强烈打击。相比之下，像R-max这样的无偏学习规则是自洽的，在这个意义上，相同的学习规则既可以被实际的学习者使用，也可以被critic用来改进前者的性能。
R-max是一个规则，它依赖于脉冲时序和奖励，但也依赖于膜电位。它最吸引人的理论特点是，增强和抑制本质上是平衡的，所以它的无监督偏差消失。这种平衡来自这样一个事实：对于一个恒定的奖励，抑制量随着膜电位的增加而增加，而在pre-before-post序列中的突触后脉冲引起增强。由于发放脉冲的概率随着膜电位的增加而增加，所以这两个项，抑制和增强，相互抵消。事实上，实验定性地表明，在阈下区域，抑制随着突触后膜电位的增加而增加，而在膜电位区域，增强是主要的，通常发生在脉冲期间(Artola et al., 1990)。此外，重复的pre-before-post时间序列会产生增强作用，如许多STDP实验所示(Markram et al., 1997; Sjöström et al., 2001)。然而，目前尚不清楚的是，对于每一个未受到奖励的自然刺激，突触可塑性的电压依赖性是否被调节到LTP和LTD完全相互抵消的程度。这将是将任何无监督偏差归零的技术要求。我们的结果表明，如果规则的无监督偏差不平衡为零，则需要一个奖励预测系统将成功信号平衡为零均值。
我们的结果可以通过列出奖励调节STDP的功能需求来总结。非监督学习规则需要一些微调，以保证任何刺激的LTP和LTD之间的平衡(这是R-max的解决方案)，或者如果我们对每个刺激的可能结果进行平均，则奖励必须作为一个平衡到零的成功信号来给予(此解决方案由一个带critic的系统实现)。第二种选择要求使用另一种学习方案来解释critic的RPE学习。
Rate code versus temporal code
我们的主要理论结果不依赖于特定的学习规则和神经元所使用的编码方案，无论是频率编码还是时序编码。我们重点研究了由成功信号调节的基于脉冲的奖励可塑性规则的变体。然而，公式17中的数学论证结构表明，如果经典的基于频率的赫布可塑性模型[例如，BCM规则(Bienenstock et al., 1982)或Oja规则(Oja, 1982)]辅之以调节因子编码成功，则其主要结论也适用。此外，即使使用基于脉冲的可塑性规则，如果成功信号仅取决于脉冲计数而不是脉冲时序，我们也可以实现频率编码方案。我们在图2, A和F中的模拟显示了脉冲时序和频率编码范式的相同结果。
对于图4中的轨迹学习任务，我们认为运动区域(如运动皮层)的运动编码依赖于精确脉冲时序，大约20毫秒。神经假体的经典实验(Georgopoulos et al., 1986)，实验人员试图读出猴子的皮层神经活动来预测手部运动，由相对缓慢和均匀的运动组成。例如，在中心向外伸展的任务中，相关的奖励信息是最终位置，因此只有手运动的平均方向才是重要的。在此设置中，简单的频率编码方案(>100 ms时间单元)可能就足够了。然而，即使在这种情况下，通常也会使用20毫秒范围内的较小时间段(Schwartz, 2004)。我们认为，对于运动所需的更快和更精确的运动，或者对于猴子自然环境中进食任务的子集，运动区域可能存在时间精度在20ms范围内的更精确的时序编码方案。这种码可以是快速调节频率码(例如，以约10 ms的精度调节神经元群体中的发放概率)或时空脉冲码。在我们的模拟中，运动被编码成脉冲时间，用一个持续时间为20 ms的滤波器进行卷积。这样的编码方案可以被解释为脉冲码或快速调节频率码(该项没有很好地定义)，但是在20 ms的时间尺度上的时间精度与编码1 s持续时间的复杂轨迹有关。
Limitations
在众多依赖于脉冲时序和奖励的规则中，R-max是理论上最理想的规则。我们发现它比一个简单的R-STDP规则要好，在某些情况下，甚至比带critic的R-STDP规则还要好。这样一个能够预测期望奖励的critic如何在自然界得到实现，目前尚不清楚。
我们强调，我们并不是说有限成功偏移的R-STDP不能学习一般的奖励行为。相反，我们讨论了R-STDP是否总是最大化奖励的问题，即它是否能够解决广泛的任务。例如，如果任务是学习状态细胞和动作细胞之间的突触权重，例如，指示动物的位置，其中活性最高的细胞决定下一个动作，赫布学习规则的潜在无监督偏差将在(稀疏发生的)奖励条件下加强状态-动作对的正确关联(Vasilaki et al., 2009)。然而，它这样做只是因为编码方案(更高的活动 → 选择一个动作的更高概率)是符合无监督偏差。在更复杂的编码方案(群体编码、时序编码)中，很难确定学习规则和给定的编码方案是否协调。
最后，很明显，去除学习规则中的无监督偏差，无论是通过使用RPE还是通过无偏学习规则，都不能保证系统学习到奖励行为。一个说明性的例子是R-max规则的负版本，它与R-max本身一样无偏，但是最小化收到的奖励。奖励调节可塑性的实验形式是否能提供成功学习的任务和编码方案还有待研究。