郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！
PloS one, no. 9 (2011): e22885-e22885
Abstract
对构建稳定循环模型网络的标准理论方法的主要批评是，需要对突触连接权重进行微调。这种批评之所以严峻，是因为有关学习这些权重的建议规则已显示出对其生物学合理性的各种限制。因此，不太可能使用此类规则在体内连续微调网络。我们描述了一种能够以生物学合理的方式调整突触权重的学习规则。我们在动眼积分器的背景下演示并测试了该规则，表明仅需要已知的神经信号即可调整权重。我们证明了该规则适当地说明了各种各样的实验结果，并且在几种扰动下具有鲁棒性。此外，我们表明，该规则能够获得与积分器循环模型中经常使用的线性最优权重所提供的稳定性相同或更高的稳定性。最后，我们讨论了如何将这一规则推广到各种各样的循环吸引子网络上，例如在头部方向和路径整合系统中发现的那些，表明它可以用于调节各种各样的稳定神经系统。
Introduction
Materials and Methods
The optimal neural integrator
Derivation of optimal decoders
Derivation of the learning rule
神经积分器的可塑性在各种各样的物种中都很明显，并且有强有力的证据表明，修改视网膜滑移信息能够使动眼积分器变得不稳定或受阻[19,30]。调整在人的动眼神经积分器中的作用的其他支持来自出生后两个月内调整的证据[41]，患有失明的受试者的错误调整[42]以及训练后诱发的漂移[43]。虽然来自黑暗饲养动物的实验证据显示了没有视觉反馈的积分器的发展[25,26]，但当向动物提供视觉反馈时，眼部稳定性会提高。因此，有充分的证据表明某种形式的适应在眼动积分器中是活跃的，并且这种适应可能能够支持微调是合理的。
这项研究的目的是确定能够执行整合以及上述线性最优网络的生物学可行的学习规则。此处得出的学习规则基于这样的思想，即积分器应该能够利用其接收到的校正输入信号。经验证据表明，积分器本身的所有输入均采用速度指令的形式[44]。虽然视神经道核具有视网膜滑移信息，但当它投影到神经积分器时，它会将其编码为速度信号[45]。因此，没有过去的学习规则所假定的明确的视网膜滑移信号[24,23]。
在动眼积分器中，有两类输入的证据：故意扫视和矫正扫视[46,47]。[48]认为矫正扫视而不是明确的视网膜滑移误差会引起扫视幅度的适应。扫视命令有几个特征，可用于区分矫正扫视和故意扫视，包括速度大小或位置变化(见图2)。由于眼睛通常在矫正扫视的目标附近，因此矫正扫视速度趋于变小。而且，由于扫视幅度与最大扫视速度成正比[49]，因此有可能根据幅度过滤扫视速度命令，以识别校正扫视。在此模型中用于过滤扫视速度vs给出校正扫视vc的算法为：
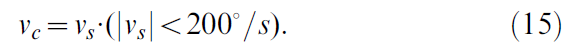
即，校正扫视信号由每秒小于200度的所有速度组成。
此外，[27]解释说，单独的视网膜滑移不能解释在黑暗中的学习，也不能吸收本体感受反馈，这在长期调节眼控方面具有一定作用[50]。基于矫正速度信号的算法具有与视网膜滑移，传出反馈和本体感受反馈一起工作的潜力，因为这些中的任何一个都可能驱动矫正眼球运动。 已知在黑暗中会发生小的校正扫视[51]。
尽管如此，视网膜滑移在整个系统中仍起着重要作用。 在大多数动眼系统模型中，包括我们在下面采用的模型，都会根据视网膜滑动信息生成矫正扫视。 如果视网膜图像在移动，但是没有自生运动(即，视网膜图像是"滑移")，则系统将生成校正速度命令以消除滑移。因此，积分器本身只能间接访问视网膜滑动信息。下面，我们证明这足以驱动适当的学习规则。
在转向规则本身之前，先考虑一下必须对系统进行微调的主张是有用的。当来自反馈连接的电流之和等于精确表示开环系统中眼图位置所需的电流量时，积分器能够维持持续的活动。如果将由反馈电流确定的眼图位置和实际眼图位置绘制在归一化轴上，则理想积分器的映射将定义一条通过原点的斜率线(见图3)。该行称为系统传递函数，因为它描述了如何将当前状态(通过反馈)转换为将来的状态。因此，神经积分器中的斜率1表示重复输入在任何给定的眼睛位置产生的电流正好足以弥补通过神经元膜的正常电流泄漏。简而言之，这意味着网络已经实现了完美的线吸引子。
但是，如果反馈的幅度小于所需的幅度，则表示的眼睛位置将向零漂移。这由系统传递函数的斜率小于1表示。这种系统据说是动态阻尼的。相反，如果反馈大于所需的反馈，则传递函数的斜率大于1，系统输出将偏离零。据说这种系统是动态不稳定的(参见图3)。
如前所述，等式8给出的眼睛位置表示具有一定的误差(对于图1所示的神经元，RMSE为0.134度)。因此，并非在所有眼睛位置都可获得完美的吸引子(斜率为1)。然而，从线性最优积分器的推导中可以清楚地看出，改变解码权重di(因此，连接权重wij = ajejdi)等同于改变网络中眼睛位置的代表值。因此，改变这些权重将使我们或多或少准确地近似一个精确的积分器。
在这种背景下，有可能得出一种学习规则，该规则将眼睛位置
的神经表示与实际位置x的差异最小化。重要的是，可用的校正扫视vc提供有关最小化方向的信息。具体而言，如果vc为正，则必须增加估计值，以趋于x；如果vc为负，则必须降低估计值。更正式地讲，我们可以将要最小化的误差表示为：
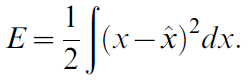
将等式8中的神经表示代入该表达式，然后通过对di给出的解码权重进行微分来最小化它：
其中下标 j 表示整个群体，i 表示当前正在优化的神经元。然而，请注意，在一个循环网络中，i 和 j 是同一个神经元的索引。此外，依赖于 i 的连接权重存在于突触后神经元 j 中。因此，尽管该等式被写成 i 的优化，但由此产生的学习规则用于调整 i 投影到的神经元 j 中的权重。
重要的是，现在可以用纠正性扫视的负数来代替括号中的项。之所以可以进行这种替换，是因为vc是由动眼神经系统产生的，以便与由该项表示的差异(即，实际的和表示的眼睛位置之间的差异)成比例，但方向相反。执行此替换将得到：
将其转换为标准的delta规则形式，并包括学习率参数κ，给出：
此规则指示解码器本身应如何更改以最小化误差。
不幸的是，该规则既不是关于电路的连接权重，也不是局部的。可以通过将等式的两边乘以神经元 j 的编码器和增益来缓解这两个问题，神经元 j 从神经元 i 接收投影：
等式17中的最终学习规则解决了这两个问题。首先，连接权重的NEF表征可确保在给定项定义(如等式9中得出)的情况下，用vij代替diejαj是合适的。
其次，等式17的右侧为伪Hebbian形式：学习率κ，突触前活动ai和突触后活动αjejvc。最后一项是矫正扫视对突触后神经元 j 的体细胞电流的影响，如等式7所述。值得注意的是，该项不是接收神经元的发放，而是驱动该发放的亚阈值电流(因此是"伪"Hebbian)。换句话说，用于驱动神经元的脉冲活动的相同电流用于更新连接权重。与该规则一致，在实验工作中已经提出，突触后电位对于可塑性不是必需的[52]。
（略）
Generalization of the learning rule
The oculomotor system model
Simulations
Measuring drift
Results
Application of the learning rule to the oculomotor integrator
Application of the generalized learning rule
Discussion
Optimality of linear methods
Empirical consequences
The generalized learning rule