郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！
Encyclopedia of Computational Neuroscience, (2014)
Definition
RL代表AI和生物学学习的基本范例。该范式考虑了一种在典型的随机环境中采取动作并在达到某些状态时获得奖励的智能体(机器人，人类，动物)。智能体的目标是通过在任何给定状态下选择最优动作来最大化期望奖励。在皮层实现中，状态由馈入神经元网络的感觉刺激来定义，在网络活动稳定后，读出动作。学习包括基于有关所选动作的适当性的(通常是二值的)反馈，使突触连接强度适应神经元网络的内部。策略梯度和TD学习是两种用于导出突触可塑性规则的方法，该规则可使响应刺激的期望奖励最大化。
Detailed Description
为了使期望奖励R最大化，考虑不同的方法来调整突触权重w。通常，权重适应具有以下形式：
其中R = ±1编码选择的动作后获得的奖励，PI表示突触基于突触前和突触后的活动计算的可塑性诱导。为了防止不是由奖励和可塑性诱导的共同变化引起的突触权重的系统性漂移，平均奖励或平均可塑性诱导必须消失，即<R> = 0或<PI> = 0。
RL可以分为两个不是互斥的类别，这些类别假设(A) <PI> = 0或(B) <R> = 0。第一个类别包含策略梯度方法，而另一个更广泛的类别包含TD方法。策略梯度方法采用较少的结构，因为它们在可塑性适应的动作选择模块的相同突触上假设所需的属性(<PI> = 0)。TD方法还涉及内部批判的适应，因为它们必须确保调节信号(<R> = 0)的所需属性分别适用于每种刺激类别。
A) Policy gradient methods
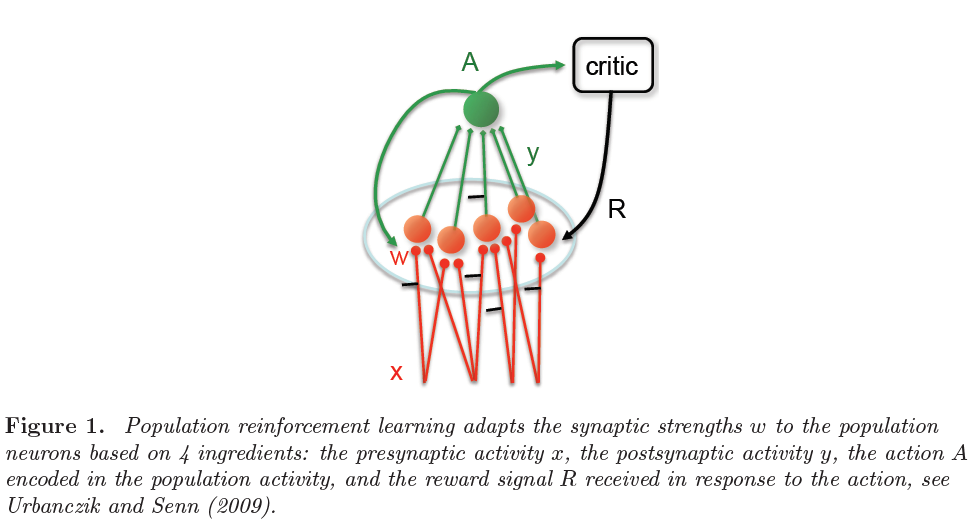
在最简单的生物学合理的形式中，动作由神经元的群体活动表示。群体中的每个神经元都由编码当前刺激的前馈输入来突触式驱动(图1)。根据所有可能动作的期望奖励的梯度来调整突触强度。从估计该梯度的不同方法中涌现出各种学习规则。
用正式的术语来说，感觉刺激定义为输入x，例如脉冲序列被馈送到以突触强度w为特征的网络。该网络生成输出y，也就是脉冲序列，它取决于突触权重w和输入x。基于y，选择一个动作A(图1)。最终，该动作将通过典型的二值信号R(x, A) = ±1获得奖励，该信号被反馈回网络，在网络中它通过全局因子来调节突触可塑性。刺激选择，网络活动和动作选择可能具有随机成分。指定在输入x时选择动作A的概率函数Pw(A|x)称为动作策略。策略梯度法考虑期望奖励：
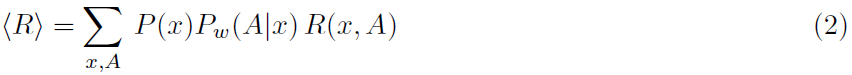
并沿奖励梯度调整突触连接强度w，即使得期望的权重变化满足
且学习率η很小但为正(Williams, 1992)。
Hedonistic synapse 在当前形式下，假设使用突触来估计w的变化如何影响概率Pw(A|x)。但是此信息可能在单个突触处不可用。根据享乐主义突触模型(Seung, 2003)，仅假设突触能够访问非常局部的信息，以了解在 t 时刻是否存在释放(rt = ±1)以响应突触前脉冲，并且xt本身编码突触前脉冲的存在或不存在。然后，我们可以写出Pw(A|x) = ∑r P(A|r)Pw(r|x)，其中Pw(r|x)由变量w参数化，并且总和取自所有释放序列r。将其插入(2)并取我们得到的导数：
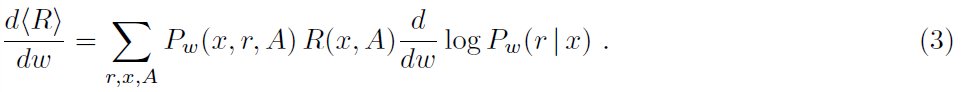
对梯度进行采样会导致在响应突触前脉冲序列而采取动作A后更新w，
注意在任何情况下
，因为
且因此<PI> = 0，如等式1之后所述。
为了从(5)获得一个在线规则，一个低通滤波器
来获得一个资格迹，然后将其乘以R以计算突触更新(Seung, 2003)。如果为简单起见，我们认为发生突触前脉冲的单个时间间隔并采取动作，则规则(5)变为：
其中p = Pw(r = 1 | x = 1)是释放的概率，它由w的sigmoid函数参数化，p = 1/(1+e-w)。在一般情况下，可塑性诱导PI = (r - p)x是低通滤波的，其时间常数反映了奖励延迟(请参见下面的在线学习)。
Spike reinforcement 由于特定的突触释放与动作奖励之间几乎没有相关性，因此估计梯度
的更有效方法是考虑A对y的依赖性，如
所示。再次将其插入(2)中并获取采样版本的导数：
该突触可塑性规则取决于三个因素，(i) 奖励，(ii) 突触后量(在此被视为一个因素)和(iii) 突触前活动。对于脉冲神经元，Xie and Seung (2004)引入相应的学习规则，Pfister et al. (2006); Florian (2007); Frémaux et al. (2006)对其进行进一步研究。
Node perturbation 在脉冲神经元的框架中，对神经元状态空间的探索由单个神经元脉冲机制中存在的固有噪声驱动。如果噪声是从外部来源进入的，因此可以进行显式调整，则可以进行更有效的探索。这个想法导致了基于节点扰动的RL (Fiete and Seung, 2006)。在上面考虑的简单编码方案中，节点扰动在形式上等效于(7)，并且可以使用ξ = y - Φ重写为：
然而，节点扰动也可以推广到由常规"学生"输入和"探索"输入驱动的基于电导的神经元，并且像以前一样，可塑性诱导PI = ξΦ'x可以再次由遵守奖励延迟的低通滤波代替(Fiete and Seung, 2006)。
Population reinforcement 当假设突触可以访问选择动作A所涉及的下游信息时，例如通过全局神经调节剂，可以通过直接计算(2)相对于w的导数来很好地估计梯度。然后，此规则的采样版本为：
该动作本身可以是二值的，例如取决于大多数群体神经元是否对刺激发放脉冲(Friedrich et al., 2011)，或者这也可以是连续的，例如取决于平均群体发放率(Friedrich et al., 2014)。
请注意，与(5)和(7)的形式相似之处是，后者中的"探索项"(y - Φ(u))现在被(A - tanh Α)代替。但是，群体强化学习规则(10)由4个因素组成，这些因素来自4个不同的连续生物处理阶段：(i) 突触前活动，(ii) 突触后量，(iii) 具有对应动作的群体活动，以及(iv) 奖励。对于脉冲神经元，(7)和(10)的明确表达在"脉冲时序相关可塑性"学习规则中给出。
Online learning 为了获得在线学习规则，人们考虑了正在进行的刺激xt，例如定义脉冲序列取决于离散时间步骤 t。可以在每个时刻 t 采取动作At，尽管通常稀疏，但奖励信号Rt可能始终存在。为了表示每个时间步骤 t 的权重变化，我们考虑了所谓的突触资格迹et。在规则(9)的情况下，这被定义为瞬时可塑性诱导的低通滤波
，即et+1 = γet + PIt，且折扣因子为γ ∈ [0, 1)。在此，对数似然的导数如(10)所述，将各个因素低通滤波以得到完全在线规则。最终的规则变成：
通过低通滤波出现在(5), (7)和(8)中的相应瞬时可塑性诱导项PIt(与等式1中给出的Δw的一般形式相比)，人们可以类似地获得这些规则的在线版本。
假设状态xt是从部分可观察的马尔可夫决策过程(POMDP)采样的，则在线学习规则(11)可以显示为最大化期望折扣未来奖励：
对于每个时间步骤 t，一般情况请参见Baxter and Bartlett (2001)，定理5，以及Friedrich et al. (2011)，支持信息，用于群体学习。
Phenomenological R-STDP models 到目前为止讨论的基于梯度的学习规则通过确保平均可塑性诱导消失，<PI> = 0，阻止系统的权重漂移。这也假设在奖励调节的脉冲时序可塑性(R-STDP, Izhikevich (2007))。然而，当考虑有关可塑性诱导的具体(体外)数据时，通常在等式1中PI ≠ 0 (Sjöström and Gerstner, 2010)。因此，平均而言，奖励信号本身消失是合理的。实现此目标的一种策略是从调节因子中减去平均奖励，以使现在变为Δw = (R - <R>) · PI的学习规则再次无偏。这导致了actor批判学习的概念，其中特定于刺激的内部批判适应了可塑性诱导的全局调节信号，从而即使对于单个刺激也可以防止漂移。当STDP窗口中的LTD部分被抑制并且剩余的R-STDP被偏差校正时，标准关联任务的学习速度接近基于梯度的脉冲强化的学习速度(Frémaux et al., 2010)。
解决奖励偏差问题的一种很好的解决方案是，假设内部奖励信号是由一个时序核构成的，该时序核在整个时间内的总和为零，
，因此正的内部奖励信号必须跟随或先于一个否定的(Legenstein et al., 2008)。一种计算技巧似乎使人们想起了在果蝇中减轻疼痛的感觉(Tanimoto et al., 2004)，或啮齿动物的奖励基准适应(Schultz et al., 1997)。同样，配对奖励与差分Hebbian可塑性也被证明是无偏的，并且渐近等同于TD学习(Kolodziejski et al., 2009)。
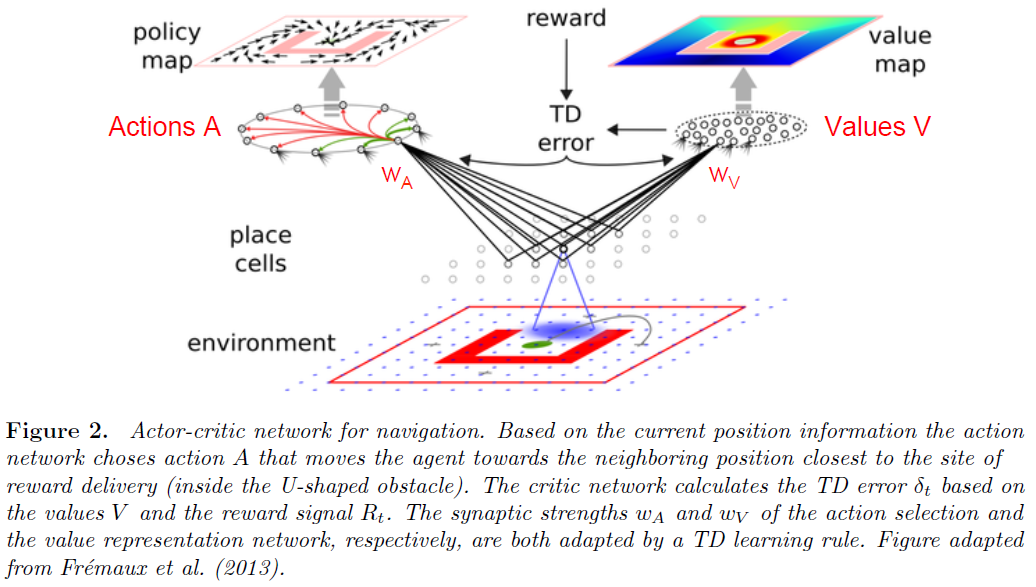
B) Temporal Difference (TD) learning TD方法代表一类学习规则，其中突触层次的调节反馈信号再次无偏。这些方法考虑了一个学习场景，在该场景中，智能体导航经过不同的状态最终达到终止奖励状态。
TD学习的actor-critic版本是为每个状态计算一个价值，并使用价值更新来训练动作选择网络(图2)。将状态x的价值定义为在时间 t 处于该状态时的期望折扣未来奖励(Sutton and Barto, 1998)，
其中γ表示折扣因子，并且根据固定策略π对所有未来动作都采用了期望<·>，参见Sutton and Barto (1998)。尽管此定义涉及未来奖励，但在线版本将再次需要仅根据过去的经验来估计量。因此，有趣的是，能够以递归方式将(13)重写为Vπ(xt) = <Rt> + γVπ(xt+1)。
假定价值函数Vπ(xt)由给定神经元的活动Vw(xt)表示(并近似)，其中w表示收敛到该神经元的突触强度，而xt是网络的输入。可以通过误差函数E = <V(x) - Vw(x)>2相对于w的梯度下降来在线调整突触强度，其中期望值超过状态x (Sutton and Barto, 1998; Frémaux et al., 2013)。因此，时间 t 的权重变化为：
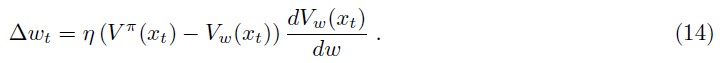
由于网络不知道真实价值V(xt)，因此可以使用Vπ(xt)的递归定义将其近似为Vπ(xt) ≈ R(t) + γVw(xt+1)。这导致学习规则：
其中δt被称为TD误差，由下式给出：
如果对价值Vw(x)进行编码的网络由单个神经元组成，比如说Vw(x) = Φ(u)，而u = wx，则突触学习规则可以表示为：
与上述策略梯度规则相比，通过将等式1中的奖励R(带有TD-δ)替换为TD学习规则(17)。由于在学习期间该δ值收敛到零，因此也可以抑制任何系统的权重漂移。
以actor-critic的形式进行的TD学习已经在SNN中得以实现(Castro et al., 2009; Potjans et al., 2009; Potjans et al., 2011; Frémaux et al., 2013)。在这些实现中，考虑了用于价值表征和动作选择的单独网络，并且两个网络中的突触强度w基于时序差分δt进行了调整(图2)。这种对actor-critic学习的替代方法是学习状态-动作对的价值("Q-值")，并根据这些价值选择动作("SARSA"，参见Sutton and Barto (1998))。但是，由于在标准神经元实现中对状态-动作对的价值进行评估需要实际选择该动作，因此无法以这种简单的形式来执行用于决定单独下一个动作的价值评估。
Policy gradient versus TD methods 在线策略梯度和TD学习两者均最大化由(12)和(13)表示的折扣未来奖励。但是，虽然策略梯度方法不需要网络上的特定结构或任务，但TD方法却需要。首先，TD学习假设状态x的内部表征。其次，TD误差的定义涉及两个后续状态，因此价值学习需要对所有相应的转换进行采样。第三，为一个状态分配价值时，隐含地假设达到那个状态的历史不会影响未来奖励。实际上，TD学习假设基础决策过程是马尔可夫模型。
基于梯度的学习不假定将价值分配给状态的内部表征。为了收敛，基于梯度的学习也不会假设基础决策过程的马尔可夫性。如果这种决策过程不为马尔可夫式，则TD学习可能会以两种方式失败，要么是在正确估计价值的同时选择不适当的动作，要么是错误地估计价值本身(Friedrich et al., 2011)。然而，当决策过程为马尔可夫式时，TD学习变得比策略梯度学习更快(Frémaux et al., 2013)。通过扩展状态空间表征并包括需要再次为其赋予价值的隐含状态，可以始终使决策过程成为马尔可夫式。然而，建模大脑如何创建这种隐含状态仍然是一个挑战(Dayan and Niv, 2008)。
Cortical implementations 由于其概念上的简单性，可以在参与刺激-响应关联并通过某些全局神经调节剂接收反馈的任何皮质网络中实现策略梯度方法。TD学习与基底神经节有关，在该神经节中，特定网络被认为代表价值(Daw et al., 2006; Wunderlich et al., 2012)，而多巴胺活动被认为代表TD误差δt (Schultz et al., 1997)。
尽管TD学习利用了有关基础模型的一些信息，但策略梯度和TD学习均被视为无模型的。如果包括更多信息(例如状态转换概率)，则学习可以再次变得更快，因为需要更少的采样来探索奖励函数。TD学习方法及其扩展已被证明在解释决策过程中的人类皮层活动方面是成功的(有关综述，请参见基于奖励的学习，基于模型的和无模型的)。