郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！
Neural Processing Letters, no. 1 (2015)
Abstract
在过去的几年中，在SNN领域进行的研究数量一直在稳定增长。对脉冲神经元建模，以近似生物神经元的复杂动态行为。它们通过离散脉冲进行通信，并用这些脉冲的时间对实际信息进行编码。正如Maass在有关第三代神经网络模型的论文中已经指出的那样，这使时间成为神经计算的中心因素。在本文中，我们在不同的粒度级别上研究了绝对时间和相对时间如何保证生物学启发的神经信息处理的新方法。在单个脉冲神经元的最低层次，我们概述了依赖于精确时间的神经脉冲的编码方案和学习技术。本文的第二部分提供了一个高层次的角度，重点是时间在网络层次上的作用。在这项工作中考虑的时间的第三方面和神经网络与实时系统的接口有关。在这种情况下，我们讨论了如何在计算机仿真和专门的神经形态硬件中实现按时间计算的概念。本文的贡献有两个方面：首先，我们展示了SNN中时间的精确建模如何作为基于神经生物学原理进行强大计算的重要基础。其次，通过介绍各种学习技术，我们证明了SNN在生物学上似乎对模式识别和路径规划等现实问题的适用性。
Keywords: Spiking Neural Network, Neurobiological Learning, Reservoir Computing, Hierarchical Learning, Neural Coding, Neuromorphic Hardware
1 Introduction
神经网络是AI和机器学习中最古老且应用最广泛的概念之一。它们的早期历史可以追溯到1950年左右，当时McCulloch和Pitts发表了他们著名的神经元模型[47]，而感知器是Rosenblatt构想的[59]。到那时，已经知道生物神经元通过离散脉冲(所谓的动作电位)进行通信。Hodgkin和Huxley在鱿鱼巨型轴突的开创性研究中得出了控制这些动作电位产生的神经动态的详细模型[27]。但是，由于计算神经状态更新涉及复杂的数学，即使在今天，这种模型也不是大规模仿真神经网络的可行方法。作为结果，研究人员开发了现象学近似法。在过去的几十年中，随着计算能力变得越来越便宜，这些近似值得到了进一步的完善和扩展。在[42]中，Maass确认了三个不同代的神经网络。第一代网络由McCulloch和Pitts引入的神经元组成，因此只能产生数字输出，这可以解释为存在或不存在脉冲。在第二代中，神经元的数字阈值逻辑被更通用的激活函数概念取代，该激活函数根据突触前传入神经提供的输入来计算连续输出。从生物学的角度来看，实值输出信号可以解释为脉冲发放率。通过证明第二代网络是通用函数近似，只要它们满足少量相对较弱的要求即可证实这一概念的计算能力[28]。
这两代神经网络在诸如光学字符识别，自然语言处理和机器人控制等各种应用中均取得了显著成果。最近，特别是深度神经网络和深度学习由于在监督分类任务中的空前性能而变得流行[63, 38]。但是，尽管早期ANN的主要动机是研究生物体中的神经信息处理，但大多数当前最新的神经结构和算法几乎与它们的生物学对应没有任何相似之处。这激发了第三代神经网络的发展，该网络捕获了生物体神经系统中存在的全部时间动态。与前几代不同，显式地对负责脉冲发放的内部过程进行建模，而不是仅基于简化的激活函数来计算抽象发放率。可用的神经元模型的范围从精确的定量生物学描述(如已经提到的Hodgkin-Huxley模型)到现象学近似(如LIF神经元[19]或Izhikevich神经元[29])。可以证明，独立于实际选择的模型，SNN在计算上比其前两代更强大[42]。更重要的是，它们一方面在机器学习，AI和机器人技术领域与另一方面在神经科学领域之间架起了一座桥梁。由于SNN不再从生物学过程中抽象出来，而是试图尽可能地重现它们，因此可以轻松地在不同学科之间交换新发现。欧盟资助的"人脑计划"[69]是专门设计用于通过将关于人脑的所有可用知识集成到大规模仿真中来促进这些协同效应的。结果旨在不仅促进神经科学，而且还促进基于神经信息处理原理的未来计算技术。
从生物学的角度来看，神经元传递信息的唯一方法是发出脉冲信号。但是，每个脉冲不携带任何数据。实验证据表明，实际的有效载荷因此必须在脉冲时间中编码[3]。这清楚地指出第一代和第二代神经元模型的主要缺点，这些模型仅通过指示脉冲是否已经发生或通过计算发放率而仅传达非常有限的时间信息。如实验中观察到的那样，只有SNN才能产生精确时间的脉冲，并能够实现依赖于后续脉冲的相对时间的学习的神经生物学机制。正如Maass所说，这开辟了"将时间用作计算和通信资源"的可能性[42]。
虽然SNN的生物学合理性和出色的计算能力已促使人们开发出多种基于脉冲的神经信息处理方法和技术，但对脉冲时间和通用时间作为一种计算手段进行详细回顾仍有缺失。在本文中，我们旨在通过从三个不同但连贯的角度研究时间的作用来填补这一空白。第2节重点介绍单个神经元，并概述了学习脉冲序列和相应应用的算法。在第3节中，我们说明了时间在网络层次上的作用，并说明了如何仔细调整相对时间可以产生更高层次的认知功能。当出于纯仿真的目的计算SNN的输出时，执行速度通常与结果无关。当网络连接到外部物理系统(例如实时且在现实世界中运行的机器人)时，这种情况就会改变。因此，第4节研究了神经仿真软件和新型神经形态硬件如何在适当的时间尺度上支持SNN的执行。在第5节中，我们通过概括本次回顾的主要结果来最后总结本文。
2 How Spiking Neurons Learn – The Role of Time at the Neural Level
在SNN中，每个神经元都是一个复杂的动态系统。与基于阈值逻辑或激活函数的神经模型不同，输出不仅取决于从其他神经元接收到的当前输入，而且取决于随时间变化的内部状态。这使脉冲神经元能够分别响应输入脉冲的不同时间序列。在下文中，我们将研究这些时间动态如何使单个神经元执行有意义的计算。第一小节简要介绍了对脉冲神经元进行数学建模的基础。此外，讨论了不同类型的神经编码方案，以演示如何基于脉冲的时间对信息进行编码。在第二小节中，我们回顾了专门为RL网络而设计的选定学习算法。通过提供一种方法来控制神经对输入脉冲模式的响应，这些算法使脉冲神经元能够执行诸如分类或特定输出模式生成之类的任务，从而可以按时间实现神经计算。
2.1 Biological and Mathematical Foundations
在将学习算法应用于脉冲神经元之前，必须先选择基础神经元模型并选择适当的神经代码。以下段落提供了所需的神经科学背景。
Mathematical Models for Spiking Neurons
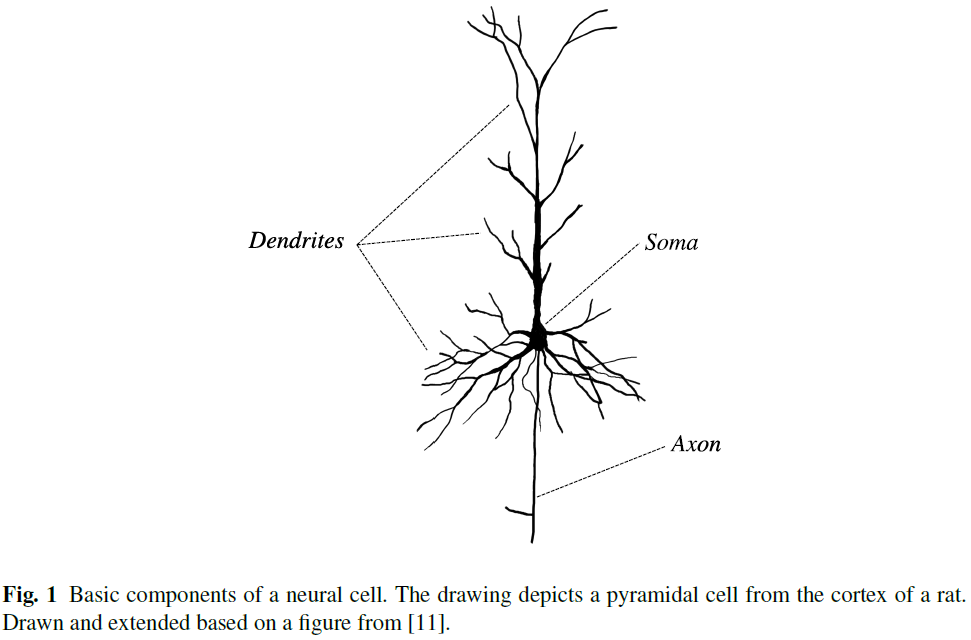
生物神经元具有分支的空间结构和内部状态，内部状态由化学过程决定。在图1中可以看到一个例子，它描绘了皮质锥体细胞的图。传入的脉冲沿着树突向胞体传播，并引起神经元膜电位的变化。一旦该电位超过阈值，就会产生一个脉冲并沿着轴突传播。轴突和其他神经元的树突之间的突触传递细胞之间的脉冲。在SNN中，通常通过假设每个神经元只是一个点来简化这种复杂的结构。而且，如前所述，基于电导的详细模型(如Hodgkin和Huxley得出的模型)通常被现象学近似所代替。这种类型的最简单，也是最常用的模型之一是LIF神经元，其特征在于以下等式[19]：
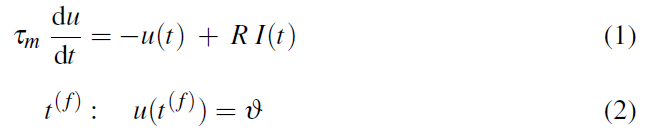
等式1对神经元的膜电位u进行建模，该神经元被认为是由电容器C和线性电阻R组成的电路。因素I(t)表示电流，由泄漏项和外部驱动输入电流组成。τm表示膜时间常数，对神经元的时间行为起决定性作用。脉冲发放由等式2描述，该等式2指出当膜电位从下方达到阈值
时，神经元在时间t(f)发放。请注意，并非所有脉冲神经元模型都基于微分方程。例如，Thorpe提出的模型仅计算所有传入脉冲的加权和，并假设每个神经元最多仅发放一个脉冲[62]。只有在重置神经元状态后才能生成新的脉冲。随机模型使用概率论中的工具描述神经动态，以允许引入噪声。
Neural Coding
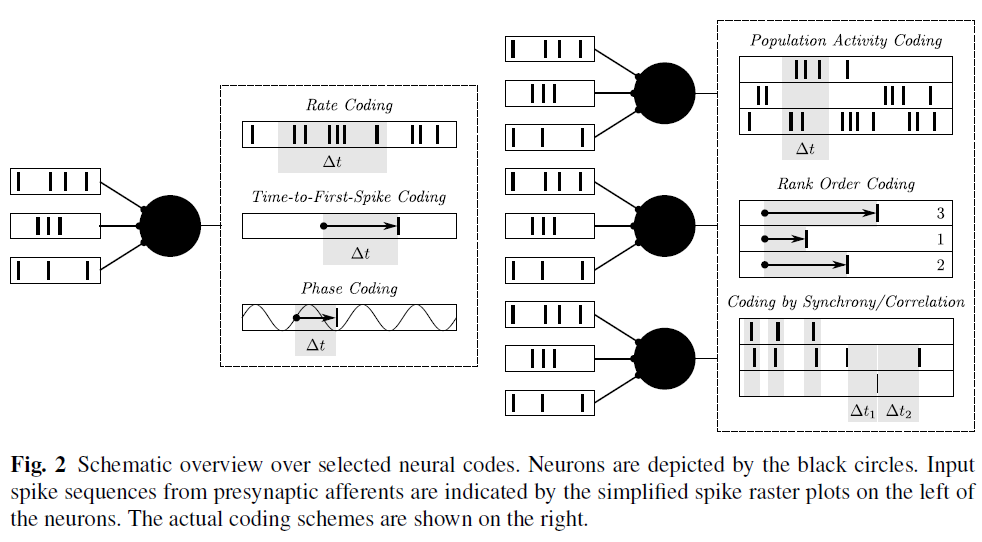
基于实验证据和理论考虑，已经构想出不同类型的潜在神经代码。然而，解密实际上在大脑中执行的神经代码的一般问题仍然是一个悬而未决的问题[19]。在下文中，我们将基于Gerstner et al. [19], Ponulak et al. [57] and Grüning et al. [22]的回顾提供常用编码方案的概述。这些回顾还提供了广泛的参考，以更详尽的信息层次讨论该问题，这超出了本文的范围。图2中的模式给出了下两段中显示的神经代码的图形摘要。
当仅考虑单个神经元时，发放率编码是编码带有脉冲的信息的最简单方法。如前所述，发放率代码不一定需要脉冲神经元模型，但也可以使用具有连续激活函数的第二代网络来实现。对于初次脉冲时间编码而言，情况并非如此，后者依赖于单个脉冲的精确时间。相对于某些刺激，所有信息仅在该脉冲的延迟时间中传递。相位编码是一种经过稍微修改的方法，其中相对时间的测量不是基于事件的开始，而是基于所考虑的神经系统中的周期性背景振荡。因此，在这种情况下的时间是指相移。在生物神经系统中已经观察到振荡行为，其形式是神经元群体发出的节律性脉冲模式。在单脉冲代码的某种程度退化的版本中，整个信息是由是否发生脉冲这一事实承载的[24]。脉冲发放时间被认为是无关紧要的。
如果涉及一个以上的神经元，以上给出的代码同样适用，但是针对神经元群体明确定义了其他编码方案。群体活动编码是神经群体的增强发放率编码。假设单个神经元从属于某个群体的所有神经元接收突触输入，则可以测量它们的整体活动，即在一定时间内发出脉冲的神经元的比例。像对单个神经元进行发放率编码一样，仅通过庞大的神经元总体活动编码信息似乎效率很低。因此，秩次编码考虑了选定的一组神经元的发放顺序。这种方法的缺点是，每个神经元最多只能考虑一个脉冲。基于同步或相关性的神经代码分别通过同步发放选定的神经元或通过其脉冲时间之间的精确定义的相关性对信息进行编码。最后，单个神经元或一组神经元发出的任何脉冲序列都可以视为神经编码。
2.2 Learning Techniques for Spiking Neurons
神经元模型和编码方案的特定组合为基于脉冲的神经信息处理定义了基本框架。但是，为了实现所需的行为或实现某些功能，需要设置其他参数。像在经典的ANN中一样，必须定义图状网络结构以指定神经元的数量及其连接性。网络内的信息流可以通过调整突触功效(即网络图中边的权重)和其他参数(如突触脉冲传输的延迟)来控制。正功效表明突触是兴奋性的，这意味着膜电位在脉冲到达时增加。负突触权重表示抑制性突触，其响应于传入动作电位而降低膜电位。注意，虽然模型突触很容易通过简单调整相应权重的符号在兴奋模式和抑制模式之间切换，但生物突触的属性取决于生理参数，因此不能在激发和抑制之间改变[34]。尽管已经提出了自动推导或调整神经网络拓扑的方法[13,72,52]，但研究的重点显然在于学习突触权重最优值的算法。图3说明了单个脉冲神经元的基本学习任务。基于传入的脉冲序列，所有用于脉冲神经元的学习算法的总体目标是调整突触功效，以使神经元产生所需的输出脉冲序列。在过去的几年中，机器学习和计算神经科学方面的研究产生了各种各样的不同学习技术，从专门为特定神经元模型设计的方法到仅依赖于所有脉冲神经元共有的基本特性的更通用的算法。另一个重要的分类标准是生物学合理性。它描述了学习算法的神经实现是否符合可从生物体中的神经系统获得的数据。接下来的段落概述了基于脉冲时间的神经生物学学习的最新技术。使用学习领域的常见概念，我们将区分非监督学习，强化学习和监督学习的方法。
Unsupervised Learning
Reinforcement Learning
由于没有办法指导学习过程朝着期望的目标发展，因此无监督学习的应用范围有所缩小。RL不仅通过提供输入数据，而且还提供对生成的输出的反馈进行编码的奖励信号来克服此限制。由于奖励是响应与外部系统的交互而动态传递的，因此RL特别适用于涉及与物理环境交互的机器人之类的应用。从神经学的角度来看，RL除了突触前和突触后的脉冲时间外，还为学习过程增加了第三个因素[15]。因此，一般而言，突触功效变化Δw可以表示如下(来自[64])：
在上式中，R表示收到的奖励，PI表示由突触前和突触后神经元发出的脉冲导致的可塑性诱导。选择PI的可能示例是图4中的STDP学习窗口。在神经层进行RL的主要挑战是确定当前奖励适用于哪些神经元和突触。与脉冲的持续时间或学习窗口的长度(以毫秒为单位)相比，奖励交付取决于环境，并且可能会延迟几秒钟。
奖励调节STDP (R-STDP)通过存储脉冲来解决此问题，如图6所示，这些脉冲可能是引发资格迹中突触变化的潜在候选。相关脉冲对由资格函数确定对迹的时序贡献。一旦接收到奖励信号，所有的突触权重都会通过计算奖励与相应突触资格迹的当前价值的乘积来更新。在[30]中，提出了生物学启发的R-STDP实现。每个突触都分配了一个额外的突触标签，该标签存储了资格迹信息，如果没有其他脉冲对出现，该标签会随时间衰减。与生物神经系统类似，奖励以神经调节剂多巴胺的形式发出。最终，将突触变化计算为突触标签的当前值与多巴胺浓度的乘积。基于统计模型的理论研究证明了R-STDP的计算能力，它使神经元能够学习分类任务和脉冲序列[40]。[12]中提供了一项根据实验结果更侧重于精确建模的研究。重要的是，作者指出了在只有单个全局奖励信号可用时，教导一组神经元以重现单个脉冲序列所涉及的问题。信度分配问题被完全忽略。取而代之的是，从理论上讨论了奖励预测的可能的生物学实现方式。
使神经生物学RL方法易于分析的一种常见方法是将其嵌入到机器学习领域的经典框架中。这允许基于策略梯度方法和TD学习对新的学习规则进行数学推导和分析。前一种算法通过计算估计期望奖励的函数的梯度来适应突触权重[64]。在[14]中，在局部可观察的马尔可夫决策过程中使用了一种用于RL的策略梯度算法，以得出针对脉冲神经元的RL规则。TD学习是一种更高级的方法，因为它不仅试图最大化下一个动作的奖励，而且还试图获得完整的未来期望奖励。与策略梯度方法一样，这需要一个近似函数。在运行期间，此函数会连续更新。在[15]中开发了这种所谓的critic的神经实现。作者将产生的学习规则介绍为TD-LTP，以强调突触可塑性受TD误差和突触长期增强的乘积调节。[64]中提供了进一步的RL算法的全面概述。
Supervised Learning
3 The Role of Timing at Network Level for Advanced Cognitive Capabilities
3.1 Reservoir Computing
3.2 Hierarchical Models of Learning and Cognition
4 Interfacing Neural Networks with Real-Time Applications
5 Conclusion & Outlook