郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！
论文笔记：https://zhuanlan.zhihu.com/p/55307499
Arxiv：https://arxiv.org/pdf/1802.09477.pdf
ICML 2018（TD3）
Abstract
在基于价值的RL方法(例如深度Q学习)中，已知函数近似误差会导致高价值估计和次优策略。我们表明，这个问题在actor-critic设置中仍然存在，并提出了新颖的机制以最小化它对actor和critic的影响。我们的算法建立在双重Q学习的基础上，通过采用一对critic之间的最小值来限制高估。我们得出了目标网络与高估偏差之间的联系，并提出延迟策略更新以减小每次更新误差并进一步提高性能。我们在OpenAI gym任务套件上评估了我们的方法，在每种测试环境中均优于最新技术。
1. Introduction
在具有离散动作空间的RL问题中，对因函数近似误差而导致的价值高估问题进行了深入研究。但是，在连续控制领域中，与actor-critic方法类似的问题在很大程度上未得到解决。在本文中，我们显示了高估偏差，并且时序差分方法中的累积误差存在于actor-critic设置中。我们提出的方法解决了这些问题，并且大大超过了现有技术。
高估偏差是Q学习的一种特性，其中带噪价值估计的最大化会引起一致的高估(Thrun＆Schwartz, 1993)。在函数近似设置中，考虑到估计器的不精确性，这种噪声是不可避免的。时序差分学习的本质进一步夸大了这种不准确性(Sutton, 1988)，其中使用后续状态的估计更新价值函数的估计。这意味着在每次更新中使用不精确的估计将导致误差累积。由于高估偏差，这种累积误差可能导致任意坏状态被估计为高价值，从而导致次优策略更新和发散的行为。
本文首先通过建立这种高估属性开始，该属性在连续控制设置中也存在于确定性策略梯度(Silver et al., 2014)。此外，我们发现离散动作设置下双重DQN中普遍存在的解决方案(Van Hasselt et al., 2016)在actor-critic设置中无效。在训练期间，双重DQN会使用单独的目标价值函数来估计当前策略的价值，从而可以在没有最大偏差的情况下评估动作。不幸的是，由于actor-critic设置下的策略变化缓慢，当前和目标价值估计仍然过于相似，无法避免最大化偏差。可以通过使用一对受过独立训练的critic，将较旧的双重Q学习(Van Hasselt, 2010)改编为actor-critic格式来解决。尽管这允许较少的有偏价值估计，但即使是具有高方差的无偏估计也可能导致未来在状态空间局部区域中的高估，进而可能对全局策略产生负面影响。为了解决这一问题，我们提出了一种截断的双重Q学习变体，该变体利用了这样一种观念，即遭受高估偏差的价值估计可以用作真实价值估计的近似上限。这有利于低估，在学习过程中往往不会传播，因为策略会避免采用低价值估计的动作。
考虑到噪声与高估偏差之间的联系，本文包含许多解决方差减少的组件。首先，我们表明目标网络是深度Q学习方法中的一种常见方法，它对于通过减少误差的累积来减少方差至关重要。其次，为了解决价值与策略的耦合问题，我们提出延迟策略更新，直到价值估计收敛为止。最后，我们介绍了一种新颖的正则化策略，其中SARSA样式的更新会引导相似的动作估计以进一步减少方差。
我们将这些修改应用于最先进的连续控制actor-critic方法(深度确定性策略梯度算法(DDPG)) (Lillicrap et al., 2015)，以形成双延迟深度确定性策略梯度算法(TD3) (一种actor-critic算法，它考虑了策略和价值更新中函数近似误差之间的相互影响。我们在来自OpenAI gym的七个连续控制域上评估了我们的算法(Brockman et al., 2016)，在这里我们的算法远远领先于现有技术。
鉴于最近对可复现性的关注(Henderson et al., 2017)，我们在大量随机种子上进行了实验，并采用了公平的评估指标，对每种贡献进行了消融研究，并开源了我们的代码和学习曲线(https://github.com/sfujim/TD3)。
2. Related Work
在先前的研究中，已经研究了RL算法中的函数近似误差及其对偏差与方差的影响(Pendrith et al., 1997; Mannor et al., 2007)。我们的工作着重于由于估计误差而产生的两个结果，即高估偏差和高方差累积。
存在一些方法来减少由于Q学习中的函数近似和策略优化而导致的高估偏差的影响。双重Q学习使用两个独立的估计器进行无偏价值估计(Van Hasselt, 2010; Van Hasselt et al., 2016)。其他方法直接关注于减少方差(Anschel et al., 2017)，最小化对早期高方差估计的过拟合(Fox et al., 2016)或通过校正项(Lee et al., 2013)。此外，已将价值估计的方差直接用于风险规避(Mannor＆Tsitsiklis, 2011)和探索(O'Donoghue et al., 2017)，但与高估偏差无关。
通过最小化每个时间步骤的误差大小或将异策回报与蒙特卡洛回报混合在一起，可以很大程度上解决因时序差分学习中的误差积累而引起的方差问题。我们的工作显示了减少每次更新误差的标准技术与目标网络的重要性，并开发了一种通过平均价值估计来减少方差的正则化技术。同时，Nachum et al. (2018)显示平滑价值函数可用于训练具有减少方差和改进性能的随机策略。具有多步回报的方法在累积估计偏差与策略和环境引起的方差之间进行权衡。通过重要性采样(Precup et al., 2001; Munos et al., 2016)，分布式方法(Mnih et al., 2016; Espeholt et al., 2018)以及近似界限(He et al., 2016)，这些方法已被证明是一种有效的方法。但是，这些方法未提供直接解决累积误差的方法，而是考虑了更长的视野，从而规避了该问题。另一种方法是降低折扣因子(Petrik＆Scherrer, 2009)，从而减少每个误差的影响。
我们的方法基于确定性策略梯度算法(DPG) (Silver et al., 2014)，这是一种actor-critic方法，它使用学到的价值估计来训练确定性策略。DPG扩展到深度RL，即DDPG(Lillicrap et al., 2015)，已显示出可以通过有效的迭代次数产生最先进的结果。与我们的方法正交的是，对DDPG的最新改进包括分布式方法(Popov et al., 2017)，以及多步回报和优先级经验回放(Schaul et al., 2016; Horgan et al., 2018)，以及分布式方法(Bellemare et al., 2017; Barth-Maron et al., 2018)。
3. Background
RL考虑了智能体与其环境交互的范例，旨在学习最大化奖励的行为。在每个离散时间步骤 t 处，给定状态为s ∈ S，智能体根据其策略π：S → A选择动作a ∈ A，收到奖励 r 和环境的新状态s'。回报被定义为奖励的折扣总和
，其中γ是确定短期奖励的优先级的折扣因子。
在RL中，目标是找到带有参数Φ的最优策略πΦ，该策略可使期望回报
最大化。对于连续控制，可以通过采用期望回报的梯度
来更新参数化策略πΦ。在actor-critic的方法中，可以通过确定性策略梯度算法(Silver et al., 2014)来更新称为actor的策略：
，在状态s及其后执行动作a时的期望回报称为critic或价值函数。
在Q学习中，可以使用时序差分学习(Sutton, 1988; Watkins, 1989)，一种基于Bellman方程的更新规则(Bellman, 1957)来学习价值函数。Bellman方程是状态-动作对(s, a)的价值与后续状态-动作对(s', a')之间的基本关系：
对于较大的状态空间，可以使用带有参数θ的可微函数近似Qθ(s, a)估算该值。在深度Q学习中(Mnih et al., 2015)，通过使用时序差分学习和二阶冻结目标网络Qθ'(s, a)来更新网络，以在多个更新中维持固定的目标y：
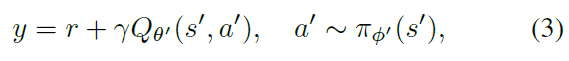
其中动作是由目标actor网络πΦ'中选择的。目标网络的权重要么定期更新以精确匹配当前网络的权重，要么在每个时间步骤上按一定比例τ进行更新θ' ← τθ + (1 - τ)θ'。可以以异策的方式应用此更新，从经验回放缓存中采样转换的随机小批处理(Lin, 1992)。
4. Overestimation Bias
在具有离散动作的Q学习中，使用贪婪的目标y = r + γ maxa' Q(s', a')更新价值估计，但是，如果目标对误差ε敏感，则超过该价值的最大值及其误差通常将大于真实最大值Eε[maxa' (Q(s', a') + ε)] ≥ maxa' Q(s', a') (Thrun＆Schwartz, 1993)。作为结果，即使是最初的零均值误差也可能导致价值更新导致一致的高估偏差，然后该偏差通过Bellman方程传播。这是有问题的，因为不可避免的是由函数近似引起的误差。
从分析最大化的角度来看，在离散动作设置中，高估偏差是显而易见的假象，而在通过规则下降来更新策略的actor-critic设置中，高估偏差的存在和影响尚不清楚。我们首先证明在第4.1节中的某些基本假设下，确定性策略梯度中的价值估计将被高估，然后在actor-critic设置中提出双重Q学习的截断变体，以减少第4.2节中的高估偏差。
4.1. Overestimation Bias in Actor-Critic
在actor-critic的方法中，会根据近似critic的价值估计来更新策略。在本节中，我们假定使用确定性策略梯度来更新策略，并显示该更新会导致价值估计中的过高估计。在给定当前策略参数Φ的情况下，让我们定义Φapprox为由近似critic Qθ(s, a)的最大化引起的actor更新的参数，并根据相对于真实基础价值函数Qπ(s, a)的假设actor更新来定义参数Φtrue(在学习过程中未知)：
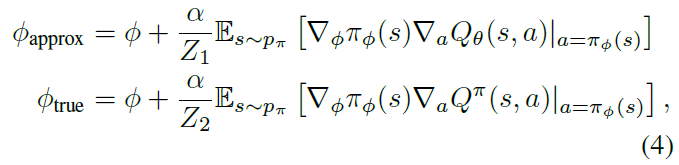
其中我们假设选择Z1和Z2来归一化梯度，即
。如果没有归一化梯度，则仍然可以保证在稍微严格的条件下仍会发生高估偏差。我们将在补充材料中进一步研究这种情况。我们分别将πapprox和πtrue表示为带有参数Φapprox和Φtrue的策略。
由于梯度方向是局部最大化器，因此存在足够小的ε1，以至于如果α ≤ ε1，则πapprox的近似价值将由πtrue的近似价值为下界：
相反，存在足够小的ε2，使得如果α ≤ ε2，那么πapprox的真实价值将由πtrue的真实价值为上界：
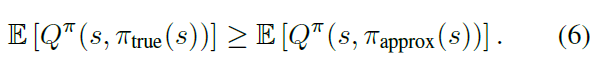
如果价值估计的期望至少与Φtrue的真实价值一样大，则E[Qθ(s, πtrue(s))] ≥ E[Qπ(s, πtrue(s))]，则等式(5)和(6)表示如果α < min(ε1, ε2)，则估计价值将被高估：
尽管每次更新时这种高估可能很小，但是误差的出现引起了两个问题。首先，如果任其发展，高估可能会在许多更新上形成更大的偏差。其次，不正确的价值估计可能会导致不良的策略更新。这特别有问题，因为创建了一个反馈循环，次优动作可能会由次优critic高度评价，从而在下一次策略更新中对其进行加强。
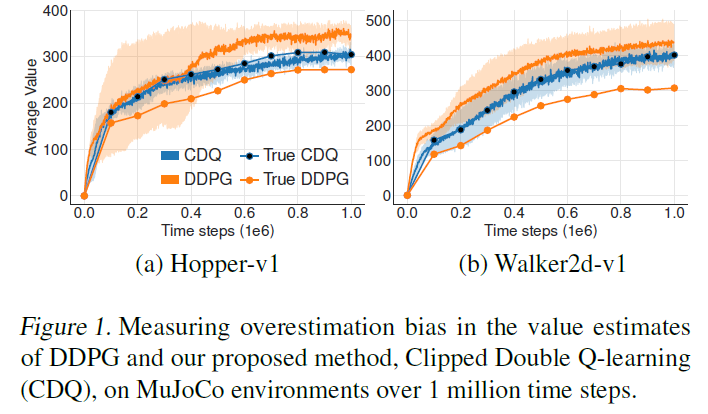
Does this theoretical overestimation occur in practice for state-of-the-art methods? 我们通过绘制在OpenAI gym环境Hopper-v1和Walker2d-v1上(Brockman et al., 2016)学习时随时间变化的DDPG的价值估计(Lillicrap et al., 2015)来回答这个问题。在图1中，我们绘制了10000个状态的平均价值估计，并将其与真实价值估计进行比较。真实价值是根据当前策略之后从1000个回合中的平均折扣回报(从回报缓存采样的状态开始)估计得出的。学习过程中会出现非常明显的高估偏差，这与我们在下一节中介绍的新颖方法(截断的双重Q学习)相反，后者大大减少了critic的高估。
4.2. Clipped Double Q-Learning for Actor-Critic
虽然已经提出了几种减少高估偏差的方法，但我们发现它们在actor-critic设置中无效。本节介绍了一种新颖的双重Q学习的截断变体(Van Hasselt, 2010)，该变体可以用任何actor-critic方法代替critic。
在双重Q学习中，通过保持两个单独的价值估计，使贪婪更新与价值函数脱离纠缠，每个价值估计用于更新另一个价值估计。如果价值估计是独立的，则可以使用它们对使用相反的价值估计选择动作进行无偏估计。在双重DQN中(Van Hasselt et al., 2016)，作者提出使用目标网络作为价值估计之一，并通过贪婪最大化当前价值网络而不是目标网络来获得策略。在actor-critic设置中，类似的更新使用当前策略而不是学习目标中的目标策略：
但是实际上，我们发现，由于actor-critic策略的变化缓慢，当前网络和目标网络过于相似，以至于无法进行独立估计，并且几乎没有改进。取而代之的是，可以使用原始的双重Q学习公式，由一对actor (πΦ1, πΦ2)和critic (Qθ1, Qθ2)组成，其中πΦ1是相对于Qθ1优化的，πΦ2是相对于Qθ2优化的：
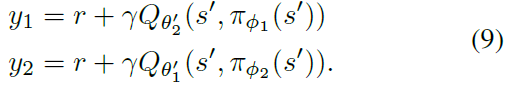
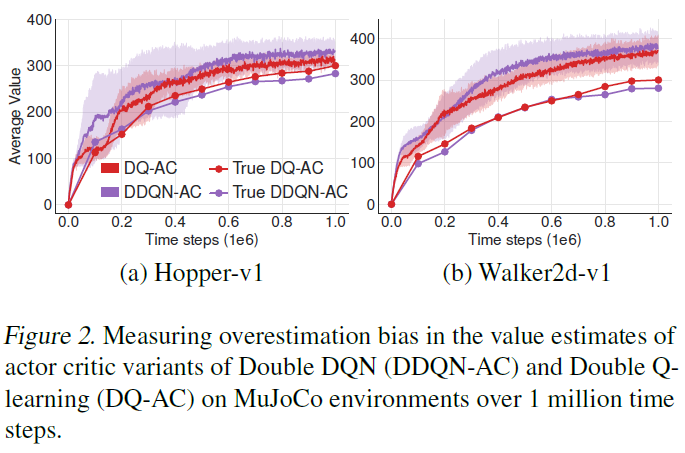
我们在图2中测量了高估偏差，该偏差表明actor-critic双重DQN遭受了与DDPG类似的高估(如图1所示)。尽管双重Q学习更有效，但它并不能完全消除高估。我们在6.1节中进一步表明，这种减少在实验上是不够的。
当πΦ1相对于Qθ1优化时，在Qθ1的目标更新中使用独立的估计将避免策略更新引入的偏差。但是，由于在学习目标中使用了相反的critic以及相同的回放缓存，因此critic并不是完全独立的。作为结果，对于某些状态s，我们将得到
。这是有问题的，因为
通常会高估真实价值，并且在状态空间的某些区域中，高估会进一步被夸大。为了解决这个问题，我们建议将偏差较小的价值估计Qθ2简单地乘以有偏估计Qθ1的上限。这导致取两个价值估计之间的最小值，以给出截断的双重Q学习算法的目标更新：
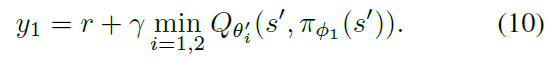
使用截断的双重Q学习，与使用标准Q学习目标相比，价值目标无法引入任何额外高估。尽管此更新规则可能会导致低估偏差，但它比高估偏差更可取，因为与高估动作不同，低估动作的价值不会通过策略更新显式传播。
在实现中，可以通过使用针对Qθ1优化的单个actor来降低计算成本。然后，我们对Qθ2使用相同的目标y2 = y1。如果Qθ2 > Qθ1，则更新与标准更新相同，并且不会引起额外偏差。如果Qθ2 < Qθ1，则表明发生了高估，并且使用类似于双重Q学习的方法可以降低该价值。从这种直觉可以得出有限MDP设置下的收敛证明。我们在补充材料中提供正式的细节和理由。
第二个好处是，通过将函数近似误差视为随机变量，我们可以看到，最小值运算符应为方差估计误差较小的状态提供更高的价值，因为一组随机变量的期望最小值随着随机变量方差的增加而减小。这种影响意味着等式(10)中的最小化将导致偏向于具有低方差价值估计的状态，从而导致具有稳定学习目标的更安全的策略更新。
5. Addressing Variance
尽管第4节讨论了方差对高估偏差的贡献，但我们也认为方差本身应直接解决。除了对高估偏差的影响外，高方差估计还会为策略更新提供带噪梯度。众所周知，这会降低学习速度(Sutton＆Barto, 1998)，并在实践中损害性能。在本节中，我们强调最小化每次更新时的误差，建立目标网络与估计误差之间的联系以及对actor-critic的学习过程进行修改以减少方差的重要性。
5.1. Accumulating Error
由于时序差分更新，其中根据后续状态的估计来构建价值函数的估计，因此会产生误差。尽管可以合理地期望单个更新的误差很小，但是这些估计误差可能会累积，从而可能导致较大的高估偏差和次优的策略更新。在函数近似设置中，Bellman方程从未得到完全满足，并且每次更新都会留下一些残留的TD误差δ(s, a)：
然后可以证明，价值估计不是学习期望回报的估计，而是估计期望回报减去未来TD误差的期望折扣总和：
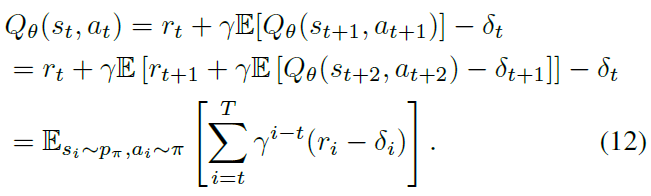
如果价值估计是未来奖励和估计误差的函数，则可以得出估计的方差与未来奖励和估计误差的方差成正比。给定较大的折扣因子γ，如果不克服每次更新的误差，则每次更新的方差都会迅速增加。此外，每个梯度更新仅相对于小型迷你批次减少了误差，这不能保证迷你批次外部的价值估计中的误差大小。
5.2. Target Networks and Delayed Policy Updates
在本节中，我们检查目标网络与函数近似误差之间的关系，并显示使用稳定的目标可减少误差的增长。在设计RL算法时，这种见解使我们能够考虑高方差估计与策略性能之间的相互作用。
目标网络是在深度RL中实现稳定性的众所周知的工具。由于深度函数近似需要多个梯度更新来收敛，因此目标网络在学习过程中提供了稳定的目标，并允许更大范围地覆盖训练数据。如果没有固定的目标，则每次更新都可能会留下残留误差，该误差将开始累积。尽管误差的累积本身可能是有害的，但与最大化价值估计的策略配合使用时，可能会导致价值大相径庭。
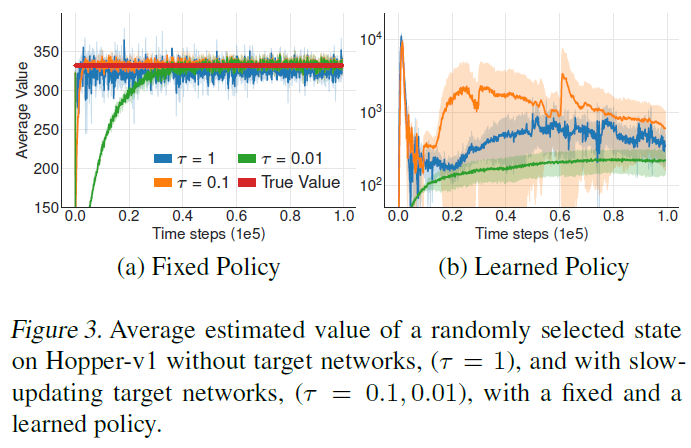
为了提供一些直觉，我们在图3中的critic和actor上检查了有目标网络和没有目标网络的学习行为，其中我们以与图1类似的方式在Hopper-v1环境中绘制了价值。在(a)中，我们将行为与固定策略进行比较；在(b)中，我们使用持续学习的策略检查价值估计，并使用当前价值估计进行训练。目标网络使用缓慢移动的更新速率τ。
尽管在没有目标网络(τ = 1)的情况下更新价值估计会增加波动性，但考虑固定策略时，所有更新速率都会导致类似的收敛行为。但是，当使用当前价值估计训练策略时，使用快速更新的目标网络会导致行为大相径庭。
When do actor-critic methods fail to learn? 这些结果表明，在没有目标网络的情况下发生的差异是策略更新的结果，该策略更新具有较高的方差价值估计。图3和第4节表明，失败可能是由于actor与critic更新之间的相互作用而发生的。当策略较差时，价值估计会因高估而发生分歧，如果价值估计本身不准确，则策略将变得糟糕。
如果可以使用目标网络来减少多次更新中的误差，并且高误差状态下的策略更新会导致不同的行为，则应该以比价值网络更低的频率更新策略网络，以在引入策略更新之前首先最小化误差。我们提出延迟策略更新，直到价值误差尽可能小为止。修改是仅在对critic进行固定数量的更新后更新策略和目标网络。为了确保TD误差保持较小，我们缓慢地更新目标网络
。
通过充分延迟策略更新，我们限制了针对未更改的critic重复更新的可能性。确实发生的低频策略更新将使用方差较小的价值估计，并且原则上应导致质量更高的策略更新。这创建了两个时间尺度的算法，这通常是线性设置中收敛所需的(Konda & Tsitsiklis, 2003)。我们的经验结果在6.1节中显示了此策略的有效性，该结果显示了性能的提高，同时使用了较少的策略更新。
5.3. Target Policy Smoothing Regularization
确定性策略的一个问题是，它们可能过拟合于价值估计中的狭窄峰值。在更新critic时，使用确定性策略的学习目标极易受到函数近似误差引起的不准确的影响，从而增加了目标的方差。可以通过正则化减少这种产生的方差。我们引入了用于深度价值学习的正则化策略，目标策略平滑，它模仿了SARSA的学习更新(Sutton＆Barto, 1998)。我们的方法强化了这样的观念，即相似的动作应该具有相似的价值。虽然函数近似会隐式执行此操作，但是可以通过修改训练过程来显式强制相似动作之间的关系。我们提出对目标动作周围的一小部分区域进行拟合：
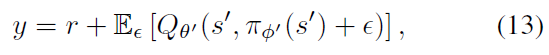
通过自举类似的状态-动作价值估计，可以使价值估计变得平滑。在实践中，我们可以通过向目标策略中添加少量随机噪声并平均迷你批次来近似对动作的期望。这使我们修改了目标：
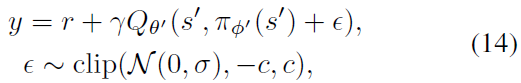
其中截断增加的噪音以使目标接近原始动作。结果是一种让人联想到Expected SASAR的算法(Van Seijen et al., 2009)，其中价值估计是异策学习的，并且独立于探索策略选择添加到目标策略中的噪声。学到的价值估计与参数σ定义的带噪策略有关。
凭直觉，众所周知，从SARSA价值估计得出的策略往往更安全，因为它们为抵抗干扰的动作提供了更高的价值。因此，这种更新方式可以额外导致出现故障情况的随机域的改进。Nachum et al. (2018)同时提出了类似的想法，对Qθ而不是Qθ'进行平滑处理。
6. Experiments
我们介绍了双重延迟深度确定性策略梯度算法(TD3)，该算法基于深度确定性策略梯度算法(DDPG) (Lillicrap et al., 2015)，通过应用第4.2、5.2和5.3节中所述的修改来增加稳定性和性能，并考虑了函数近似误差。TD3拥有一对critic和一个actor。对于每个时间步骤，我们将一对critic更新为目标策略选择的动作的最小目标价值：
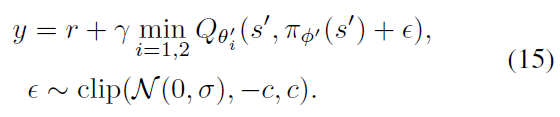
每进行d次迭代，遵循确定性策略梯度算法(Silver et al., 2014)就Qθ1更新策略。TD3在算法1中进行了总结。
6.1. Evaluation
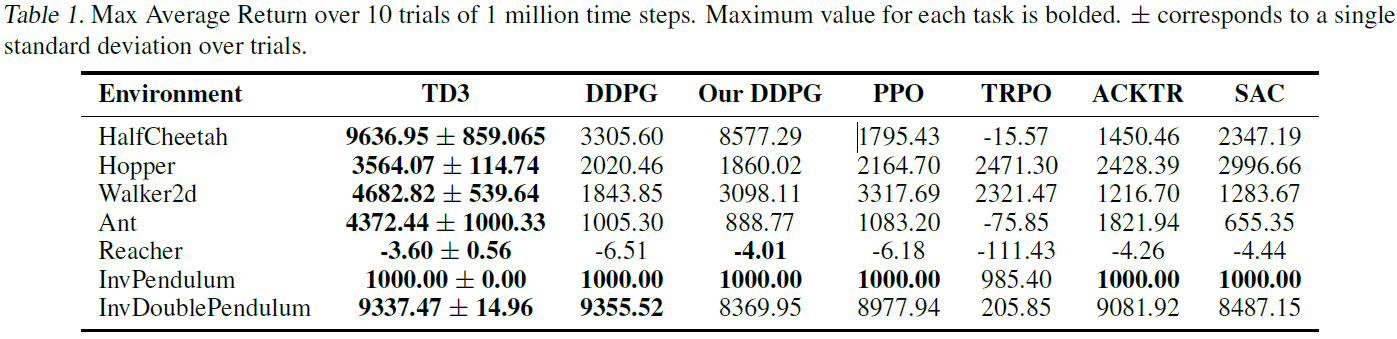
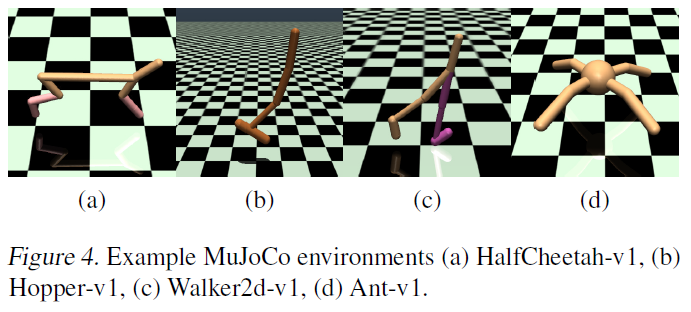
为了评估我们的算法，我们在通过OpenAI Gym进行交互的MuJoCo连续控制任务套件(Todorov et al., 2012)上衡量其性能(Brockman et al., 2016) (图4)。为了进行可重复的比较，我们使用Brockman et al. (2016)的原始任务集，且未对环境或奖励进行任何修改。
对于DDPG的实现(Lillicrap et al., 2015)，我们使用分别由400个隐含节点和300个隐含节点组成的两层前馈神经网络，在每一层之间针对actor和critic均具有ReLU，最后tanh单元跟随actor的输出。与原始DDPG不同，critic将状态和动作都作为第一层的输入。两个网络参数都使用Adam (Kingma＆Ba, 2014)进行更新，学习率为10-3。在每个时间步骤之后，都使用100个转换的小批量来训练网络，这些转换是从包含智能体完整历史的回放缓存中均匀采样的。
通过将ε ～ N(0, 0.2)添加到目标actor网络选择的动作中来实现目标策略平滑(裁剪为(-0.5, 0.5)，延迟策略更新包括每d次迭代(d = 2)仅更新actor和目标critic网络。虽然较大的d会在累积误差方面带来更大的好处，但为了公平比较，critic每个时间步骤仅训练一次，而对actor训练的迭代太少会削弱学习。这两个目标网络都以τ = 0.005进行更新。
为了消除对策略初始参数的依赖，我们对稳定长度环境的前10000个时间步骤(HalfCheetah-v1和Ant-v1)和其余环境的前1000个时间步骤使用纯探索性策略。然后，我们使用异策探索策略，将高斯噪声N(0, 0.1)添加到每个动作中。与DDPG的原始实现方式不同，我们使用不相关的噪声进行探索，因为我们发现从Ornstein-Uhlenbeck (Uhlenbeck＆Ornstein, 1930)过程中提取的噪声没有提供性能提升。
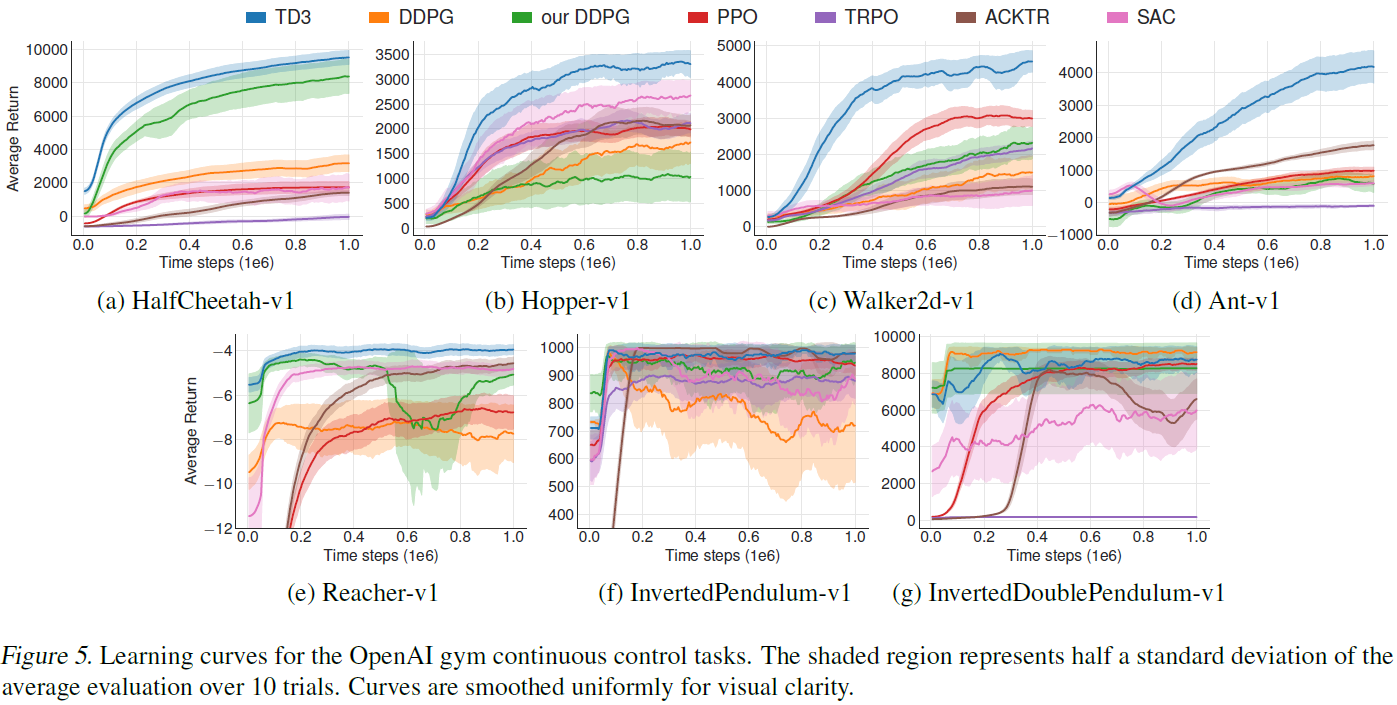
每个任务运行一百万个时间步骤，每5000个时间步骤进行一次评估，其中每个评估报告10个回合的平均奖励(不带探索噪声)。我们的结果报告了Gym模拟器和网络初始化上的10个随机种子。
我们将算法与DDPG (Lillicrap et al., 2015)以及最新的策略梯度算法进行了比较：PPO (Schulman et al., 2017)，ACKTR (Wu et al., 2017)和TRPO (Schulman et al., 2015) (由OpenAI的基准存储库(Dhariwal et al., 2017)实现，以及SAC (Haarnoja et al., 2018)，由作者的GitHub1实现。此外，我们将我们的方法与DDPG的重新调整版本进行了比较，该版本包括DDPG的所有结构和超参数修改，而没有任何我们提出的调整。补充材料中提供了我们重新调整的版本与基准DDPG之间的完整比较。
我们的结果显示在表1中，学习曲线显示在图5中。TD3在所有任务的最终性能和学习速度上均达到或优于其他所有算法。
1请参见有关超参数的补充材料，以及关于SAC报告结果中差异的讨论。
6.2. Ablation Studies
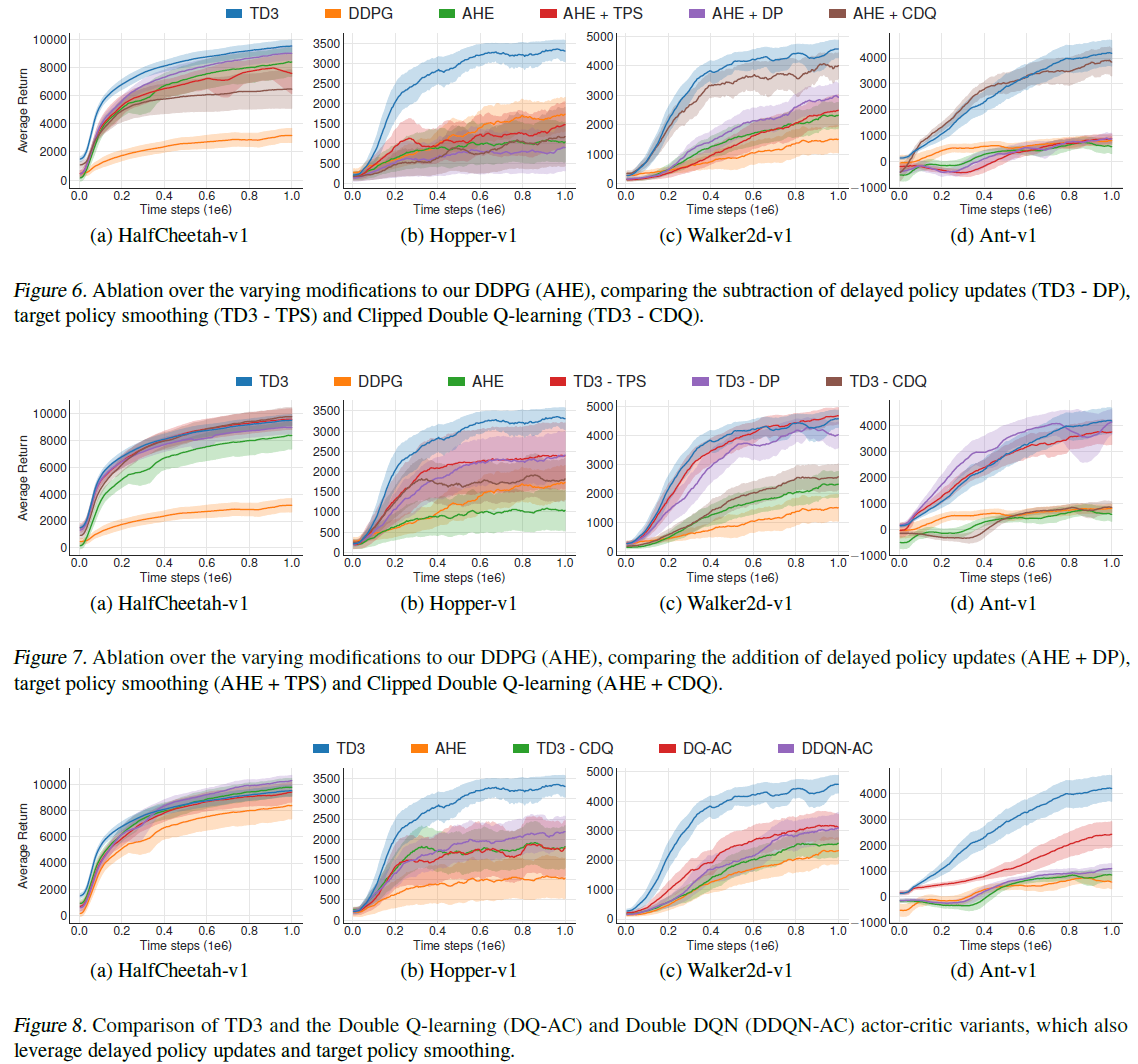
我们进行消融研究，以了解每个单独组件的作用：截断的双重Q学习(第4.2节)，延迟策略更新(第5.2节)和目标策略平滑(第5.3节)。我们在表2中给出了结果，其中我们比较了从TD3删除每个组件的性能以及对结构和超参数的修改。在补充材料中可以找到其他学习曲线。
每个组件的重要性因任务而异。尽管在大多数情况下仅添加单个组件不会带来明显的改进，但添加组合的效果却更高。在大多数任务中，完整算法的性能优于其他所有组合。尽管仅对actor进行了一半迭代次数的训练，但包含延迟策略更新通常可以提高性能，同时减少训练时间。
我们还比较了表2中分别表示为DQ-AC和DDQN-AC的双重Q学习(Van Hasselt, 2010)和双重DQN(Van Hasselt et al., 2016)的actor-critic变体的有效性。相比较而言，这些方法还受益于延迟策略更新，目标策略平滑以及使用我们的结构和超参数。这两种方法都比第4节中的截断的双重Q学习减少了高估偏差。这在经验上得到了反映，因为这两种方法均导致对TD3-CDQ的改进不明显，但在Ant-v1环境中例外，这似乎可以从任何高估减少中受益匪浅。由于在我们的完整方法中包含截断的双重Q学习的效果优于之前的两种方法，这表明服从无偏估计器的高估是提高性能的有效措施。
7. Conclusion
高估已被确定为基于价值的方法中的关键问题。在本文中，我们建立了高估偏差在actor-critic方法中也是有问题的。我们发现，在actor-critic设置下，通过离散动作来减少深度Q学习中的高估偏差的通用解决方案是无效的，并开发了双重Q学习的新型变体，它限制了可能的高估。我们的结果表明，减轻高估可以大大提高现代算法的性能。
由于噪声和高估之间的联系，我们研究了时序差分学习中误差的累积。我们的工作调查了深度RL中的标准技术(目标网络)的重要性，并研究了它们在限制因不精确函数近似和随机优化而产生的误差中的作用。最后，我们介绍了一种SARSA样式的正则化技术，该技术修改了时序差分目标以引导出类似的状态-动作对。
总而言之，这些改进定义了我们提出的方法，即双重延迟深度确定性策略梯度算法(TD3)，该方法极大地提高了DDPG在连续控制设置下许多挑战性任务中的学习速度和性能。我们的算法超越了众多先进算法的性能。由于我们的修改易于实现，因此可以轻松将其添加到任何其他actor-critic算法中。
Supplementary Material
A. Proof of Convergence of Clipped Double Q-Learning
B. Overestimation Bias in Deterministic Policy Gradients
C. DDPG Network and Hyper-parameter Comparison
D. Additional Implementation Details
E. Soft Actor-Critic Implementation Details
F. Additional Learning Curves
