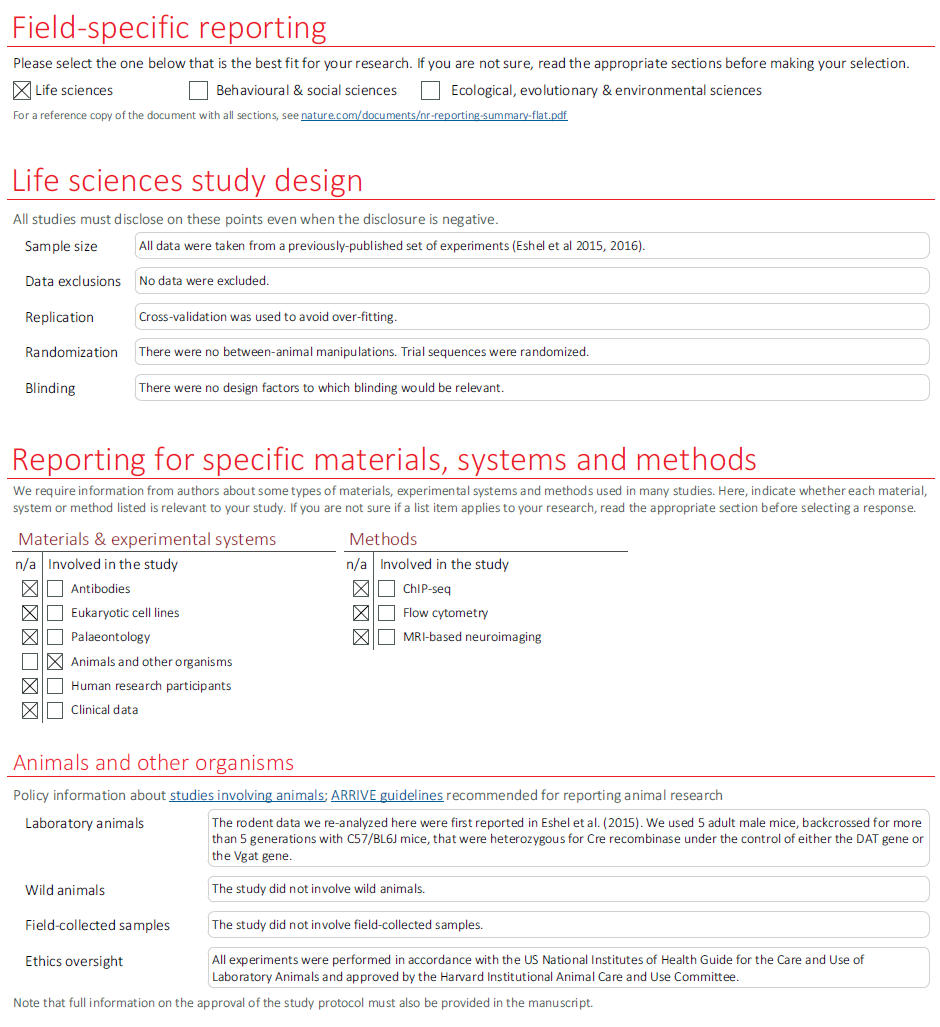
郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！
Nature 2020
汇报PPT：
链接：https://pan.baidu.com/s/1RWx6miX6iZUNgNfV9B69FQ
提取码：x5cz
基础概念：
分位数：https://www.zhihu.com/question/67763556
线性回归检验：https://www.cnblogs.com/tinglele527/p/12015449.html
https://www.zhihu.com/question/30753175
https://www.zhihu.com/question/23149768/answer/282842210
- t检验：t检验是对单个变量系数的显著性检验，一般看P值；如果P值小于0.05表示该自变量对因变量解释性很强。
- F检验：F检验是对整体回归方程显著性的检验，即所有变量对被解释变量的显著性检验。
Abstract
自推出以来，多巴胺的奖励预测误差理论已经解释了许多经验现象，为理解大脑中奖励和价值的表示提供了统一的框架1-3。根据现在的规范理论，奖励预测表示为单个标量，它支持学习随机结果的期望价值或均值。在这里，我们提出了一种基于多巴胺的强化学习方法，该方法受最近关于分布强化学习的人工智能研究的启发4-6。我们假设大脑不是以均值的方式，而是以概率分布的方式来代表未来可能的奖励，可以有效地并行表示多个未来结果。这个想法意味着一组经验预测，我们使用来自小鼠腹侧被盖区的单电极记录对其进行了测试。我们的发现为神经网络实现分布强化学习提供了有力的证据。
多巴胺的奖励预测误差（RPE）理论源自人工智能（AI）领域中强化学习（RL）的工作7。自从与神经科学的联系首次建立以来，RL就取得了长足的进步8,9，揭示了极大提高RL算法有效性的因素10。在某些情况下，相关的机制要求与神经功能进行比较，从而提出有关大脑中基于奖励的学习的假设11-13。在这里，我们研究了AI研究中有希望的最新进展，并研究了其潜在的神经相关性。具体来说，我们考虑一个被称为分布强化学习4-6的计算框架（图1a,b）。
与多巴胺理论所基于的传统形式的时序差分RL相似，分布RL假设基于奖励的学习是由RPE驱动的，这表明了所获得的奖励与预期奖励之差。（为简单起见，我们从单步转移模型的角度介绍了该理论，但是对于一般的多步（折扣奖励）情况，该原理仍然适用；请参见补充信息。）分布RL的主要区别在于“ 预期奖励”如何被定义。在传统RL中，奖励预测被表示为单个数：所有未来奖励结果的均值，并按其各自的概率加权。相比之下，分布RL使用多种预测。这些预测对即时奖励的乐观程度各不相同。更乐观的预测预期会获得更大的未来奖励；预测越不乐观，预期的结果就越少。整个预测范围将捕获未来奖励的全部概率分布（补充信息中有更多详细信息）。
与传统的RL程序相比，分布RL可以将深度学习系统的性能提高两倍或更多5,14,15，这种效应部分源于对表征学习的增强（请参见扩展数据图2, 3和补充信息）。这暗示了问题：大脑中的RL是否可能利用分布编码的好处。大脑利用许多其他领域中的分布编码16这一事实，以及分布RL的机制在生物学上是合理的6,17，都鼓舞了这个问题。在这里，我们使用执行带有概率奖励任务的小鼠腹侧被盖区（VTA）中的单电极记录测试了分布RL的几种预测。
图1 | 分布价值编码源于正负预测误差的相对缩放比例的多样性。
a，在多巴胺系统的标准时序差分（TD）理论中，所有价值预测器都学习相同的价值V。假定每个多巴胺细胞对于正与负的RPE都具有相同的相对缩放比例（左）。这将使每个价值预测（或价值基准）成为结果分布的均值（中间）。虚线表示零RPE或刺激前发放。
b，在我们提出的分布TD模型中，对于正（α+）和负（α-）的RPE，不同的通道具有不同的相对缩放比例。红色阴影表示α+>α-，蓝色阴影表示α->α+。α+和α-之间的不平衡会导致每个通道学习不同的价值预测。这组价值预测共同代表了可能的奖励分布。
c，我们分析了两个任务的数据。在可变幅度的任务中，只有一个信号，然后是幅度不可预测的奖励。
d，在可变概率任务中，存在三个信号，每个信号表示不同的奖励概率，并且奖励幅度是固定的。
Value predictions vary among dopamine neurons
与经典时序差分（TD）学习相反，分布RL设置了一组不同的RPE通道，每个通道都具有不同的价值预测，并且各个通道的乐观程度不同。（在RL中将价值正式定义为未来结果的均值，但在此我们放宽此定义，以包括不一定是均值的未来结果预测。）这些价值预测又为不同的RPE信号提供了参考点，从而导致后者在乐观方面也有所不同。令人惊讶的结果是，单个奖励结果可以同时引发正的RPE（在相对悲观的通道内）和负的RPE（在较乐观的通道内）。
这立即转化为神经科学的预测，即多巴胺神经元应该在“乐观”中表现出这种多样性。假设一个智能体已经了解到信号可以预测奖励，其幅度将取决于概率分布。在标准RL理论中，获得幅度低于此分布均值的奖励将引起负的RPE，而幅度高于此分布均值的奖励将引起正的RPE。标准RL中的反转点（预测误差的幅度从负到正）是对幅度分布的期望。相比之下，在分布RL中，根据多巴胺神经元的乐观程度，其反转点有所不同。
我们在光遗传学验证的多巴胺能VTA神经元中测试了这种反转点多样性，重点是对收到的液体奖励的响应，该奖励量是在每个试验中从七个可能的值中随机抽取的（图1c）。正如分布RL（而不是标准RL理论）所预期的，我们发现多巴胺神经元具有明显不同的反转点，范围从在最小的两个奖励之间反转的细胞到在最大的两个奖励之间反转的细胞（图2a,b）。这种多样性不是由噪声引起的，因为根据随机取的一半数据估计的反转点是针对根据另一半数据估计的反转点的鲁棒预测器（线性回归中R=0.58，P=1.8×10-5；图2c）。实际上，对于5μl奖励的响应，在40个细胞中，有13个细胞明显高于基准，并且有10个细胞明显低于基准。请注意，虽然有些细胞表现为悲观而另一些表现为乐观，但也有一群细胞具有大致中性的响应，这是由分布RL模型预测的（与图2a右侧比较）。
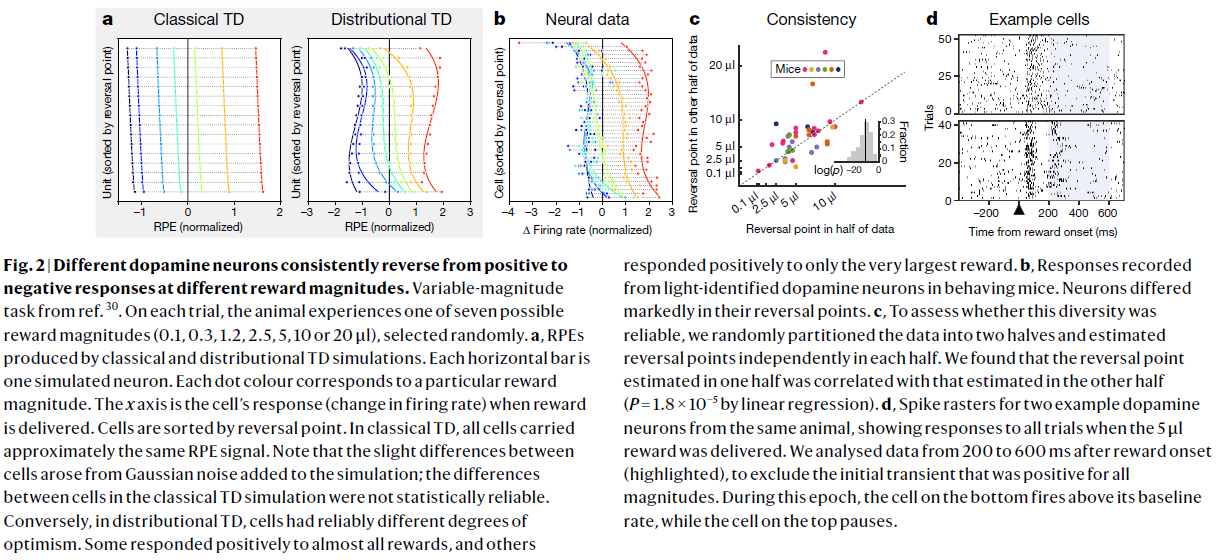
图2 | 不同的多巴胺神经元始终以不同的奖励幅度从正响应变为负响应。
参考文献30的可变幅度任务。在每次试验中，动物都会经历随机选择的七个可能的奖励量之一（0.1, 0.3, 1.2, 2.5, 5, 10或20μl）。
a，由经典和分布TD仿真产生的RPE。每个水平条都是一个模拟的神经元。每个点的颜色对应于特定的奖励幅度。x轴是提供奖励时细胞的响应（发放率的变化）。细胞按反转点排序。在经典TD中，所有细胞都携带大致相同的RPE信号。请注意，细胞之间的细微差异是由添加到模拟中的高斯噪声引起的。经典TD模拟中细胞之间的差异在统计上不可靠。相反，在分布TD中，细胞具有可靠的不同乐观程度。一些细胞对几乎所有奖励都做出正响应，但也有细胞仅对最大奖励做出正响应。
b，行为小鼠的光识别多巴胺神经元记录的响应。神经元的反转点明显不同。
c，为了评估这种多样性是否可靠，我们将数据随机分为两半，并在每一半中独立估计反转点。我们发现，在一半中估计的反转点与在另一半中估计的反转点相关（通过线性回归，P=1.8×10-5）。
d，来自同一只动物的两个示例多巴胺神经元的脉冲栅格，显示在提供5μl奖励时对所有试验的响应。我们分析了奖励发生后200-600ms（突出显示）后的数据，以排除所有幅度均为正的初始瞬变。在此时期内，底部的细胞发放率在基准以上，而顶部的细胞会暂停发放。
对我们理论的更强有力的检验是这种多样性是否也存在于单个动物中。大多数动物的分析细胞太少，但是在记录细胞数最多的单只动物中，一半数据估计的反转点可以强有力地预测另一半数据所估计的反转点（P=0.008）。此外，以响应单个奖励幅度（5μl），16个细胞中有6个细胞明显高于基准，而16个细胞中有5个细胞明显低于基准。最后，图2d显示了来自该动物的两个示例细胞的栅格，它们对同一奖励表现出始终相反的响应。
由于我们观察到的多样性在所有试验中都是可靠的，因此无法通过在非分布TD模型中添加测量噪声来解释。如补充信息第2节中所述（另请参见扩展数据图4），我们还分析了一些更精细的替代模型，尽管其中某些模型在某些分析方法下会引起反转点多样性的出现， 相同的模型与实验数据的其他方面矛盾，我们将在下文进行汇报。
我们的第一个预测是关于多巴胺能信号和奖励幅度之间的关系。多巴胺能RPE信号也根据奖励概率进行缩放2,18，而分布RL也导致该域的预测。为此，我们分析了第二项任务的数据，其中感官信号表明了即时液体奖励的可能性（图1d）。三个信号分别表示奖励的概率为10％，50％和90％。标准RPE理论预测，考虑到信号出现时的响应，所有多巴胺神经元在10％，50％和90％信号响应之间应具有相同的相对间隔。（在中性风险偏好下，50％信号响应介于10％和90％信号之间。在不同风险偏好下，50％信号响应可能位于10％和90％之间的不同位置，但应该在所有神经元中都一样）。相反，分布RL预测，多巴胺神经元对50％信号的响应有所不同：某些神经元应该乐观地响应，发出的RPE几乎与90％信号一样大。其些应该悲观地做出响应，发出的RPE接近10％信号响应（图3a）。分布RL分别将这两种情况标记为乐观和悲观偏差，将其作为一个群体进行预测，多巴胺神经元应同时显示奖励概率的乐观和悲观编码。
为了测试此预测，我们分析了刚刚描述的信号概率任务中的多巴胺能VTA神经元的响应（更多详细信息，请参见方法）。正如分布RL预测的那样，但不是根据标准理论预测的，多巴胺神经元在三个奖励概率信号中的响应方式有所不同，观察到了乐观和悲观的概率编码（图3b左侧，扩展数据图6, 7）。同样，这种多样性不是由噪声引起的，因为在P<0.05的阈值下，31个细胞中有10个显著乐观，还有9个显著悲观。（见方法）相比之下，在0.05的阈值下，非分布TD系统中的31个细胞中大约有3个有望随机出现乐观或悲观的状态。在组这一级，单向方差分析（ANOVA）（F(30, 3335)=4.31，P=6×10-14）拒绝了无多样性的零假设。值得注意的是，在个体动物中同时观察到两种形式的概率编码。在记录的细胞数量最多的动物中，一致认为乐观的是17个细胞中的4个，而悲观的则是5个。在ANOVA（F(15, 1652)=4.02，P=3×10-7）下，这也很显著。
因为大多数细胞记录在不同的时间段中，所以重要的是要检查时间段之间奖励期望的全局变化是否可以解释观察到的乐观程度差异。为此，我们分析了预期舔食的模式。在这里，我们发现，尽管舔食时间段内波动预示着多巴胺细胞发放的时间段内波动，但在每个细胞的基础上，乐观与舔食之间没有关系（扩展数据图9）。该观察结果使得我们不可能在多巴胺神经元中观察到的各种响应通过总体奖励期望中的时间段间差异来解释。在一只动物中同时记录了多个细胞的情况下，观察到了反转点多样性这一事实进一步破坏了这种解释（图3c和补充信息）。
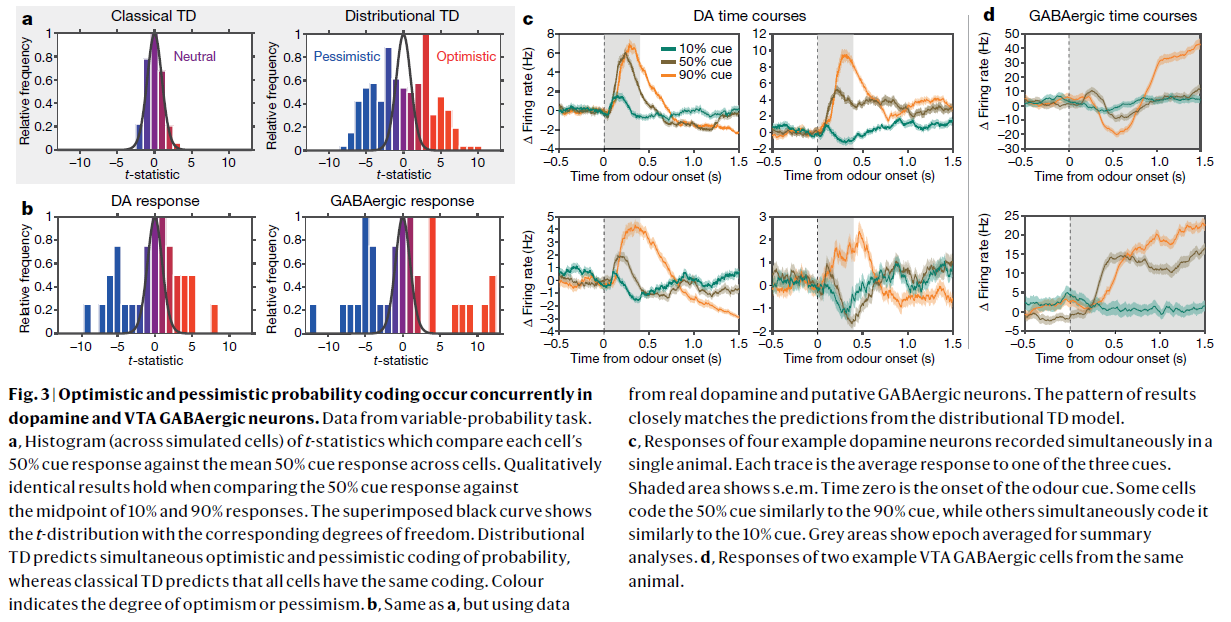
图3 | 在多巴胺和VTA GABAergic神经元中同时发生乐观和悲观概率编码。
数据来自可变概率任务。
a，t统计量的直方图（跨模拟细胞），用于比较每个细胞的50％信号响应与各个细胞的平均50％信号响应。将50％信号响应与10％和90％响应中点进行比较时，定性结果相同。叠加的黑色曲线显示了具有相应自由度的t分布。分布TD预测概率同时进行乐观和悲观编码，而经典TD预测所有细胞具有相同的编码。颜色表示乐观或悲观程度。
b，与a相同，但使用来自真实多巴胺和推测的GABAergic神经元的数据。结果的模式与分布TD模型的预测紧密匹配。
c，在单个动物中同时记录的四个示例多巴胺神经元的响应。每条轨迹线是对三个信号之一的平均响应。阴影区域显示均值标准误差。气味信号从时刻0开始。一些细胞按照类似于90％信号的方式编码50％信号，而一些细胞同时将其按照类似于10％信号的方式进行编码。灰色区域显示的时间段为摘要分析的均值。
d，来自同一动物的两个示例VTA GABAergic细胞的响应。
GABAergic neurons make diverse reward predictions
在分布RL中，由于不同的RPE通道监听不同的奖励预测，因此RPE信号出现了多样性，这因它们的乐观程度而异。从神经科学的角度来看，因此应该有可能追踪在VTA多巴胺神经元上已经确定的效应，回到发送奖励预测的上游神经元。先前的工作强烈表明，VTA GABAergic（γ-氨基丁酸）神经元恰好具有这种作用，并且用于计算RPE的奖励预测反映在其发放率上19。因此，我们预测，在上述相同任务中，VTA GABAergic神经元群体也应同时包含乐观和悲观概率编码。如预测的那样，在推定的GABAergic神经元之间观察到概率编码方面的一致性差异，同时存在乐观和悲观情况（图3b右侧）。在记录的细胞数量最多的动物中，36个细胞中有12个一致乐观，还有11个一致悲观（示例细胞如图3d所示）。
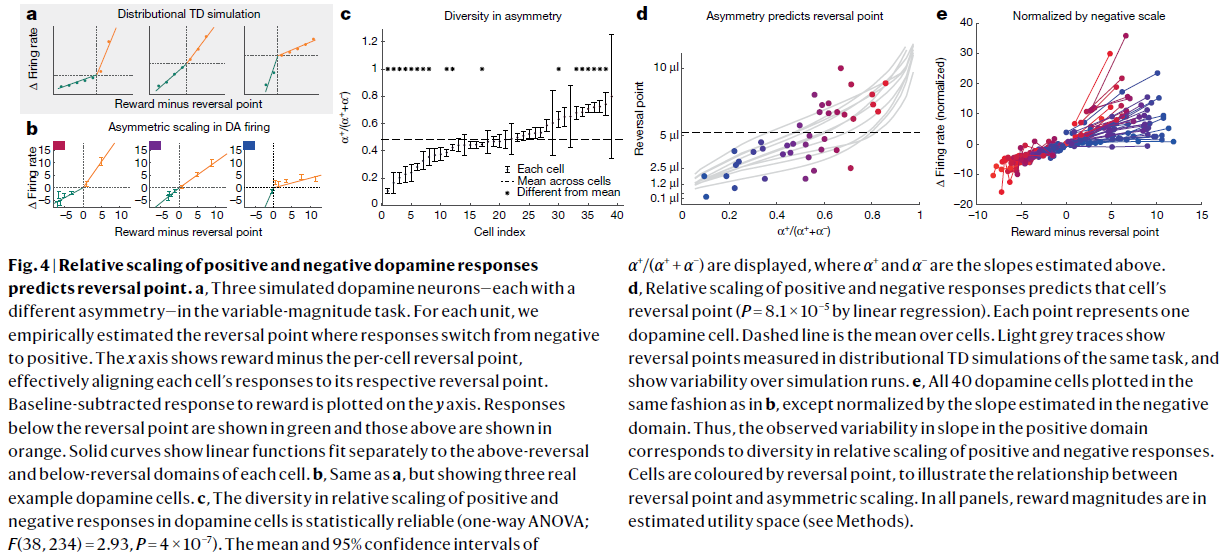
图4 | 多巴胺正负响应的相对比例可以预测逆转点。
a，在可变幅度任务中，三个模拟的多巴胺神经元，每个具有不同的不对称性。对于每个细胞，我们根据经验估计响应由负转正的反转点。x轴显示的是奖励减去每个细胞的反转点，从而有效地将每个细胞的响应与其各自的反转点对齐。在y轴上绘制的是减去基准的奖励响应。反转点以下的响应以绿色显示，上方的响应以橙色显示。实曲线显示线性函数分别在每个细胞的上方和下方区域进行拟合。
b，与a相同，但显示了三个真实的多巴胺细胞示例。
c，多巴胺细胞中正负响应的相对比例的多样性在统计学上是可靠的（单向ANOVA；F(38, 234)=2.93，P=4×10-7）。图中显示了α+/(α+ + α-)的均值和95％置信区间，其中α+和α-是上面估计的斜率。
d，正负响应的相对比例可以预测细胞的反转点（通过线性回归，P=8.1×10−5）。每个点代表一个多巴胺细胞。虚线是细胞上的均值。浅灰色的轨迹线显示了在同一任务的分布TD模拟中测得的反转点，并显示了模拟运行的可变性。
e，所有40个多巴胺细胞均以与b中相同的方式绘制，除了通过负域中估计的斜率归一化以外。 因此，在正域中观察到的斜率变化对应于正负响应的相对比例的多样性。细胞由反转点着色，以说明反转点和不对称缩放之间的关系。在所有子图中，奖励幅度都在估计的效用空间内（请参见方法）。
Distribution coding from asymmetric RPE scaling
前面各节中报告的结果表明，在RL基础的神经回路中编码了价值预测的分布。首先如何产生这种编码？在分布RL15上，最新AI研究表明，如果对经典TD学习机制进行一次更改，则分布编码会自动出现。
在经典TD中，正负误差的权重相等。作为结果，当学习的预测等于奖励分布的均值时，正负误差处于平衡状态。因此，经典TD学会预测未来奖励的均值。
相比之下，在分布TD中，不同的RPE通道在正或负的RPE上设置不同的相对权重（见图1b）。在正的RPE权重超出的通道中，要达到平衡，就需要减少这些正误差的发生频率，因此学习动力会集中在更乐观的奖励预测。相反，在通道中负的RPE权重超出的情况下，需要更悲观的预测才能达到平衡（图4a，扩展数据图1a）。跨所有通道学习的一组预测将对奖励分布的完整形状进行编码。
当将分布RL视为多巴胺系统的模型时，这些点转化为两个可检验的预测。首先，多巴胺神经元在正与负的RPE的相对比例上应该有所不同。为了测试此预测，我们分析了上述可变幅度任务中来自VTA多巴胺神经元的活动。我们首先估计了每个细胞的反转点，如前所述。然后，对于每个细胞，我们分别估计出两个斜率：α+用于正域（即高于反转点）的响应，而α-用于负域（图4b）。这揭示了在多巴胺神经元之间，正与负的RPE的相对幅度具有可重现差异（扩展数据图5）。在所有动物中，比率α+/(α++α-)的均值为0.48。 但是，许多细胞的值明显高于或低于该均值（图4c；有关统计检验的详细信息，请参见方法）。在组这一级，通过单向ANOVA（F(38, 234)=2.93，P=4×10-7），细胞之间存在显著差异。在记录的细胞数量最多的动物中，每15个细胞中有3个显著低于均值，也有3个显著高于均值。ANOVA再次拒绝了细胞之间没有多样性的零假设（F(14, 90)=4.06，P=2×10-5）。
其次，RPE的不对称性应在多巴胺神经元中与反转点相关。在斜率上正的RPE比负的RPE更高的多巴胺神经元应与相对乐观的奖励预测相关联，因此在相对较高的奖励幅度上具有反转点。在斜率上正的RPE更低的多巴胺神经元应该具有相对较低的反转点。再次使用来自可变幅度任务的数据，我们发现RPE不对称性与反转点之间具有很强的相关性（通过线性回归，P=8.1×10-5；图4d,e），验证了这一预测。此外，仅考虑来自记录的细胞数量最多的单只动物的数据时，这种效应仍然存在（P=0.002）。
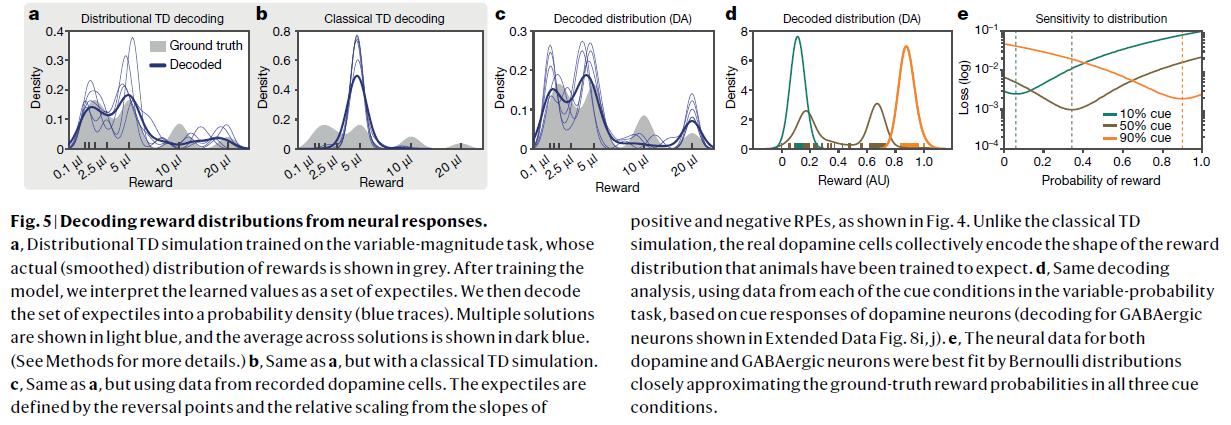
图5 | 从神经反应中解码奖励分布。
a，在可变幅度任务上训练的分布TD模拟，其实际（平滑）的奖励分布以灰色显示。训练模型后，我们将学习的价值解释为一组期望价值。然后，我们将期望集解码为概率密度（蓝色轨迹线）。多个解决方案以浅蓝色显示，所有解决方案的均值以深蓝色显示。（有关更多详细信息，请参见方法。）
b，与a相同，但具有经典的TD模拟。
c，与a相同，但使用记录的多巴胺细胞中的数据。如图4所示，由反转点和正与负的RPE的斜率的相对比例来定义期望。与传统的TD模拟不同，真实的多巴胺细胞共同编码训练过的动物期望得到的奖励分布的形状。
d，基于多巴胺神经元的信号响应（对扩展数据图8i,j中所示的GABAergic神经元进行解码），使用来自可变概率任务中每个信号条件中的数据的相同解码分析。
e，多巴胺和GABAergic神经元的神经数据都通过伯努利分布最接近地拟合，在三种情况下，伯努利分布都非常接近真实的奖励概率。
Decoding reward distributions
正如我们已经讨论过的，分布TD模型正确地预测多巴胺神经元应该显示出不同的反转点和响应不对称性，并且这些应该相关。最后，我们考虑模型的最详细的预测。在任何实验情况下观察到的特定反转点，以及相应神经元中的特定响应不对称性，都应编码对未来奖励中预期概率分布的近似表示。
如果是这种情况，那么在有足够数据的情况下，应该可以从多巴胺神经元的响应中解码出全部价值分布。作为分布RL假设的最终检验，我们尝试了这种类型的解码。分布TD模型意味着，如果多巴胺能响应在正负域中近似线性，则所得的学习奖励预测将对应于奖励分布的期望20（期望是分布的统计量，以类似于将中位数推广到分位数的方式推广均值）。
因此，我们将在可变幅度任务中测得的反转点和响应不对称定义为一组期望，并将这些期望转换为概率密度（请参见方法）。如图5a–c所示，所得的密度捕获了真实分布的多种模式。解码由分布TD仿真而不是经典TD仿真生成的RPE，可以得到相同的结果模式。
侧重于可变概率任务的并行分析（请参见方法）与该任务中的真实分布有相似的良好匹配（图5d,e）。在这两个任务中，成功的解码取决于神经数据中可变性的特定模式，而不取决于可变性本身的存在（扩展数据图8）。
值得强调的是，多巴胺的标准RPE理论并没有预见到我们所提到的任何效应，该理论意味着所有多巴胺神经元都应该传递基本相同的RPE信号。为什么以前没有观察到目前的效应？在某些情况下，相关数据一直隐藏不明。例如，许多研究提到了跨多巴胺神经元的正与负的RPE的相对大小存在显著差异。但是，他们将其视为偶然发现或测量误差的反映，或将其视为RPE理论的问题17。对多巴胺能RPE中奖励概率编码的最早研究之一表明，多巴胺神经元之间存在显著差异，但仅在脚注中18。一个更普遍的问题是，我们提到的变种形式被传统的分析技术所掩盖，传统的分析技术通常侧重于多巴胺神经元的平均响应（参见补充信息和扩展数据图10）。
分布RL提供了一系列未经测试的预测。多巴胺神经元在整个任务情景中应保持相对乐观程度的次序，即使奖励的具体分布发生了变化。如果通过光遗传学选择性激活具有特定乐观程度的RPE通道，则应该塑造学习到的分布，然后通过对分布时刻敏感的行为度量来检测到该分布。 们在补充信息中列出了进一步的预测。
分布RL也引起了许多更广泛的问题。在正与负的RPE尺度中引起不对称多样性的电路级或细胞级机制是什么？还值得考虑的是，除了RPE的不对称缩放以外，其他机制是否也可能有助于分布编码。例如，众所周知，正与负的RPE差异地参与纹状体D1和D2多巴胺受体21，并且这些受体的平衡在解剖学上也有所不同22-24。这表明了从正与负的RPE进行差异学习的第二种潜在机制25。此外，不同的RPE通道在解剖学上如何与它们相应的奖励预测相结合（请参见扩展数据图4i-k）？最后，在动作学习和选择上，分布编码会对下游产生什么影响？考虑到这个问题，值得注意的是，行为经济学中的一些当前理论围绕着风险度量，这些风险度量可以很容易地从本工作已经考虑的分布编码中推导出。
最后，我们推测了多巴胺分布假说对成瘾和抑郁症等精神疾病机制的影响。情绪与未来回报的预测相关联26，有人提出抑郁症和双相情感障碍都可能涉及对价值影响的结果的偏差预测27。最近有人提出，这种偏差可能是由RPE编码中的不对称引起的28,29。这些想法与我们在此处提到的现象之间存在明显的潜在联系，这为进一步研究提供了机会。
Online content
任何方法，其他参考资料，Nature Research报告摘要，源数据，扩展数据，补充信息，确认书，同行评审信息；作者贡献和竞争利益的详细信息；有关数据和代码可用性的声明，请访问https://doi.org/10.1038/s41586-019-1924-6.
Methods
Distributional RL model
我们在整个工作中使用的分布RL模型基于非对称回归原理，并扩展了AI中的最新结果5,6,15。我们在补充信息中提供了有关分布RL的更详细且易于访问的介绍。在这里，我们简要概述该方法。
令f：ℝ→ℝ为响应函数。在每个观察状态x中，让一组价值预测Vi(x)随学习率
更新。然后在给定状态x，下一个状态x'，结果奖励信号r和时间折扣γ∈[0, 1)的情况下，分布TD模型计算分布TD误差：
其中Vj(x')是分布V(x')中的样本。然后，模型使用下式更新基准：
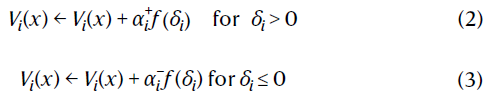
当以表格形式执行，不对称均匀分布且f(δ)=sgn(δ)时，此方法收敛到x上折扣奖励分布的τi分位数，
（参考文献6）。同样，响应函数为f(δ)=δ的不对称回归对应于期望回归31。像分位数一样，期望充分地说明了分布的特征，并且已被证明对风险度量尤其有用32,33。
最后，我们注意到在整篇论文中，我们使用乐观和悲观术语来指高于或低于平均（期望）回报的回报预测。重要的是，从一组可能的结果中，这些预测对应特别好的结果是乐观的，对应无法令人满意的结果是不乐观的。
Ref 8: https://zhuanlan.zhihu.com/p/35245722
Artificial agent results
使用公开可用的Arcade学习环境34，Atari的结果处于Atari-57基准上。这是一组57个Atari 2600游戏和人类性能基准。有关深度Q网络（DQN）和人为归一化分数计算的详细信息，请参阅先前的工作8。分布TD智能体使用我们提出的模型和具有多个（n=200）价值预测器的DQN，每个价值预测器具有不对称性，并且均匀地隔开[0, 1]。 DQN的训练目标（Huber损失）被非对称分位数Huber损失所代替，它对应于κ饱和响应函数f(δ)=max(min(δ, κ), -κ），其中κ=1。
最终，在每次更新时，我们都基于即时奖励和来自所有下一状态的价值预测器的未来奖励预测来训练所有通道。进一步的细节可以在参考资料6中找到。基于物理的电机控制任务需要控制28个自由度的人形物，以在最短的时间内完成3D障碍物航向35。D3PG和分布D3PG智能体的完整详细信息如参考工作所述14。扩展数据图2d,f中显示回报分布基于给定帧中每个网络的网络预测分布。
Tabular simulations
经典TD和分布TD模型的表格模拟使用了均匀随机选择的学习率群，其中对每个细胞 i，
。在所有情况下，经典TD模型与分布TD模型之间的唯一算法差异是，分布模型对负预测误差使用了单独变化的学习率，其中对每个细胞 i，
。两种方法都使用线性响应函数。在其他响应函数（例如，Hill函数30或κ饱和）上也获得了定性相似的结果，尽管这些导致了分布的不同语义估计。选择群大小是为了清楚表达并提供与神经元数据中观察到的相似的可变性。每个细胞都与不同的状态相关价值估计Vi(x)配对。请注意，尽管这些模拟专注于即时奖励，但相同的算法还可以学习多步回报的分布。
在可变概率任务中，每个信号对应于不同的价值估计和奖励概率（90％，50％或10％）。当获得奖励时，智能体获得的奖励值为1.0；当没获得奖励时，智能体获得的奖励值为0.0。两种智能体均接受了5000次更新的100次试验的训练，并且都模拟了n=31个细胞（单独的价值估算）。所有学习率均在[0.001, 0.2]之间随机选择。信号响应被视为从恒定零基准到价值估计的时序差分。
在可变幅度任务中，所有奖励均视为以μl为单位的水量（使用效用而不是幅度获得定性相同的结果）。对于图2，我们针对150个估计量进行了10个试验，每个试验25000个更新，随机学习率分别为[0.001, 0.02]。 这些较小的学习率和大量更新旨在确保这些价值完全收敛且误差很小。然后，我们报告十个细胞的时序差分误差，这些误差一致地采用以跨越每个智能体的价值估计范围。报告的误差（模拟发放率的变化）是奖励效用减去价值估算值，并根据学习率进行缩放。与神经元数据一样，这些数据是在试验中平均的，并通过奖励幅度的方差进行归一化。分布TD的RPE是使用非对称学习率计算的，学习率中添加了一个较小的常数（向下取整）。
Distribution decoding
对于真实的神经数据和TD模拟，我们执行了分布解码。用于在可变幅度任务中进行解码的分布和经典TD仿真，每个都使用40个价值预测器，以匹配神经数据中的40个记录细胞（对六只动物进行了神经分析）。在分布TD模拟中，每个价值预测器使用不同的不对称缩放因子
，因此学习了不同的价值预测Vi。
解码分析从一组反转点Vi和不对称缩放因子τi开始。对于神经数据，如其他地方所述获得这些数据。对于模拟，可以直接从模拟中读取它们。这些数字被解释为一组期望，τi-th期望为Vi。通过解决优化问题以找到与期望集最兼容的密度，我们将它们解码为概率密度20。为了优化，将密度参数化为一组样本。为了在图5中显示，使用核密度估计对样本进行了平滑处理。
Animals and behavioural tasks
我们在这里重新分析的啮齿动物数据首先在参考文献19中报道。方法的详细信息可以在该论文和参考文献30中找到。我们简要介绍以下方法。
对五只老鼠进行了“可变概率”任务训练，而对六只不同的老鼠进行了“可变幅度”任务训练。在可变概率任务中，在每个试验中，动物首先经历四种气味信号之一，持续1s，然后暂停1s，然后进行奖励（3.75μl水），厌恶的气喘或什么都不做。气味1表示有90％的机会获得奖励，气味2表示有50％的机会获得奖励，气味3表示有10％的机会获得奖励，而气味4则表示有90％的机会出现气喘。气味的含义在动物之间是随机的。试验内间隔是指数分布的。
将红外线束放置在注水口的前面，并且记录每个束中断为一次舔食事件。我们报告在信号和结果之间的整个时间间隔内（即信号发生后的0–2000ms）的平均舔食率。
在可变幅度的任务中，在10％的试验中，发出了气味信号，表明该试验不会产生任何奖励。在其余90％的试验中，随机提供以下奖励幅度之一：0.1, 0.3, 1.2, 2.5, 5, 10或20μl。在这些试验的一半中，该奖励之前有1500ms的气味信号（这表明即时奖励，但未透露其强度）。在另一半，它没有信号。
为了在记录时识别多巴胺神经元，通过将以Cre依赖性方式表达ChR2的腺相关病毒（AAV）注入表达Cre重组酶的转基因小鼠的VTA中，在多巴胺转运蛋白（DAT）基因Slc6a3(B6.SJL-Slc6a3tm1.1(cre)Bkmn/J，The Jackson Laboratory)36的启动子下，用channelrhodopsin-2（ChR2）标记VTA中的神经元。 如所述37，将小鼠植入头板和定制的微型驱动器，该驱动器包含6-8个四极体（Sandvik）和光纤。
所有实验均按照美国国立卫生研究院实验动物的护理和使用指南进行，并得到哈佛大学动物护理和使用委员会的批准。
Neuronal data and analysis
使用数据采集系统（DigiLynx，Neuralynx）从VTA进行细胞外记录。VTA记录部位经过组织学验证。通过记录细胞对短暂的蓝光脉冲序列的电生理响应来证实多巴胺能细胞的身份，该脉冲序列仅刺激表达DAT的细胞。使用SpikeSort3D（Neuralynx）或MClust-3.5（A.D. Redish）对脉冲进行分类。如前所述30,37，通过发放模式的聚类确定了VTA中假定的GABAergic神经元。所有置信区间均为均值标准误差，除非另有说明。
使用NumPy 1.15和MATLAB R2018a（Mathworks）进行数据分析。脉冲时间收集在1ms的容器中，以创建刺激时间直方图。然后，通过与函数
进行卷积来平滑这些直方图，其中T是一个时间常数，如参考文献30中所述设置为20ms。对于单细胞跟踪，出于显示目的，我们将T设置为200ms。
平滑后，通过从每个试验和每个神经元中减去相对于刺激发生（或相对于意外的奖励条件下的奖励发生）从-1000到0ms的该试验活动的均值进行基准校正。
Variable-probability task. 从五只动物中记录n=31个细胞，每只动物具有以下数目的细胞：1, 4, 16, 1和9。多巴胺神经元对信号的响应定义为信号开始后0到400ms的平均活动。选择此间隔以匹配参考文献30。假定的GABAegic神经元对信号的响应定义为信号开始后0-1500ms的平均活动。选择较长的时间间隔是因为这些神经元的响应要慢得多，通常在信号发生后的最初500或1000ms内缓慢增加（图3d）。
我们对50％信号的响应中是否存在细胞间多样性感兴趣。我们首先将每个细胞对50％信号的响应进行归一化，如下所示：
= (c50 - mean(c10)) / (mean(c90) - mean(c10))，其中均值表示在一个细胞内对各试验进行平均。为了不了解动物的风险偏好，我们随后对所有细胞对50％信号的归一化响应的均值进行了two-tailed t检验，以测试该细胞对50％信号的归一化响应。这是对我们在正文中报告的乐观或悲观概率编码的检验。请注意，如果细胞之间的差异是偶然的，则这些t统计量将是t分布的。我们还报告了ANOVA结果，其中我们评估了所有细胞归一化的50％响应均具有相同均值的零假设。
相反，将对50％信号的响应与对10％信号的响应与对90％信号的响应之间的中点进行比较时，结果的模式相同。
将扩展数据图7中显示的每个细胞信号应归一化为零均值和单位方差，以允许直接比较具有不同响应可变性的细胞。根据两个single-tailed Mann-Whitney测试的结果，每个细胞出现在三个面板之一中，该测试评估了c10<c50和c50<c90的排列顺序（更多信息，请参见补充信息第3.3节）。左，中和右面板分别对应于结果(P≥0.05, P<0.05), (P<0.05, P<0.05或P≥0.05, P≥0.05)和(P<0.05, P≥0.05)。
Variable-magnitude task. 从五只动物中记录了n=40个细胞，每只动物具有以下数目的细胞：3, 6, 9, 16和6。对奖励的响应定义为奖励开始后200到600ms内的平均活动。选择该时间间隔以尽可能接近地匹配参考文献30，同时排除对饲养者点击的初始响应30,38,39，它对奖励幅度没有选择性，对所有奖励幅度都是正值。这使我们能够找到相对于基准增强或抑制多巴胺响应的奖励幅度。
每个细胞的反转点（即不会引起相对于基准发放的正偏离或负偏离的奖励幅度）被定义为MR幅度，该幅度最大化大于MR的奖励的正响应的数量加上对小于MR的奖励的负响应的数量。为了获得反转点上细胞间差异可靠性的统计信息，我们将数据划分为随机的一半，并分别估计了每个细胞在每一半中的反转点。我们使用不同的随机划分将该程序重复了1000次，并报告了这1000折的平均R值和几何平均p值。
测量反转点后，我们将线性函数分别拟合到每个细胞的正与负域。为了获得置信区间，我们将数据划分为七个随机划分（七个是任何条件下任何细胞中最小的试验次数），但要受每个细胞的每个条件在每个划分中至少包含一个试验的约束。在每个划分中，我们都重复估计反转点并在正与负域中查找斜率的过程。那么我们在
上的置信区间为七个划分中计算出的价值的均值标准误差。ANOVA也有报道测试了零假设，即细胞之间（跨划分）的均值不变。
使线性函数适合多巴胺响应，在效用空间比在奖励量空间更合乎逻辑。我们依靠参考文献38从多巴胺响应到不同幅度的奖励近似潜在的效用函数。我们使用这些经验效用代替原始奖励幅度进行图4所示的分析。但是，没有报告的结果对效用函数的选择敏感。我们还使用其他效用函数进行了分析，这些结果在扩展数据图5中进行了报告。图5中的分析未包括一个细胞：因为它对任何奖励幅度均无正响应，所以斜率无法拟合在正域。
在测量反转点与τ之间的相关性（跨细胞）时，我们首先将数据随机分为两个不相交的试验。在一半中，我们首先计算了反转点RP1并使用这些反转点来计算α+和α-。在另一半中，我们计算了反转点RP2。 我们报告的相关性在RP2和τ=α+/(α+ + α-)之间。我们这样做是为了避免与使用相同数据来估计斜率和截距有关的混淆。
Reporting summary
有关研究设计的更多信息，请参见与本文链接的《自然研究报告摘要》。
Data availability
这项工作中分析的神经元数据可在以下网址获得：https://doi.org/10.17605/OSF.IO/UX5RG.
Code availability
我们的价值分布解码的分析编码和用于生成分布TD模型预测的编码可在以下位置获得：https://doi.org/10.17605/OSF.IO/UX5RG.
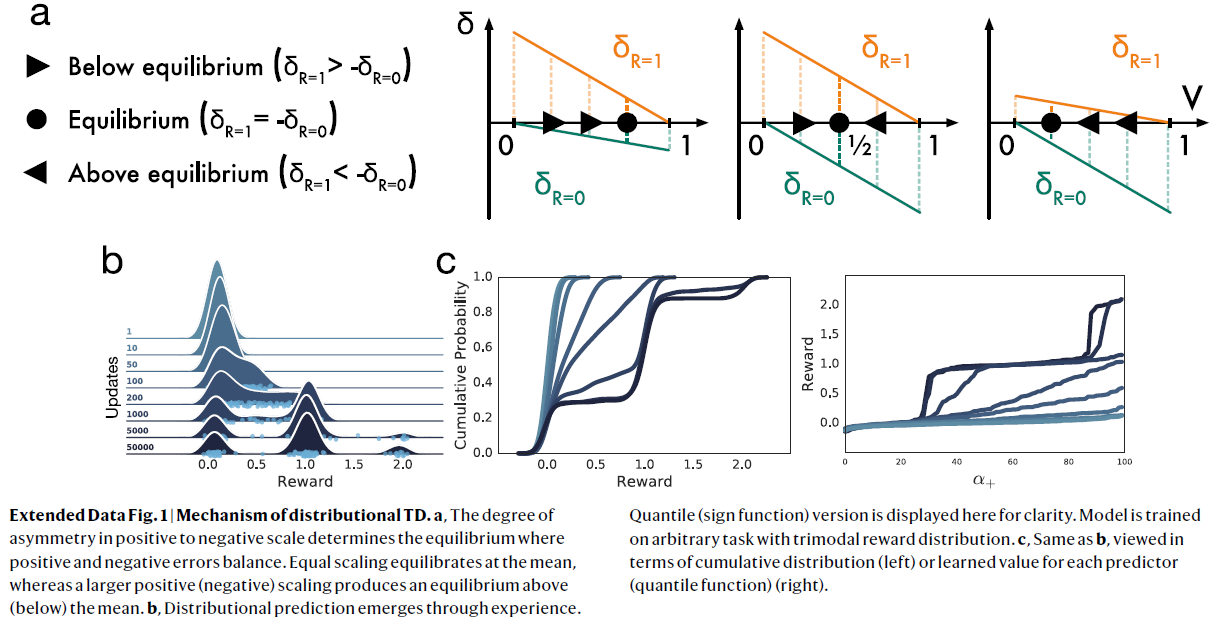
扩展数据图1 | 分布TD的机制。
a，正负比例的不对称程度决定了正负误差平衡。相等的缩放比例在均值处达到平衡，而较大的正（负）缩放比例会在均值上方（下方）产生平衡。
b，分布预测来自经验。为清楚起见，此处显示分位数（符号函数）版本。在具有三峰奖励分布的任意任务上训练模型。
c，与b相同，从累积分布（左侧）或每个预测器的学习价值（分位数函数）（右侧）的角度来看。
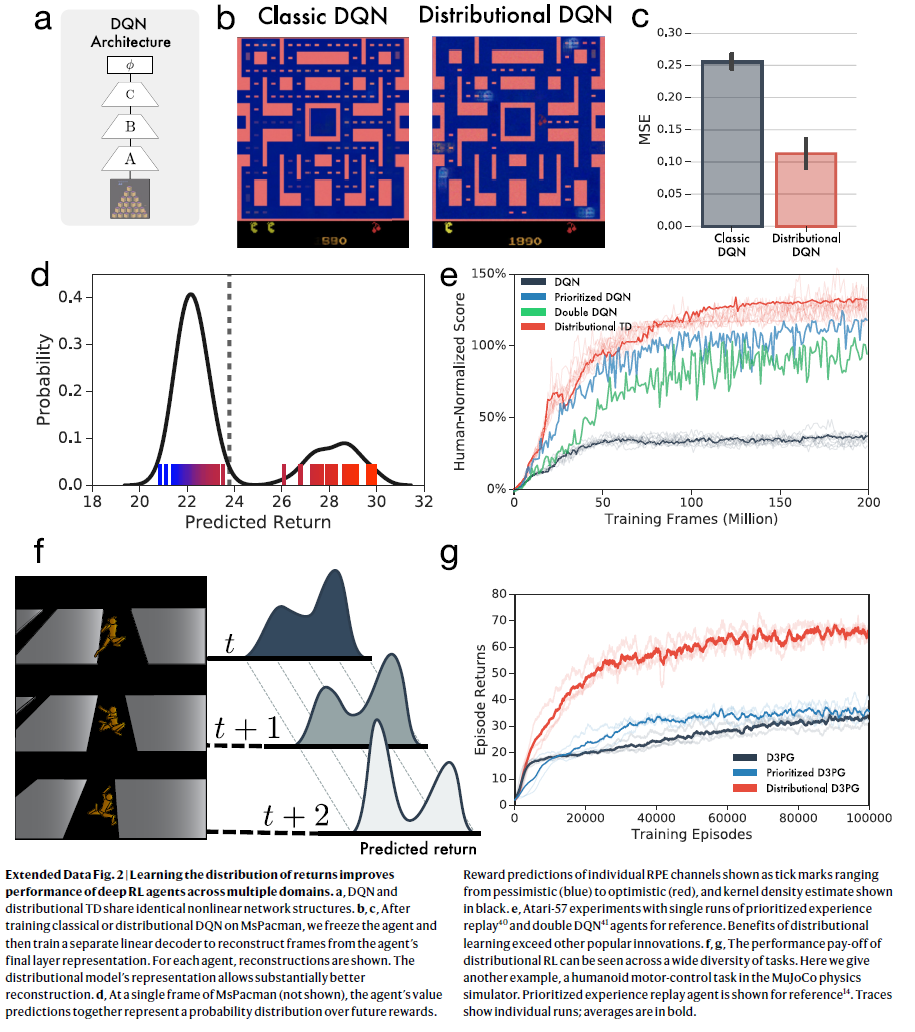
扩展数据图2 | 了解回报分布可提高深度RL智能体跨多个域的性能。
a，DQN和分布TD共享相同的非线性网络结构。
b，c，在MsPacman上训练了经典或分布DQN之后，我们冻结了智能体，然后训练了一个单独的线性解码器，以从智能体的最终层表征中重构帧。对于每个智能体，都显示了重构。分布模型的表征可以显着改善重构效果。
d，在MsPacman的单个帧（未显示）上，智能体的价值预测共同代表了未来奖励的概率分布。单个RPE通道的奖励预测显示为刻度线，范围从悲观（蓝色）到乐观（红色），核密度估计以黑色显示。
e，Atari-57实验，该实验具有优先经验回放40和双重DQN41智能体以供参考。 分布学习的好处超过了其他流行的创新。
f，g，分布RL的性能收益可以在各种各样的任务中看到。在这里，我们给出另一个示例，即MuJoCo物理模拟器中的人形机器人控制任务。图中显示了优先经验回放智能体，以供参考14。轨迹显示单个运行；均值以粗体显示。
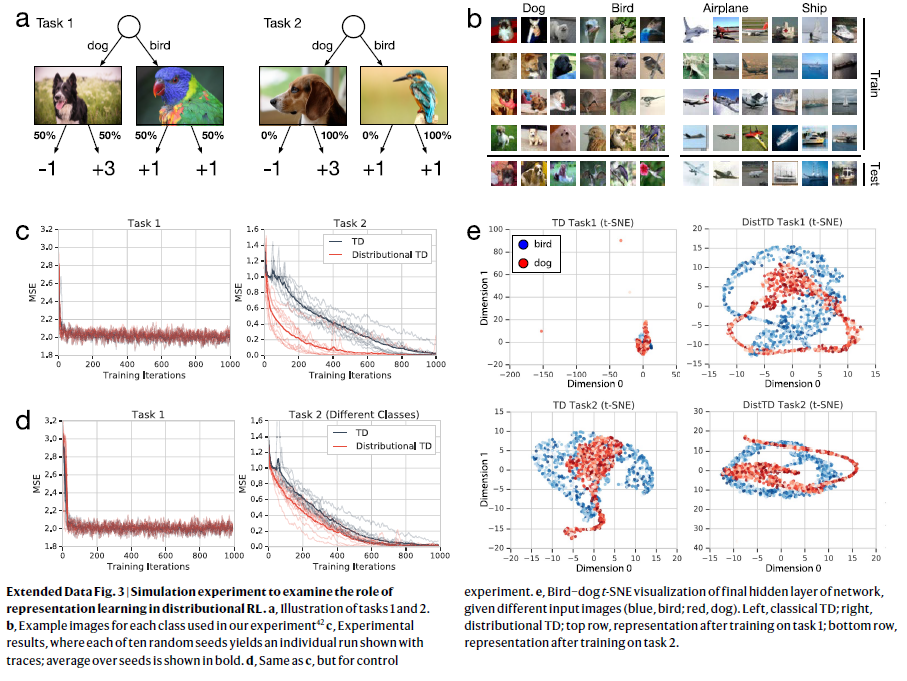
扩展数据图3 | 通过仿真实验来检验表征学习在分布RL中的作用。
a，任务1和2的图示。
b，实验中使用的每个类别的示例图片42。
c，实验结果，其中十个随机种子中的每一个都产生一个带轨迹的单独运行；种子的均值以粗体显示。
d，与c相同，但用于对照实验。
e，给定不同的输入图像（蓝色，鸟；红色，狗），对网络的最终隐藏层使用鸟-狗 t-SNE可视化。左侧，经典TD；右侧，分布TD； 第一行，经过任务1训练后的表征；最下面一行，经过任务2训练后的表征。
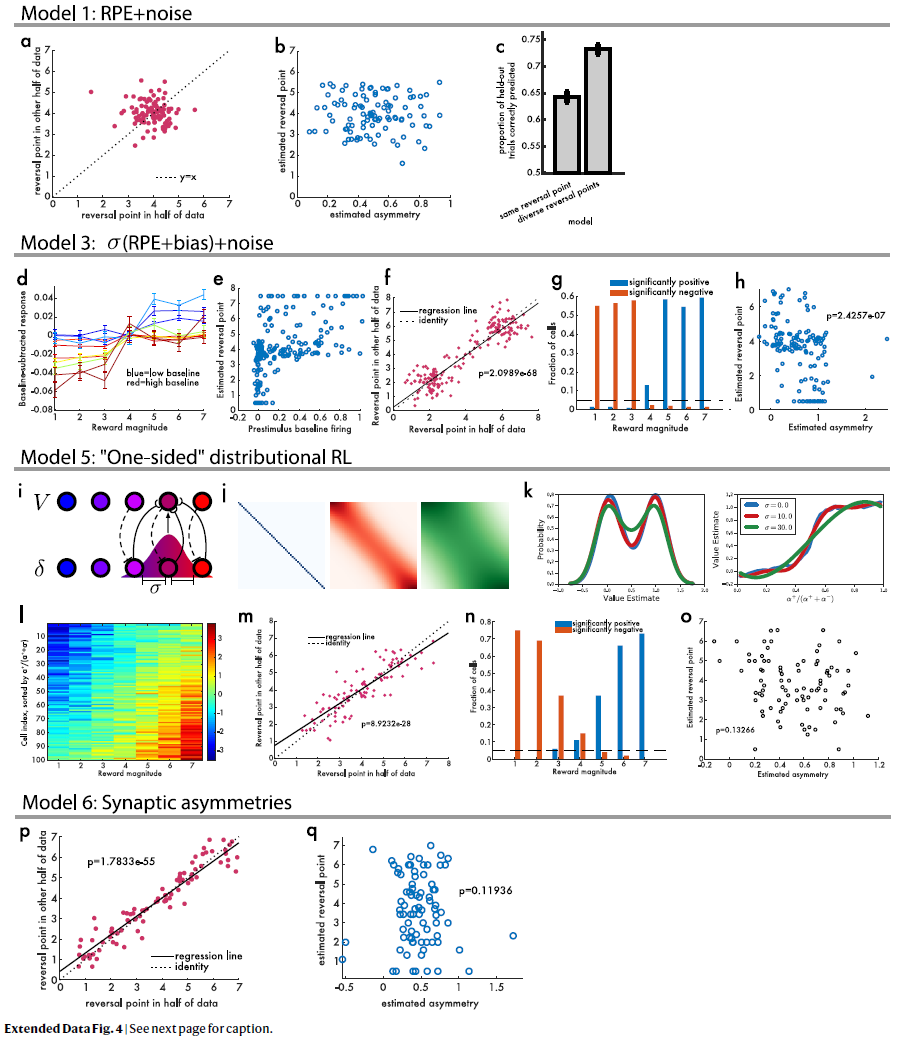
扩展数据图4 | 空模型。
a，经典TD加上噪声不会导致在可变幅度任务中的实际多巴胺数据中观察到的结果模式。当在两个独立的划分中估计反转点时，两者之间没有相关性（线性回归P=0.32）。
b，然后我们估计响应的不对称缩放，发现该点与反转点之间没有相关性（线性回归P=0.78）。
c，“相同”（单个反转点）与“多样化”（独立的反转点）之间的模型比较。在这两种模型中，该模型均用于预测坚持试验是否有正或负响应。
d，模拟减去基准的RPE，根据添加到该细胞RPE上的偏差真实值进行颜色编码。
e，在所有模拟细胞中，刺激前基准发放与估计的反转点之间存在很强的正相关关系。
f，两个独立的反转点测量值密切相关。
g，具有显著正（蓝色）或负（红色）响应的模拟细胞的比例在正与负响应中均未显示大小。
h，在仿真中，每个细胞的估计不对称性与其估计的反转点之间存在显著的负相关关系（与神经数据中观察到的相反）。
i，该图说明了RPE和价值预测器之间的高斯加权拓扑映射。
j，改变此高斯的标准偏差可调节耦合度。
k，在具有相等的机会获得1.0或0.0奖励的任务中，具有不同耦合级别的分布TD对耦合程度显示出鲁棒性。
l，当没有耦合时，不会学习分布编码，但是不对称缩放会导致对各种反转点的虚假检测。
m，即使每个细胞都具有相同的奖励预测，它们似乎具有不同的反转点。
n，使用此模型，某些细胞可能会对相同的奖励做出明显的正响应，而另一些则明显出现负响应。
o，但是该模型无法解释非对称缩放和反转点之间的正相关。
p，“突触式”分布RL的模拟，其中学习率而不是发放率是不对称缩放的。该模型预测多巴胺神经元之间反转点的多样性。
q，该模型预测发放率的不对称缩放与反转点之间没有相关性。
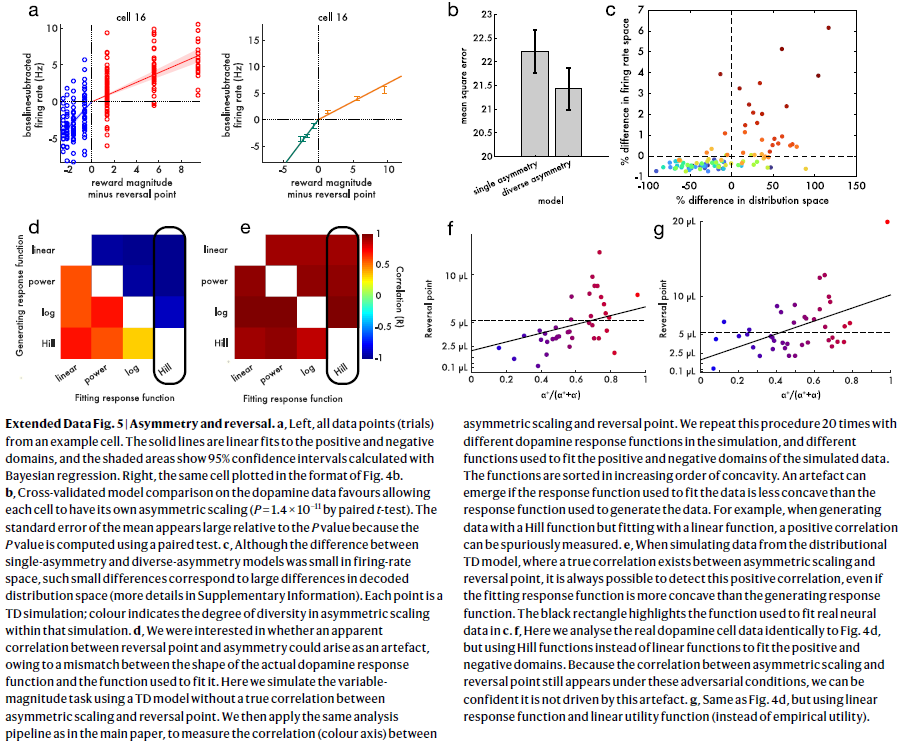
扩展数据图5 | 不对称和反转。
a，左侧，来自示例细胞的所有数据点（试验）。实线是对正与负域的线性拟合，并且阴影区域显示使用贝叶斯回归计算的95％置信区间。右侧，同一细胞以图4b的格式绘制。
b，对多巴胺数据的交叉验证模型比较有利于使每个细胞具有自己的不对称缩放比例（通过配对t检验，P=1.4×10-11）。均值标准误差相对于P值似乎较大，因为P值是使用配对检验计算的。
c，尽管单不对称模型和多样不对称模型之间的差异在发放率空间中很小，但这种较小差异对应于解码后的分布空间中的较大差异（补充信息中有更多详细信息）。每个点都是TD模拟；颜色表示该模拟中非对称缩放的多样性程度。
d，我们感兴趣的是，由于实际的多巴胺响应函数的形状和用于拟合它的函数之间的不匹配，在反转点和不对称性之间是否可能出现明显的相关性。在这里，我们使用TD模型模拟可变幅度任务，而在非对称缩放和反转点之间没有真正的相关性。然后，我们使用与主论文中相同的分析流水线，以测量不对称缩放和反转点之间的相关性（色轴）。我们在模拟中使用不同的多巴胺响应函数重复此过程20次，并使用不同的函数拟合模拟数据的正负域。这些函数按凹面的升序排列。如果用于拟合数据的响应函数比用于生成数据的响应函数凹度小，则会出现伪影。例如，当生成具有Hill函数但与线性函数拟合的数据时，可以虚假地测量正相关。
e，当模拟来自分布TD模型的数据时，在非对称缩放和反转点之间存在真正的相关性，即使拟合响应函数比生成响应函数更凹，也始终可以检测到此正相关。黑色矩形突出显示了用于在c中拟合实际神经数据的函数。 f，这里我们与图4d相同地分析了实际的多巴胺细胞数据，但是使用Hill函数而不是线性函数来拟合正负域。 由于在这些对抗条件下仍会出现不对称缩放和反转点之间的相关性，因此我们可以确信它不受此伪影的影响。
g，与图4d相同，但使用线性响应函数和线性效用函数（而不是经验效用）。
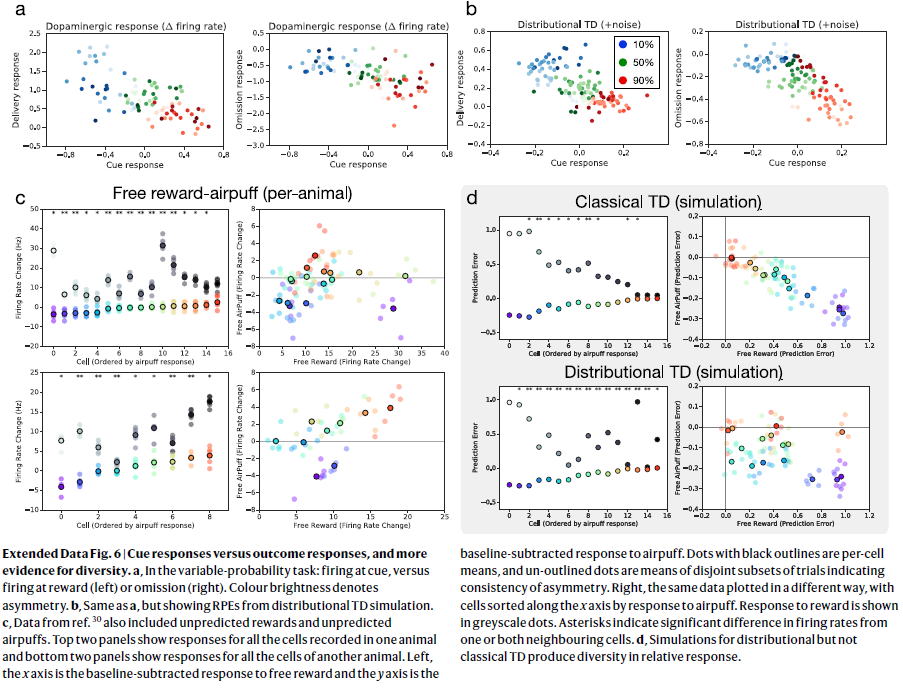
扩展数据图6 | 信号响应与结果响应，以及更多的多样性证据。
a，在可变概率任务中：信号发放，而不是奖励发放（左侧）或忽略发放（右侧）。颜色亮度表示不对称。
b，与a相同，但显示了来自分布TD仿真的RPE。
c，来自参考资料30的数据还包括意外的奖励和意外的吹气。顶部的两个面板显示了对一只动物中记录的所有细胞的响应，底部的两个面板显示了对另一只动物的所有细胞的响应。左图，x轴是减去自由奖励的基准响应，y轴是减去气喘的基准响应。黑色轮廓的点是每个细胞的均值，无轮廓的点是表示不对称一致性的不相交试验子集的均值。正确的是，相同的数据以不同的方式绘制，细胞根据气喘的响应沿x轴排序。对奖励的响应以灰度点表示。星号表示来自一个或两个相邻细胞的发放率的显著差异。
d，对分布TD而不是经典TD的仿真在相对响应中产生了多样性。
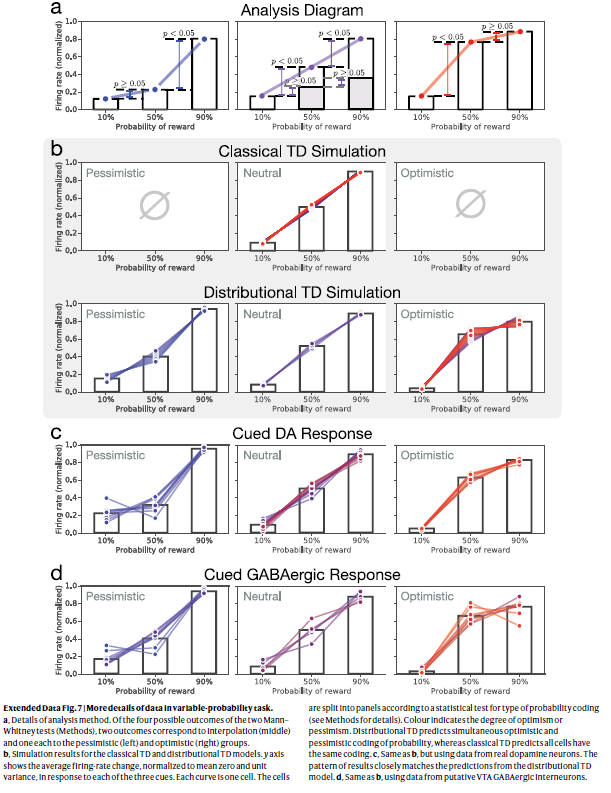
扩展数据图7 | 可变概率任务中数据的更多详细信息。
a，详细的分析方法。在两次Mann–Whitney检验（方法）的四个可能结果中，两个结果分别对应于插值（中间），一个分别对应于悲观（左侧）和乐观（右侧）组。
b，经典TD和分布TD模型的仿真结果。y轴显示了响应于三个信号中的每一个的平均发放率变化（归一化为零均值和单位方差）。每条曲线是一个细胞。根据用于概率编码类型的统计测试，将细胞划分为多个面板（有关详细信息，请参见方法）。颜色表示乐观或悲观的程度。分布TD预测概率同时进行乐观和悲观编码，而经典TD预测所有细胞具有相同的编码。
c，与b相同，但是使用来自真实多巴胺神经元的数据。结果的模式与分布TD模型的预测紧密匹配。
d，与b相同，使用来自推定的VTA GABAergic神经元间的数据。
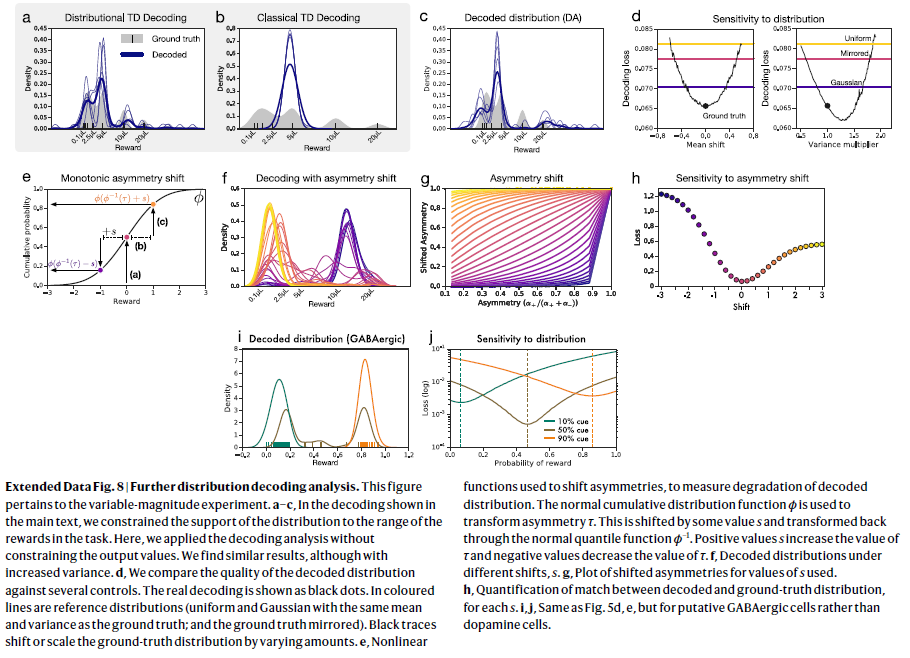
扩展数据图8 | 进一步的分布解码分析。
该图与可变幅度实验有关。
a–c，在正文所示的解码中，我们将分布的支持限制为任务中奖励的范围。在这里，我们在不限制输出价值的情况下应用了解码分析。尽管增加了方差，我们发现相似的结果。
d，我们将解码分布的质量与多个控件进行比较。实际解码显示为黑点。在彩色线中是参考分布（均匀分布和高斯分布，其均值和方差与基本事实相同，并且基本事实被镜像）。黑色轨迹可改变或缩放真实分布的数量。
e，非线性函数，用于转移不对称性，以测量解码分布的劣化。 正态累积分布函数ϕ用于变换不对称性τ。它被偏移了一些值s，并通过普通分位数函数ϕ-1变回了原样。 正值s增加τ的值，负值减小τ的值。
f，不同移位s下的解码分布。
g，所用s值的偏移不对称图。
h，对于每个s，解码的分布与真实分布之间的匹配量化。
i，j，与图5d,e相同，但适用于假定的GABAergic细胞而不是多巴胺细胞。
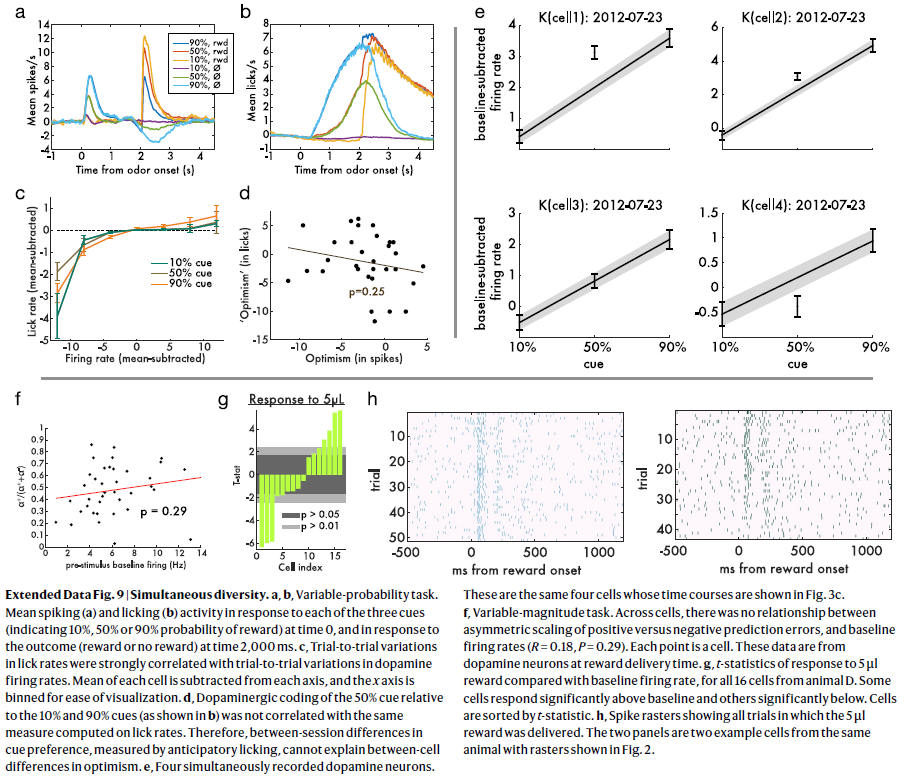
扩展数据图9 | 同时的多样性。
a，b，可变概率任务。在0时刻响应三个信号中的每个信号（表示奖励的概率为10％，50％或90％）并在2000ms时刻响应结果（奖励或无奖励）时，平均脉冲（a）和舔食（b）活动。
c，舔食率的试验间变化与多巴胺发放率的试验间变化密切相关。从每个轴中减去每个细胞的均值，并对x轴进行容器划分以便于可视化。
d，相对于10％和90％信号（如b中所示）的50％信号的多巴胺能编码与按舔食率计算出的相同测量值无关。因此，通过预期舔食测量的信号偏好之间的时间段间差异不能解释乐观的细胞间差异。
e，四个同时记录的多巴胺神经元。这些是相同的四个细胞，其时间进程如图3c所示。
f，可变幅度任务。在整个细胞中，正负预测误差的不对称缩放与基准发放率之间没有关系（R=0.18，P=0.29）。每个点都是一个细胞。这些数据来自奖励发送时的多巴胺神经元。
g，来自动物D的所有16个细胞与基准发放率相比，对5μl奖励的响应的t统计量。一些细胞的响应显著高于基准，而另一些则显著低于基准。细胞按t统计量排序。
h，脉冲栅格显示了所有提供5μl奖励的试验。这两个面板是来自同一只动物的两个示例细胞，其栅格如图2所示。
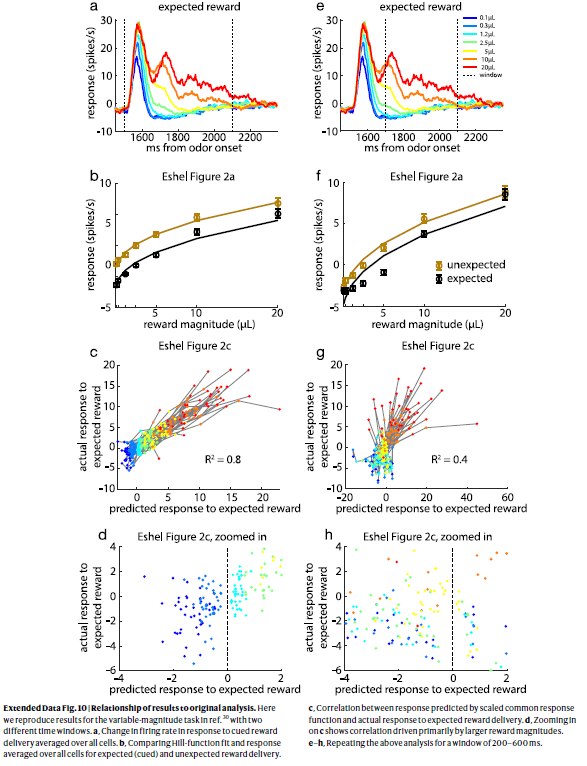
扩展数据图10 | 结果与原始分析的关系。
在这里，我们重现了参考文献30中可变幅度任务的结果，这带有两个不同的时间窗口。
a，响应于信号的奖励发送的平均发放率在所有细胞上的变化。
b，比较所有细胞的Hill函数拟合度和响应度，以得到预期（信号）和意外的奖励发送。
c，按比例缩放的通用响应函数预测的响应与对预期奖励发送的实际响应之间的相关性。
d，放大c表示相关性主要由较大的奖励幅度驱动。
e–h，在200–600ms的窗口中重复上述分析。
