郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！
原文链接：https://arxiv.org/pdf/2005.05941.pdf
1 Reinforcement learning with a network of spiking agents
2.0.2 Learning by reinforcement in spiking neural networks
3 Background, Preliminaries and Notation
3.2 Policy gradient algorithms
3.4 Conjugate Markov Decision Processes
3.5 Policy Gradient Coagent Networks
4 Designing the neural agent: spiking neuron models
4.1 Memoryless Ising model of spiking neuron
4.1.1 PGCN update emulates Hebbian/Anti-Hebbian learning in Ising model of spiking neurons
4.2 Stochastic Leaky Integrate & Fire Neuron
4.2.1 PGCN update emulates STDP learning in Leaky-Integrate-Fire model of spiking neurons
4.3 Generalized Linear Model of a Spiking Neuron
4.4 Linear-nonlinear-Poisson cascade neuron model
5 PGCN learning rule for a network of GLM spiking agents
6 Performance enhancement through variance reduction
6.1 Variance reduction through a modular connectionist architecture
6.2 Variance reduction through population coding
7 Reparameterization trick in spiking neural networks
7.3 Reparameterization through gumbel-softmax
7.4 Spiking neuron as a stochastic node
8.1 Reinforcement learning domains
8.2.1 PGCN learning in gridworld with a memoryless spiking neuron
8.2.2 PGCN learning in gridworld with a GLM spiking neuron
8.2.3 PGCN learning in mountain car
8.2.4 PGCN learning in cart pole: Comparison with Hebbian learning rule
8.2.5 Effect of modular architecture on learning performance
8.2.6 Effect of population coding on learning performance
与ANN中的连续信号传输相反，大脑中的神经元通过离散的动作脉冲相互通信。因此，传统的基于激活函数可微性假设的神经网络参数优化方法已不再适用于大脑学习过程的建模。在这个工作中，我们提出了生物学合理的反向传播替代方案，以促进SNN的训练。我们主要研究RL规则在解决时空信度分配问题中的适用性，以便在复杂任务中进行决策。在一种方法中，我们将多层神经网络中的每个神经元视为独立的RL智能体，形成特征空间的不同表征，而整个网络形成复杂策略的表征，以解决手头的任务。在另一种方法中，我们应用重参数化技巧，通过在SNN中的随机变换来保证可微。我们将这两种方法应用于传统的RL领域，如gridworld、cartpole和mountain car，并进行了比较。此外，我们还提出了一些变化和改进，以便能够在这一领域进行后续研究。
强化学习SARSA与 Sarsa(lambda)算法详解：https://blog.csdn.net/u010089444/article/details/80516345
强化学习DQN算法详解：https://blog.csdn.net/qq_30615903/article/details/80744083
大多数RL算法主要分为两类：基于价值函数的和基于策略的算法。前一类算法，如Q-Learning (Watkins and Dayan, 1992)和SARSA，将价值函数表示为从一个状态空间到一个实数价值的映射，它暗示智能体处于一个状态的好坏。另一方面，基于策略的算法如REINFORCE (Williams, 1992)将策略学习为从状态空间到动作空间的映射，它告诉智能体在每个状态下的最优动作，以使其奖励最大化。因此，这两种算法都需要解决一个问题，即学习状态空间的表征来解决手头的任务。随着任务变得越来越复杂，要学习的表征也越来越复杂。
深度神经网络是学习这些映射的一种可行方法，因为这些网络的层次结构可能会产生丰富的特征表征。用反向传播算法训练的DQN (Deep Q Network) (Mnih et al., 2015)在求解复杂RL领域方面取得了成功。这些优化技术虽然在学习特定RL任务的复杂表征方面取得了成功，但也存在一些缺点。其中一些如下：
- 与生物网络相比，深度网络需要大量的数据来优化其参数，生物网络能够使用较少的数据样本进行泛化。
- 生物网络能量效率高，而训练深度网络消耗大量能量。
- 深度网络对于对抗性攻击不鲁棒，而生物网络天生擅长处理噪声/不完整的数据，因此不易受到对抗性攻击。
在这种背景下，有必要研究生物网络中的优化过程，以深入了解人脑的功能，从而帮助设计出鲁棒的智能机器。SNN是建立在脉冲神经元上的，它仿真了大脑中神经元的大部分特征，与生物网络非常接近。
除了生物学合理性，脉冲神经元还拥有巨大的计算潜力有待利用。单个神经元脉冲模式的变异性可归因于一组丰富的因素——刺激、过去的脉冲记录、来自邻近神经元的兴奋/抑制效应。此外，在时序编码的上下文中，脉冲的精确模式(而不仅仅是其密度)存储相关信息，这个单一的计算单元能够表示复杂的特征图。在网络中加入脉冲神经元不支持传统的优化技术来训练ANN。反向传播的信度分配要求神经元的激活函数是连续可微的。由于脉冲神经元的激活函数不满足连续可微的要求，因此需要开发其他技术来优化SNN的参数，这是本工作的核心主题。
在本工作中，我们分析了两种不同的训练SNN的方法来执行RL任务，例如迷宫导航(maze navigation)和车杆平衡(cartpole balancing)。方法如下：
- 我们在(Thomas, 2011)研究的基础上，提出了一个多智能体框架，其中每个脉冲神经元扮演一个独立的RL智能体，该智能体优化其发放策略，使其获得的奖励最大化。网络中的每个神经元利用来自邻近神经元的局部信息和来自环境的全局奖励来更新其策略参数。
- 我们假设每个脉冲神经元从一个发放策略中采样其动作，从而在网络中形成一个随机节点。我们使用重参数化技巧，通过随机节点保证可微，从而实现通过网络的反向传播。
我们推导了上述方法的学习规则，并将其应用于多层SNN中的参数优化，以解决gridworld、cartpole和mountain car问题。在第1到6节中，我们讨论了基于生物学合理性约束的多智能体actor-critic框架。第7节讨论了重参数化技巧以及如何使用反向传播来训练SNN。在第8节中，我们描述了为验证我们的主张而研究的几个案例。我们将在第9节讨论这些发现并得出结论。
1 Reinforcement learning with a network of spiking agents
神经科学理论(Schultz, Dayan and Montague, 1997)指出，critic多巴胺能神经元的发放是对奖励预测误差的反应，这些在全局传播的强化信号被认为可以指导整个额叶皮层和基底节的actor神经元的学习。在此基础上，我们提出了一个基于策略梯度合作者网络理论(Thomas, 2011)的多智能体actor-critic框架。在这个框架中，我们让多层神经网络描述一个复杂的策略来解决给定的RL任务，其中网络中的每个神经元充当一个独立的RL智能体，其策略形成部分状态空间的表征。高层神经元利用下层神经元的表征形成更复杂的状态空间表征，同时保证了学习算法和信息传输的严格局部性，从而满足了生物学合理性约束。
神经元作为优化其活动以获得最大奖励的实体的概念可以追溯到享乐主义神经元的形成(Klopf, 1982)。类似的公式(Barto, Sutton and Brouwer, 1981)引入了一种称为关联搜索网络的联想记忆系统，该系统包含类似神经元的自适应元素和预测器，其中预测器向独立优化其参数的每个自适应元素发送奖励信号。(Seung, 2003)定义了享乐主义突触，其中神经元之间的连接是根据化学突触传递建模的。突触释放小泡成功或失败的概率受全局奖励的调节。
2.0.2 Learning by reinforcement in spiking neural networks
(Florian, 2007)将RL算法应用于脉冲神经元的随机脉冲响应模型(SRM)，导出了奖励调节脉冲时序依赖学习的学习规则。(Xie and Seung, 2004)提出了一种将带噪IF神经元网络中的不规则脉冲与全局奖励相关的学习规则，并证明了它对期望奖励具有随机梯度下降。(Rosenfeld, Simeone and Rajendran, 2018)采用了神经元的GLM模型，该模型具有初次脉冲编码，以学习神经形态控制的策略。
(Chang, Ho and Kaelbling, N.d.)使用全局奖励信号训练多个RL智能体，其中每个智能体将不可见智能体的贡献建模为可通过kalman滤波估计的加性噪声过程。
3 Background, Preliminaries and Notation
一个表示为马尔可夫决策过程(Markov Decision Process, MDP)的RL域由状态空间S、动作空间A、状态转移矩阵P：S × A → S和一个奖励函数R：S × A → R定义。策略是状态空间条件下的动作概率分布，定义为π(s, a, θ) = Pr(At = a|St = s)其中θ表示策略的参数。策略π的状态价值函数定义为期望奖励，Vπ(s) = E[G|S0=s, π]，其中γ是折扣因子，
是折扣奖励。
蒙特卡洛学习与时序差分学习：https://blog.csdn.net/liweibin1994/article/details/79111536
资格迹：https://blog.csdn.net/qq_25037903/article/details/82756629
时序差分学习(TD)算法通过学习状态价值函数
来评估策略π。TD(0)算法根据的两个连续预测(TD误差)的差异更新其参数θ。TD误差被定义为
。TD(0)更新由
给出。TD(λ)是TD(0)算法的扩展，其中当前奖励之前的所有状态的贡献按资格
进行加权，并进行更新
。
Policy Gradient：https://zhuanlan.zhihu.com/p/21725498
REINFORCE & Actor-Critic & PPO：https://blog.csdn.net/Pony017/article/details/81146374
3.2 Policy gradient algorithms
策略梯度算法通过函数近似将策略描述为从状态空间到动作空间的复杂映射。通过降低期望折扣奖励的梯度，
，其中
，以估计策略的最优参数。在REINFORCE中，梯度值
被估计为
。通过合并状态价值函数的估计作为基准，可以减轻REINFORCE算法所表现出的高方差。带基准的梯度
。
actor-critic属于策略梯度算法的一类，策略和状态价值函数分别由actor和critic并行学习。actor-critic中的梯度用一步奖励
代替了REINFORCE中的Gt，形成了更新公式：
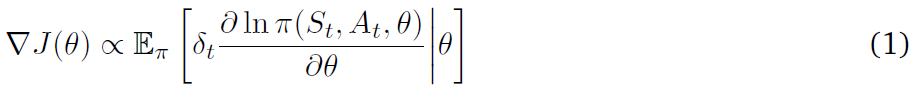
其中
是TD误差。critic使用TD算法估计状态价值函数。虽然优势actor-critic方法通过对期望折扣奖励进行梯度下降来估计状态价值函数。
3.4 Conjugate Markov Decision Processes
(Thomas and Barto, 2011)开发了一个多智能体学习框架，其中一组合作者致力于识别特征空间中的底层结构，该结构将被智能体用于解决原始MDP。因此，识别从状态空间到动作空间的映射的问题可以分解为子任务，子任务可以委托给每个合作者。这些子任务中的每一个都可以被建模为MDP，因此称为共轭马尔科夫决策过程(conjugate markov decision processes, CoMDP)。设S为原始MDP的状态空间。每个合作者的状态空间Sc是S的一个子集，其动作空间是Ac。智能体的状态空间SA = {S, Ac1 …, Acn}现在被扩展为包括合作者的动作空间，智能体的动作空间A是原始MDP的动作空间。设θ = (θA, θc1, …, θcn)为MDP的参数，其中θA为智能体的参数，θci为合作者 i 的参数。在这样的公式中可以表明，从整体上降低MDP的策略梯度等同于分别降低每个CoMDP的策略梯度。
因此，合作者理论的主要结论可以概括为：在一个合作者网络中，分别优化每个合作者的策略相当于优化整个MDP的策略。
3.5 Policy Gradient Coagent Networks
(Thomas, 2011)引入了一类actor-critic算法来优化模块化合作者网络在解决RL任务时的性能。该合作者网络称为策略梯度合作者网络(policy gradient coagent network, PGCN)，由一组合作者组成，每一个合作者通过降低由全局critic传递的TD误差所调节的局部策略梯度来优化自己的策略。这让人想起多巴胺能神经元向一群神经元发送奖励信号，以调节它们的突触可塑性(Schultz, Daya and Montague, 1997)。
考虑图1中所示的PGCN。合作者c的策略被定义为πc(Sc, Ac, θc)。每个合作者执行其策略πc，智能体A考虑合作者的动作并执行其策略πa(Sa, A, θa)，即MDP在该时刻的动作。全局critic，评估环境中的动作，并返回TD误差δ，然后将其传递给每个合作者。然后，根据等式(1)，合作者c用随机梯度下降法优化其参数，如下所示：
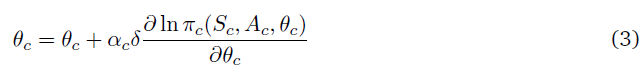
全局critic C使用相同的TD误差，使用TD(λ)算法更新其状态价值函数的估计。因此，这一合作者框架有助于建立一个生物学合理的学习规则。脉冲神经元可以被建模为合作者，其随机发放模式可以被定义为其策略。我们现在继续描述脉冲神经元的数学模型，它可以被建模为一个合作者。
4 Designing the neural agent: spiking neuron models
体内神经元的脉冲序列高度不规则，在相同的恒定刺激下不可重复。神经元脉冲序列的这种变异性被认为有利于学习。(Maass, 1996)表明，带噪SNN可以实时仿真任何McCulloch-Pitts神经元/多层感知器的函数。脉冲过程的不可靠性使得神经元可以被建模为RL智能体。
4.1 Memoryless Ising model of spiking neuron
在本节中，我们考虑了一个基于能量的脉冲神经元群发放活动模型(Ising) (Tkacik et al., 2010a)。假设一个由N个神经元组成的网络，其脉冲序列被离散化到宽度为Δt的容器中，其中对于任何神经元 i，如果该神经元在时间容器 t 发放，则σi(t) = 1； 当该神经元不活动时，σi(t) = -1。因此，在任何时刻t，网络活动的N-bit表示由神经元群的发放模式形成。脉冲活动的联合概率分布由下面给出的Boltzmann分布给出：
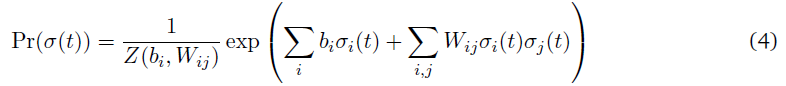
其中Z(bi, Wij)是划分函数。给定相邻神经元的活动，单个神经元出现脉冲的条件概率由下式给出：
其中
。
因此，神经元的发放策略由上述条件概率定义，参数为神经元的固有发放倾向bi和与相邻神经元的突触连接强度Wij。这种表示形式类似于限制Boltzmann机(RBM)。RBM采用对比发散算法作为学习规则来更新参数，不过本文提出了利用RL更新来调整突触权重。这种脉冲神经元的形式被定义为RL智能体，其中智能体可用的一组动作是发放(a = 1)或不发放(a = -1)。神经元的策略由π(s, a) = Pr(at = a|st = s) = Pr(σi = 1|s)定义。
进一步区分的神经元脉冲活动可以被纳入策略，而不仅仅是发放/沉默。如果动作a = 0表示位于平均发放率的发放，a = 1，a = 2表示高于平均活动一、二个标准差，其中a = -1，a = -2表示低于平均水平的发放。然后神经元的策略可以表示为
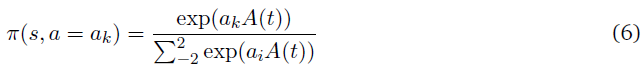
其中
。这种形式的参数化可以用来分类表示脉冲神经元的发放活动。
4.1.1 PGCN update emulates Hebbian/Anti-Hebbian learning in Ising model of spiking neurons
证明：神经元的脉冲序列被离散化到持续时间为Δt的小时间容器。然后xi(t) ＝ 1表示神经元的发放，xi(t) ＝ -1表示沉默。神经元网络发放模式的联合概率由Ising模型近似(Tkacik et al., 2010b)。当刺激/输入模式固定时，与前一层K个神经元相连的神经元的发放概率由下式给出：
根据策略梯度定理，权重更新由下式给出：
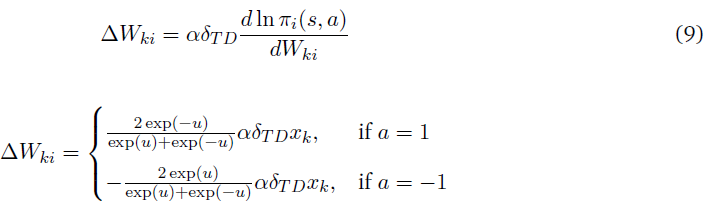
从上面的等式可以看出，当δTD>0时，权重更新遵循hebbian学习(如果xk = 1且a = 1，则更新为正，反之亦然)，当δTD<0时，权重更新遵循anti-hebbian学习。
4.2 Stochastic Leaky Integrate & Fire Neuron
在这一节中，我们考虑了一个脉冲神经元模型(Gerstner and Kistler, 2002)，它在膜电位中保持了对过去输入的衰退记忆。
假设一个突触后神经元通过它们各自的突触连接接收来自多个突触前神经元的输入。突触前神经元在任何时刻的脉冲序列所引起的突触后神经元膜电位由下列方程给出：
其中b是神经元对发放的偏差，Wk是对突触前(输入)神经元k的突触权重，zi是由于在突触前神经元k的时间ti出现脉冲 i 而在神经元中引起的突触后动作电位。
4.2.1 PGCN update emulates STDP learning in Leaky-Integrate-Fire model of spiking neurons
证明：在这里，我们考虑初次脉冲神经编码。我们假设相关信息是以神经元的模式编码的，神经元在一组神经元中首先发放。考虑三个相互侧向抑制的脉冲智能体。当其中一个发放时，三个智能体的事件都结束了。
神经元在任何时刻发放的概率(策略)由下式给出：
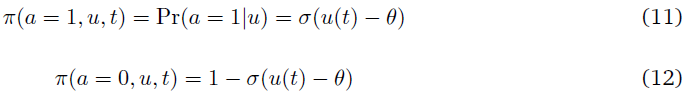
当其中一个神经元发放时，这三个神经元的事件都结束了，评论者给出的TD误差为δTD。
权重更新由以下策略梯度方程给出：
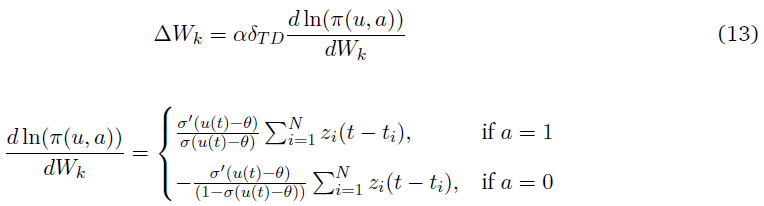
在一个LIF神经元中，突触前神经元中的一个脉冲所诱发的突触后电位从脉冲时间开始呈指数衰减：
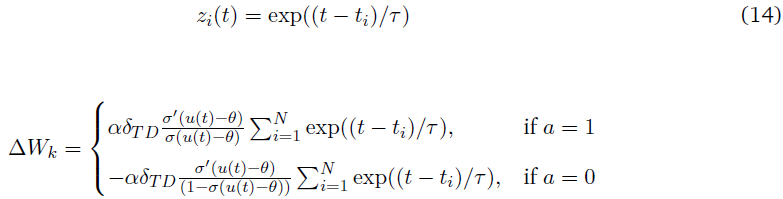
以上的更新让人想起了STDP学习规则，其突触更新依赖于突触前和突触后脉冲的相对时间。在时间 t 发放的神经元将有一个正的更新，而未能发放的神经元将有一个负的更新。抑制在这里没有被明确地建模，因为它被视为一个信号，结束了这一事件。
4.3 Generalized Linear Model of a Spiking Neuron
脉冲神经元的广义线性模型(GLM) (Pillow et al., 2008; Truccolo et al., 2005)是一个计算简单的框架，用于捕捉神经元脉冲模式与其感觉/刺激表现和邻近神经元活动的时空相关性。在这个模型中，神经元的发放活动由一组线性滤波器参数化，每个滤波器都将脉冲序列的变异性归因于一个生物学合理的现象。刺激滤波器或时空感受野，类似于卷积神经网络中的滤波器，将刺激转换成相关的高维表征。脉冲后滤波器反映了脉冲的不稳定性和爆发等历史动态对神经元当前发放活动的影响。耦合滤波器捕捉邻近神经元的抑制/兴奋性发放活动。GLM脉冲神经元的图示如图2所示(Weber and Pillow, 2016)。
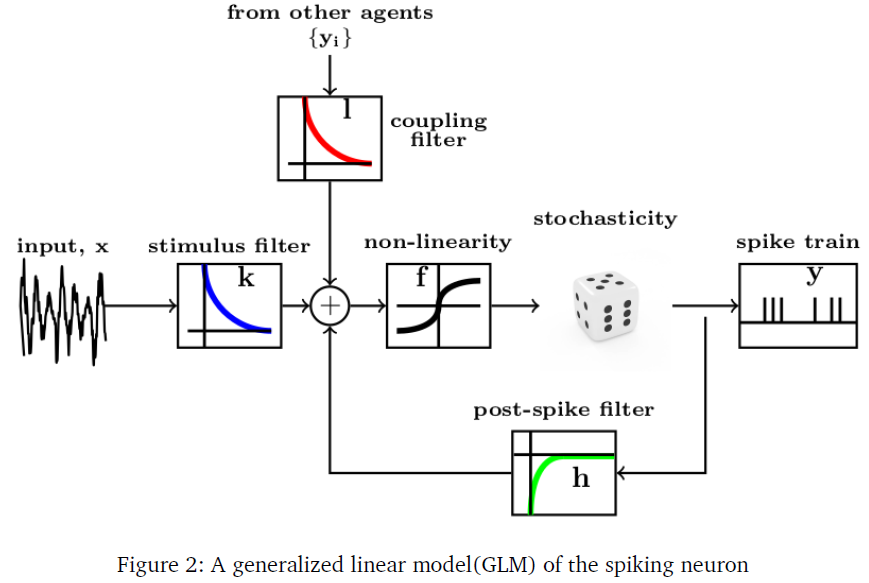
假设神经元在给定时间 t 的条件脉冲活动是从一个指数族分布中采样的，其期望值λ(t)通过一个链接函数 f 与其滤波器响应的线性组合相关 —— k (刺激滤波器)、h (脉冲后滤波器)、{li} (耦合滤波器)及其基准发放率η。
其中x是时空刺激模式，ζ是神经元的脉冲历史，ξi是第 i 个相邻神经元的发放活动。这里 f 是可逆函数。如果f-1是指数函数，则λ(t)可以表示条件脉冲发放率，而如果f-1是sigmoidal，则λ(t)可以表示任何时刻的发放条件概率。在体内观察到的脉冲序列的随机性由图2所示的随机脉冲模块来解释，该模块可以包含泊松/伯努利随机性，取决于λ(t)表示瞬时发放率还是发放概率。
上述模型的最优参数(θ* = (k, h, {li}))可以通过观察神经元的脉冲序列响应的最大似然来估计。θ*可以通过计算观测给定脉冲序列响应的对数似然的梯度和hessian来估计。
在本研究中，我们在以瞬时发放率/发放概率为策略，以GLM滤波器组为策略参数的PGCN框架下，将GLM脉冲神经元作为合作者。脉冲合作者可以通过降低与参数相关的策略梯度来优化其策略参数。我们现在讨论所提出的学习规则，以训练一个脉冲合作者网络来解决RL任务。
4.4 Linear-nonlinear-Poisson cascade neuron model
带GLM神经元模型的脉冲合作者将其脉冲策略归因于一组丰富的因素——刺激、脉冲历史、与相邻合作者的交互。该模型的一个明显简化是通过将GLM神经元模型简化为Linear-nonlinear-Poisson级联神经元模型来限制因素集，该模型可以描述如下方程：
式中，λ(t)为条件发放率，k为刺激滤波器，y(t)为合作者的脉冲序列响应。该公式适用于需要使用发放率编码而不是时序编码来编码合作者的响应的情况。神经元的动作，即瞬时发放率，可以用一个均值为λ(t)的高斯策略来执行，具体如下所示：
因此，连续策略表示可以扩展合作者以采取连续的动作，而不是离散的脉冲。通过用伯努利采样代替泊松采样，我们可以进一步简化模型，将合作者的动作减少到单个脉冲而不是脉冲序列。现在策略可以用下式来表示：
对于上述策略，合作者的权重更新如下：
在单脉冲的情况下，更新规则与Hebbian学习非常相似，从等式(15)可以看出，如果x和y具有相同的符号，则参数增加，反之亦然。
5 PGCN learning rule for a network of GLM spiking agents
考虑在一个RL域中用一个由GLM脉冲合作者组成的深度网络中的复杂状态-动作表征。我们现在描述如何在PGCN框架下，使用脉冲合作者网络来表示策略，以解决RL任务，并推导出相应的学习规则来更新策略参数。
我们将首先从时空脉冲模式的角度讨论状态空间的编码。每个状态可以用二元值(1/-1)的S×K向量表示，其中S是空间因素，K是时间因素。这里S可以解释为编码刺激的神经元数量，K可以解释为每个S神经元的脉冲序列长度(以离散时间容器测量)。任何复杂的状态表征都可以通过转换成时空模式进行编码。如果状态包含灰度/彩色图像，则状态可以用瞬时发放率(而不是发放概率)来表示。然而在本研究中，我们主要将脉冲序列视为一系列二元脉冲。在扩展中，我们讨论了如何处理脉冲序列作为一系列瞬时发放率。
状态神经元形成深度合作者网络的第一层，这是对第一个合作者层的刺激。网络的其余部分是分层组织的，其中一层合作者的脉冲序列响应形成了对下一层合作者的刺激。如前一节所述，同一层内的合作者与兴奋性/抑制性效应具有耦合连接。
考虑网络的层(n)中的脉冲合作者C。设xt = (x(0), …, x(S))为合作者C的刺激，其中
为前一层(n-1)的第 i 个合作者的时序脉冲响应模式。设ζt = (y0, …, yt-1)为合作者的脉冲历史向量。设
为前一时刻同一层神经元的发放活动，假设相邻神经元的兴奋性/抑制性活动在下一时刻启动，从而避免更新中的重复。合作者C的状态空间由元组(xt, ζt, ξt-1)给出。合作者在 t 时刻的条件发放概率由下式给出：
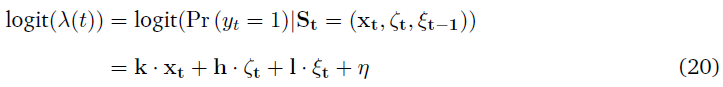
式中，k，h，l是合作者C的滤波器，等式(1)中的链接函数 f 被选为logit函数，其中
(logit与sigmoid互逆)。
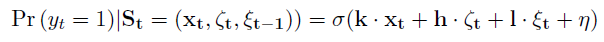
其中σ是sigmoid/logistic函数。
考虑一个MDP时间步骤。在该时间步骤中观察到脉冲序列y的条件概率由下式给出：
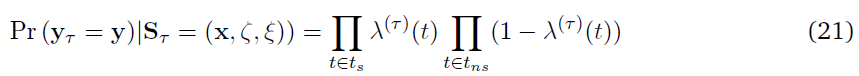
式中，λ(t) = σ(k · xt + h · ζt + l · ξt + η)，τ是MDP尺度上的时间。ts表示脉冲出现的时间，tns表示没有脉冲的时间。(x, ζ, ξ)表示在MDP时间尺度上表达的完整时空脉冲模式。等式(7)表示合作者c的策略参数化，πc(s, a, θ)，其中它的扩展动作是脉冲序列响应ac = y，状态空间sc是元组sc = (xt, ζt, ξt-1)和参数向量θc = (k, h, l)。
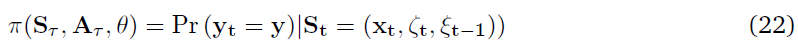
策略的对数概率由下式给出：
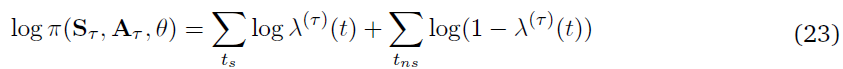
对数发放概率的向量λ = (λ(0), …, λ(t))可以通过对带滤波核的刺激向量进行卷积来计算。
根据等式(3)，合作者c的每个策略参数的更新公式如下：
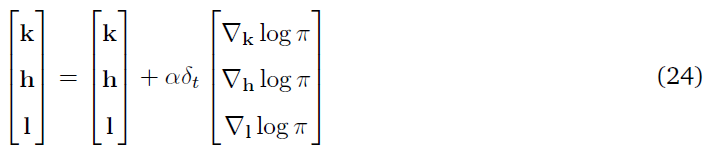
式中，δt是由全局TD(λ)评论者传递的TD误差，并且
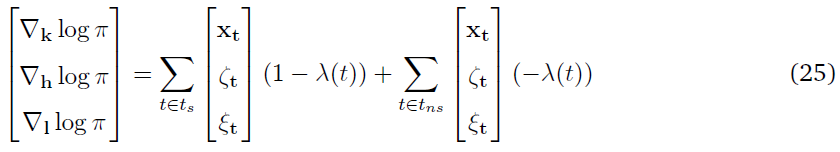
等式(9)也是观测到脉冲合作者中给定脉冲序列响应的对数似然。通过等式(10)中的更新，我们增加了脉冲序列导致正TD误差的概率，并降低了导致负TD误差的概率。因此，每个合作者都在接收到全局误差的上下文中独立地更新其脉冲策略。在简单版的合作者网络中，每一个合作者网络都会进行更新，就好像它的脉冲策略会导致MDP迭代中网络的动作选择一样，这并不一定。这将导致权重更新的高方差。在讨论这个问题之前，我们讨论了上述模型的一些简化和扩展。
在这一部分中，我们比较了在等效网络中，合作者学习规则和反向传播规则的均值和方差更新。GLM脉冲合作者在给定的时间间隔内输出脉冲/无脉冲的概率。如果脉冲序列时间步骤随时间展开，则可通过分别对核k、h、l在状态空间sc = (xt，ζt，ξt)上执行卷积来计算瞬时发放概率。如果直接使用这些概率来计算下一层的响应，而不是从这些概率中进行采样，我们本质上拥有一个类似于CNN的网络，并且卷积运算是可微分的，能够通过网络进行反向传播。因此，可以从合作者网络中构造有利于反向传播的等效网络。反向传播网络的策略是
其中，softmax动作选择从最终动作概率ok完成，W是网络的参数矩阵。我们现在计算核kij的期望权重更新，它是与输入神经元和第 j 个隐神经元相关的参数向量。
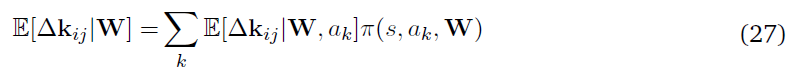
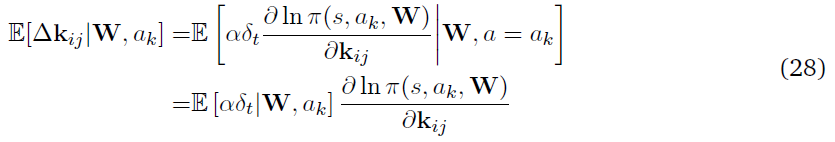
如果ol是第 l 个输出神经元，而λj(t)是神经元 j 在 t 时刻的瞬时发放概率，则该策略的对数导数可以写成：
等式(20)中括号内的项可视为 t 时刻神经元 j 的发放概率对整体动作选择的贡献。
我们现在将在脉冲合作者网络中推导出期望更新kij。给定参数向量W，kij的期望权重更新为：
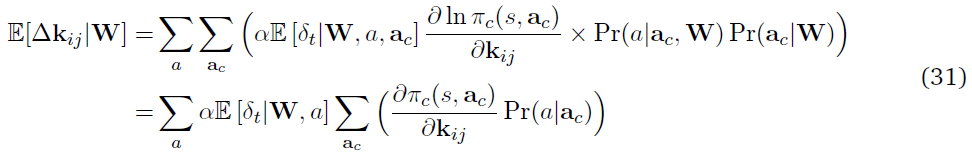
等式(21)用
的事实被简化为：
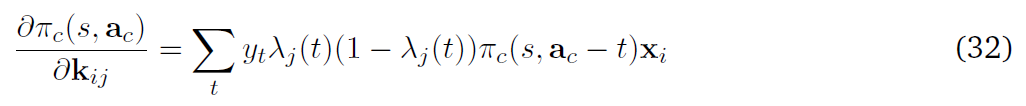
其中π(s, ac - t)表示神经元的策略，不包括其在第 t 个时间步骤的动作。
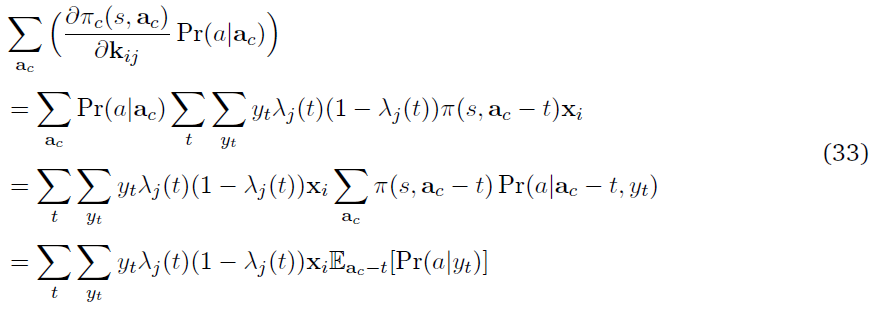
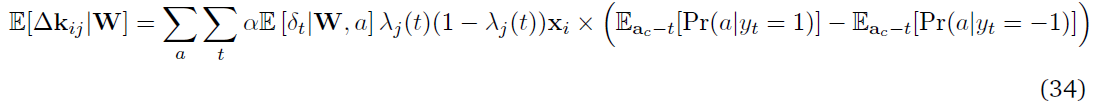
等式(24)中括号内的最后一项是决定在 t 时刻合作者的发放yt有多少可能导致网络的动作a的因素。现在将等式(24)与来自反向传播更新的对应等式(20)进行比较。这两个等式是相同的，除了括号中的项。在反向传播中，分析推导了在 t 时刻合作者发放的贡献，而在脉冲合作者中，当在多个试验中取样时，实现了相同的因素。在多个试验中平均，来自反向传播和合作者更新的期望更新大致相同。但在合作者网络的情况下，更新的方差较大。从等式(20)可以清楚地看出，对于给定的参数向量和状态，反向传播中随机性的唯一来源是MDP状态转换。但是，在合作者的情况下，一个更新有多个方差源(合作者(Eac)和网络的其他部分(Pr(a|yt))。
6 Performance enhancement through variance reduction
有多种技术可以中和合作者网络中的方差源。一种技术是更新学习规则，使其包含一个额外的因素，该因素与给定的合作者对网络动作选择的贡献相关，如AGREL (Roelfsema and Ooyen, 2005)。学习规则可以修改为
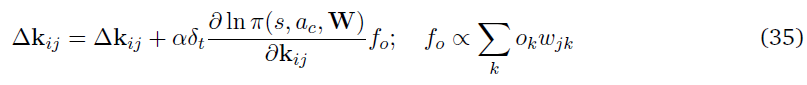
其中，fo是从输出层到合作者的反馈因素，ok是输出层中第k个合作者的活动，wjk是隐含层中合作者与输出层中合作者的相关参数。
在本文中，我们选择避免反馈因素，这些因素可能包括关于网络其余部分中权重的信息，而仅仅集中于局部更新来自网络其余部分的最小反馈。我们专注于通过仅仅针对架构设计来减少方差。
6.1 Variance reduction through a modular connectionist architecture
脑网络具有层次模块化的特点，即每个模块由子模块组成，子模块又由几个子模块组成。这种模块化结构被认为是在不断变化的刺激条件下加快系统适应和进化的原因(Meunier, Lambiotte and Bullmore, 2010)。(Jacobs, Jordan and Barto, 1991)表明，与全连接的结构相比，将任务分解为许多功能独立的任务，在神经网络中结合模块化结构可以加快学习速度。在本研究中，我们证明这种模块化结构有助于局部学习规则。
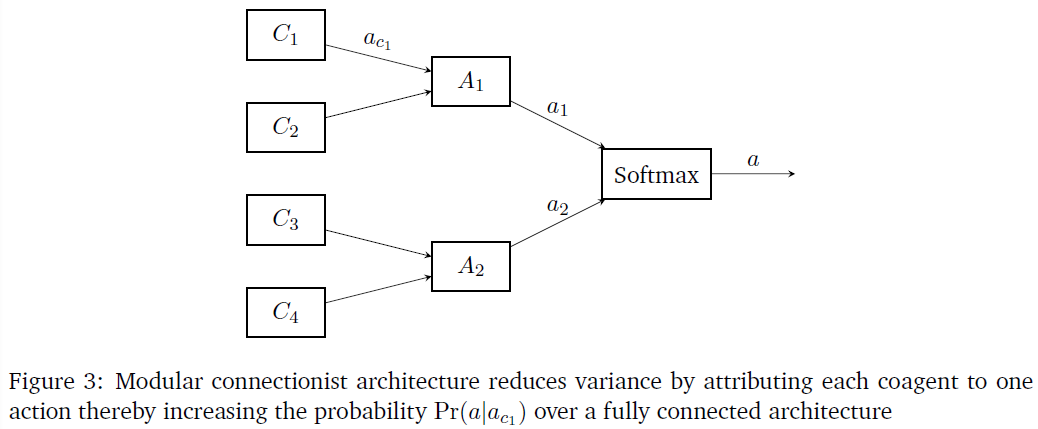
图2显示了一个模块化连接结构，该结构具有稀疏的模块化连接，而不是全连接结构。从图中可以看出，隐含层中的任何一个合作者只与输出层中的一个合作者相连。这可以扩展到多个隐含层，方法是将一个层中的合作者分解为模块，其中给定的模块仅连接到下一层中的相应模块。(Plaut and Hinton, 1987)表明，在这种模块化结构中学习比在全连接结构中学习要快得多。
在模块化网络的情况下，当在选择动作时观察到TD误差时，属于动作模块的所有层中的合作者被更新。为了提高学习速度，我们选择适当地更新属于其他动作模块的合作者。如果发放了所需的动作，则负责发放该动作的所有合作者都将受到负TD误差的惩罚。另一方面，如果动作没有被发放，则对应于该动作模块的合作者将得到一个正TD误差的奖励。这是为了确保对于任何给定的状态，只发放所需的动作，而其余的动作是静默的。因此，在MDP的任何迭代过程中，所有的合作者都会被更新。
6.2 Variance reduction through population coding
如前所述，在多个试验的平均情况下，合作者网络中的权重更新近似于权重对总体动作选择的贡献。一个明显的降低方差技术是在多个试验中平均权重更新。此平均可以通过在多个试验中运行同一个网络或并行运行多个网络并基于集成活动选择动作来完成。这种由一群神经元的联合活动动作编码的形式被称为群体编码。实验证据支持这种编码技术广泛应用于大脑的传感器和运动区域(Maunsell and Van Essen, 1983)。
我们运行一群网络，从输出神经元获得脉冲响应，然后在网络上求平均值，得出最终的输出概率。通过应用softmax函数从输出向量中选择动作。在对各个网络执行更新时，TD误差将按原样传递给网络，如果网络选择的动作与集合的最终动作相同，则TD误差将以相反的符号传递。这些更新是策略外的，因为集成执行的动作可能不是当前网络策略选择的动作。
7 Reparameterization trick in spiking neural networks
在前一章中，我们介绍了一种训练SNN的局部学习算法。然而，该算法易受高方差的影响，我们试图通过结构变化来减轻这种影响。在这一章中，我们介绍了第二种训练SNN的方法，这种方法不仅依赖于局部信息，而且与反向传播的关系更为密切。
如前所述，由于其信息传输的离散性，将反向传播算法应用于SNN是不可行的。为了克服这一障碍，我们采用变分推断中发展的技术来促进通过随机节点的反向传播：重参数化技巧(Kingma and Welling, 2013)。我们将脉冲神经元的策略建模为通过采样产生脉冲的概率分布。然后，我们应用重参数化技巧，通过样本反向传播，在单个神经元之间分配信度/责备。
重参数化技巧使我们能够将采样中的随机性建模为模型的输入，而不是将其归因于模型参数，从而使所有模型参数连续可微的，从而促进反向传播。
在这一节中，我们回顾了文献中试图应用反向传播来训练SNN的方法。(Lee, Delbruck and Pfeiffer, 2016)将脉冲神经元的膜电压电位视为可微信号，其中脉冲时间的不连续被视为噪声。这使得反向传播能够直接作用于脉冲信号和膜电位。(Huh and Sejnowski, 2017)建立了一个脉冲神经元的可微突触模型，并推导出了精确的梯度计算。(Bohte, Kok and Poutré, 2002)介绍了SpikeProp算法，其目标是在给定输入模式的情况下，学习输出神经元的一组发放时间。该算法利用误差函数进行反向传播，该误差函数为期望脉冲时间与实际脉冲时间之差的总和。类似地(Mostafa, 2016)使用一种时序编码方案，其中信息以脉冲时序而不是脉冲发放率编码，网络输入-输出关系几乎在任何地方都是可微的。在(Kheradpishh and Masquelier, 2019)中，网络使用一种称为rank-order编码的时序编码形式。在这种编码技术中，脉冲神经元仅限于每个神经元一个脉冲，但神经元之间的发放顺序携带相关信息。此文章推导出了一种类似于反向传播的算法S4NN。
据我们所知，这是第一篇运用重参数化技巧通过SNN反向传播误差的文献。
考虑以下期望，其中离散随机变量z从依赖于θ的分布pθ(z)采样，fθ(z)是损失函数。
为了找到使上述期望最小化的最佳参数θ，我们需要计算其导数
为了使上述导数对θ可微，随机变量z表示为确定性变量的可微函数，并带有如下所示的加性噪声：
其中ε是从概率分布p'(ε)中采样的加性随机变量。这里x是模型的参数，它是确定性的，因此是可微的。ε是一个噪声项，这解释了模型的随机性。(3.2)中的导数现在可以计算如下：
gΦ的选择可以是任何方便的分布，例如正态分布，但是在我们的例子中，我们选择了一个称为Gumbel-softmax的特殊函数。
7.3 Reparameterization through gumbel-softmax
脉冲神经元的动作是从一个概率与每个动作类别相关的的分类分布中采样的。从分类分布中采样通常是一个非可微函数。在(Jang, Gu and Poole, 2017)中，引入了一个Gumbel-softmax函数，它提供了一种从分类分布中提取可微样本的方法。
Gumbel softmax函数生成如下示例：
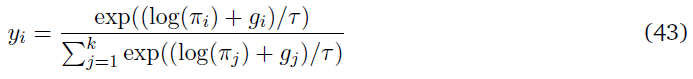
其中gi是来自Gumbel(0, 1)分布的独立同分布(iid)样本，该样本是通过从正态分布N(0, 1)中采样u并计算g(u) = -log(-log(u))生成的。上述方程从策略的动作πi的对数概率生成分类样本yi。
7.4 Spiking neuron as a stochastic node
为了应用重参数化技巧，需要将脉冲神经元建模为一个随机节点，其动作从概率分布中采样。上一章中描述的任何一个脉冲神经元模型都可以用来对神经元进行建模。作为概念的证明，我们使用了一个无记忆脉冲神经元的简单版本。
神经元的策略如下：
其中bi、Wij是策略的参数。然后使用如下所示的Gumbel-softmax函数从策略的对数概率中对层的输出进行采样：
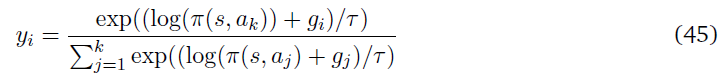
假设下一层将输出yi转换为f(yi)。关于策略参数Wij的微分可以计算如下：
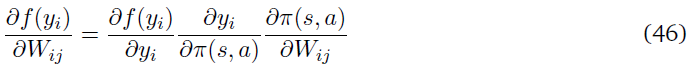
actor网络和critic网络都是共享初始层的多层神经网络。使用优势actor-critic学习技术(Mnih et al., 2016)优化网络，其中使用优势函数进行策略梯度更新。
在本节中，我们使用前面章节讨论的技术来训练SNN，并将其应用于RL的各种环境中。我们比较并对比了本研究所发展的局部学习架构与重参数化技术的反向传播。(PS：具体实验可参照OpenAI(http://gym.openai.com/envs/))
8.1 Reinforcement learning domains
本研究使用下列RL领域(包括延迟奖励和连续控制设置)。
在这个领域中，智能体必须在迷宫般的环境中导航，通过学习提供最大可能奖励的路径来达到最终状态。智能体有四个移动选项(上、下、左、右)。智能体朝指定方向移动的概率为0.8。智能体偏离预定方向右转的概率为0.05，左转的概率为0.05。智能体不执行动作的概率为0.1。如果智能体试图朝着超出域边界的方向移动或遇到障碍，则智能体将保持静止。智能体在状态1中启动，当它到达状态23时，过程结束。
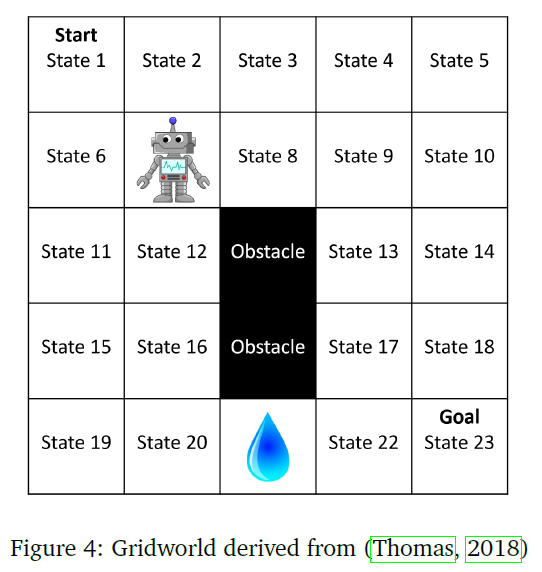
10×10的gridworld域是5×5域的扩展版本，但没有障碍。(10, 10)处的状态是奖励为10的最终状态。每一次其他转变的奖励都为零。环境具有随机动作，其中以0.8的概率执行给定的动作，智能体以0.05的概率向左偏转，以0.05的概率向右偏转，并且以0.1的概率保持在相同的位置。
cart-pole环境由两个相互作用的物体组成：一个位置为x，速度为v的小车，一个角度为θ，角速度为ω的杆。状态向量由这些连续变量(x, v, θ, ω)和(Florian, N.d.)中描述的动态组成。任务是用两个可能的动作在200个时间步骤中对杆进行平衡，并且在杆保持平衡的每一个时间步骤，奖励都为1。
在这个领域里，智能体的任务是让一辆被困在一个山谷里的小车，到达车前的山顶。智能体有三种可能的动作：前进、后退、不变。每过一个时间步骤，直到车到达山顶，奖励都是-1。
8.2.1 PGCN learning in gridworld with a memoryless spiking neuron
本研究是在5×5的gridworld任务中进行的。这23种状态用7个二元编码的输入神经元来表示，其中+1表示发放，-1表示静默。隐含层由10个神经元组成，输出层由4个神经元组成，每个神经元代表来自动作空间的不同动作。为了减少方差，10个这样的网络并行运行，并对其输出进行平均，以给出每个动作的平均发放率。然后将softmax函数应用于输出发放率以选择动作。将由此获得的学习曲线与使用如图所示的类似架构通过反向传播获得的曲线进行对比。
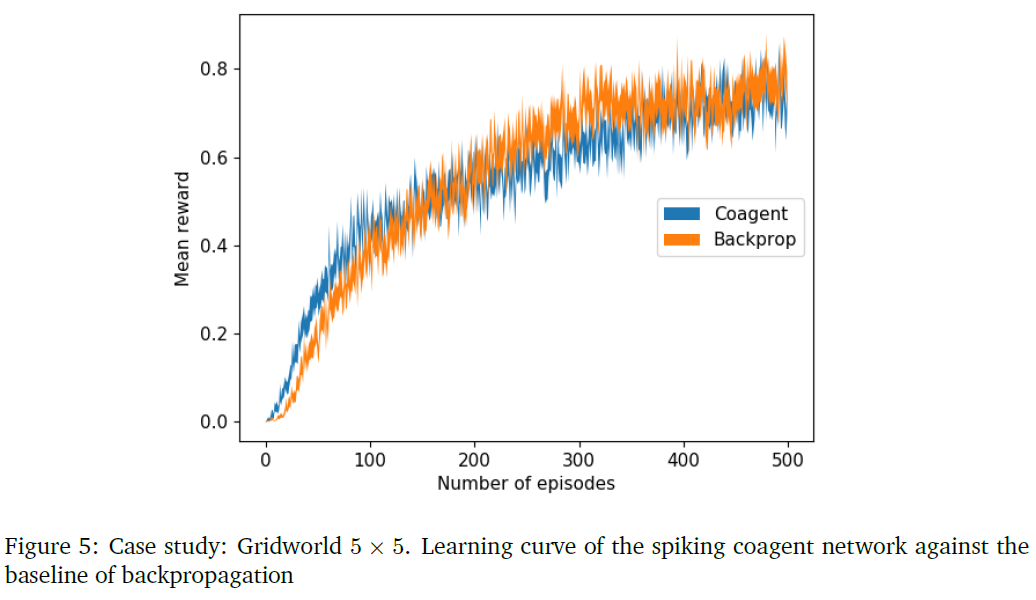
8.2.2 PGCN learning in gridworld with a GLM spiking neuron
本研究是在10×10的gridworld任务中进行的。gridworld的100个状态由3个神经元编码，其脉冲序列长度为5。隐含层有5个合作者，每个合作者的脉冲序列长度为3。合作者的刺激滤波器k是3个参数的核心，它与前一层的脉冲序列刺激卷积后产生隐含层的脉冲序列响应。为了简单起见，我们忽略了其他滤波器。输出层有4个合作者，每个合作者对应gridworld领域的动作，并且合作者的活动被编码在单个脉冲中。每个合作者的策略如等式(10)中所述。在前一节中描述的模块化连接结构中组织了合作者。同时使用10个这样的网络群来选择动作。
优势actor-critic网络用作此领域的基准。该状态的编码方式与脉冲合作者的编码方式类似，其时间分量被展平为空间分量。actor网络是一个三层网络，输入层由15个神经元组成，隐含层由100个神经元组成，输出层由4个神经元组成。critic也是一个神经网络，其结构与actor网络相同，但输出层有一个节点表示价值函数。我们还将脉冲智能体actor-critic和优势actor-critic与表格式actor-critic进行了比较，如图6所示。从图中我们可以看出，表格式actor-critic在gridworld的简单任务中工作得很好，但是脉冲智能体actor-critic在性能上接近于优势actor-critic。
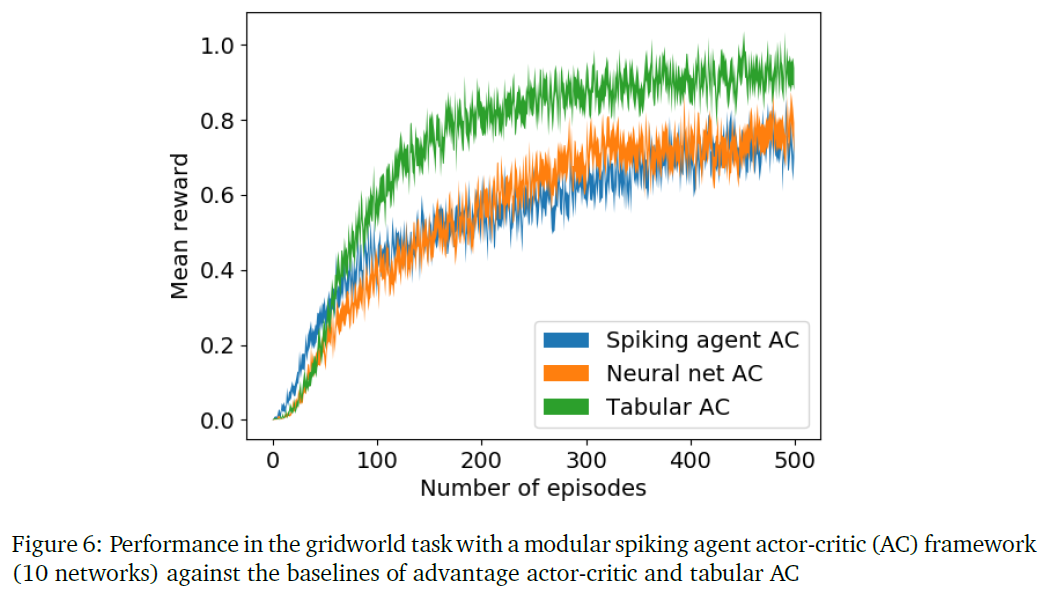
8.2.3 PGCN learning in mountain car
将无记忆脉冲神经元模型应用于mountain car任务。执行者网络是一个三层神经网络，输入层有20个神经元，隐含层有50个神经元，输出层有3个神经元。在输入层，10个神经元表示状态，其余10个神经元表示速度。连续状态变量用二元编码输入层表示。输出层负责来自动作空间的三个可能动作。这些动作是通过在10个这样的网络中平均来选择的。图7显示了在mountain car任务中完成的学习。
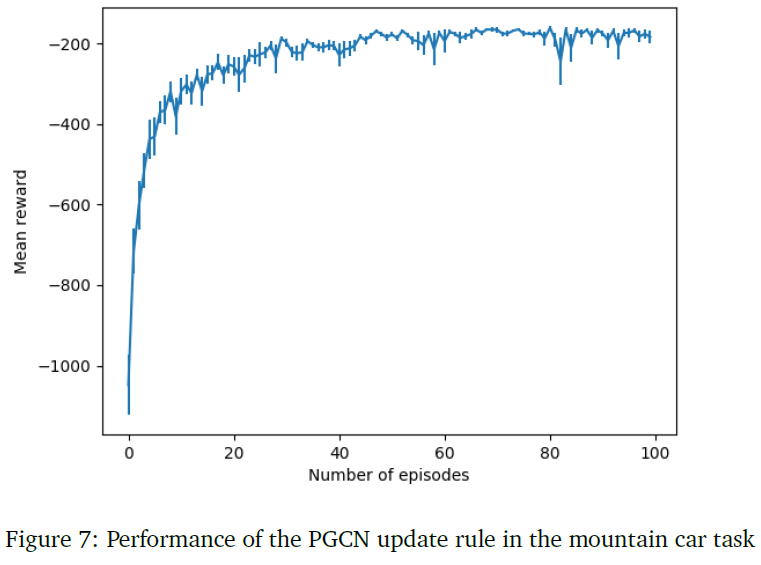
8.2.4 PGCN learning in cart pole: Comparison with Hebbian learning rule
我们现在将无记忆脉冲神经元模型应用于cartpole任务。我们使用4个输入神经元来表示4个状态变量的值。输入神经元不是脉冲性质的，而是以连续形式表示变量。隐含层有200个脉冲智能体，输出层有2个智能体代表动作空间中的两个动作。和以前一样，使用10个这样的网络群来选择动作。
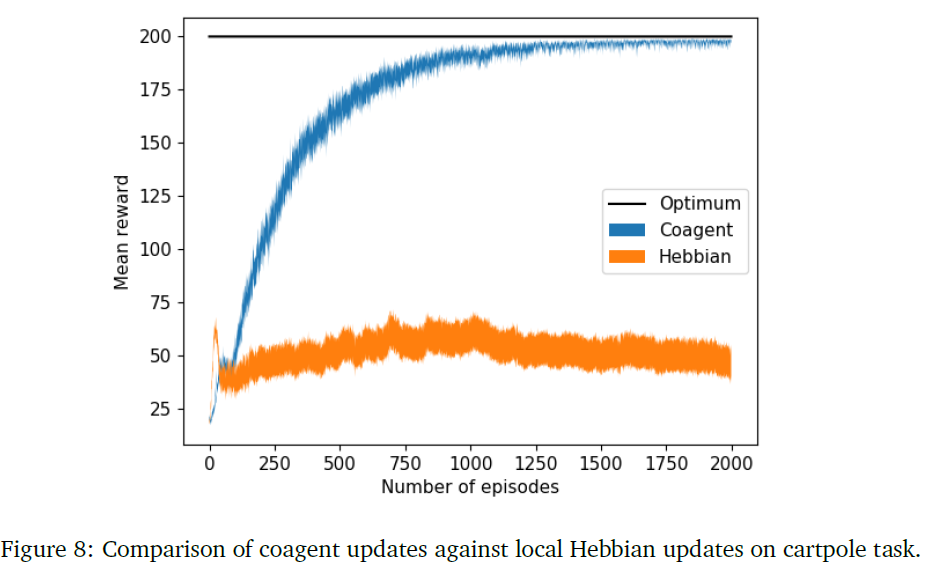
正如我们在等式(15)中看到的，单脉冲模型的权重更新等同于以梯度为因素的Hebbian更新。我们现在确定梯度因素在收敛到最优策略中的作用。在这里，我们比较了二元随机脉冲网络中的合作者策略梯度和局部Hebbian更新的性能。Hebbian规则根据下面的等式更新突触的权重：
其中xi、xj是突触前和突触后神经元的脉冲活动。
我们使用4个输入神经元来表示4个状态变量的值。隐含层有200个合作者，输出层有两个用于这两个动作的合作者。使用10个这样的网络群来选择动作。
图(5a)显示了合作者更新与简单Hebbian相关更新的比较。每个实验分别调整学习率安排和动量的超参数。可以看出，Hebbian更新导致高方差，而局部策略梯度是收敛到最优策略的关键。
8.2.5 Effect of modular architecture on learning performance
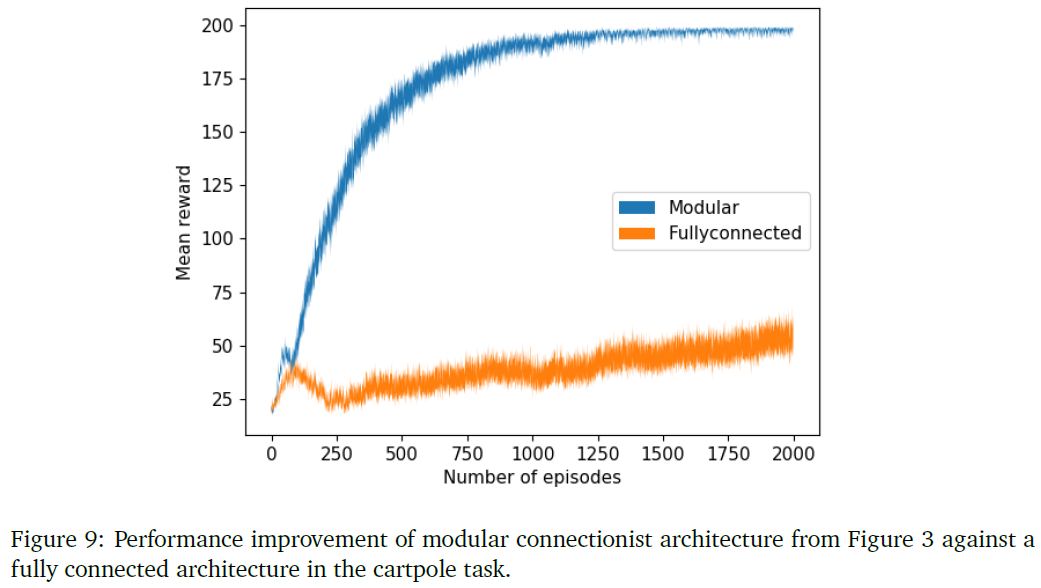
在这个实验中，我们测试了采用模块化架构所实现的cartpole的性能提升。作为概念的证明，我们在同一个任务中，首先使用全连接网络，然后使用图9中所示的模块化连接结构来训练合作者网络。所有的曲线都是通过10个网络的平均得到的。图(5b)显示了两种架构的学习曲线的比较。可以看出，全连接网络几乎无法学习策略，而模块化结构则收敛到最优策略。
8.2.6 Effect of population coding on learning performance
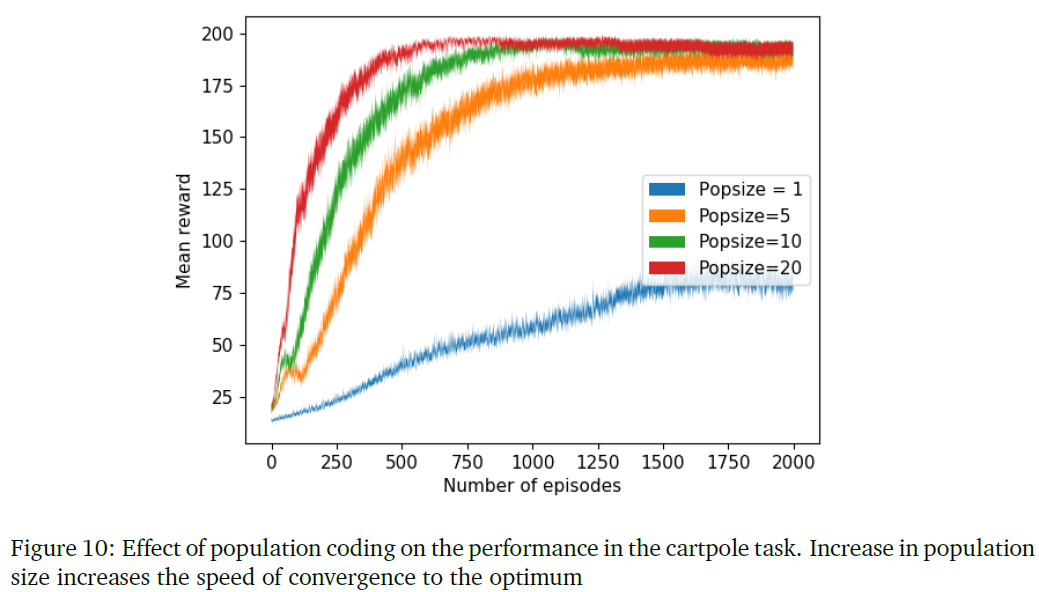
在这个实验中，我们证明了群体编码作为一种降低方差技术的有效性。通过对不同数量的网络求平均，将合作者网络应用于cartpole任务。我们首先通过使用一个网络得到一个学习曲线，然后逐步增加群体规模，以说明增加群体规模如何减少学习中的方差并提高其解决任务的性能。我们对所有设置使用模块化架构。图10显示了通过在步骤1、5、10和20中增加群体大小而实现的性能改进。
上述实验的代码可以在https://github.com/asneha213/spiking-agent-RL中被发现。
在这项研究中，我们介绍了两种训练SNN以执行RL任务的技术。在第一种技术中，我们扩展了享乐主义神经元(Klopf, 1982)，(Seung, 2003)的概念，将脉冲神经元作为RL智能体。我们探索了各种脉冲神经元的模型，以便将神经元作为RL智能体进行有效的建模。广义线性模型在计算上是可处理的，它能很好地模拟生物神经元的大多数特征。我们还使用了一个无记忆的脉冲神经元模型作为概念证明来验证我们的一些观点。尽管我们的学习框架是一种强大的表示技术，但它的收敛性具有高方差，这在所有的局部学习范式中都是不可避免的。为了缓解这个问题，我们分析了我们的更新相对于来自等效网络的反向传播更新的均值和方差。在分析的基础上，我们更新了我们的框架，与传统的优化技术相比，我们采用了降低方差技术来确保竞争性能。在不同的技术中，我们将脉冲神经元建模为一个随机节点，从概率分布中采样动作，并利用变分推断的重参数化技巧通过SNN进行反向传播。
在这项研究中，我们使用没有任何循环连接的前馈网络。(Kostas, Nota and Thomas, 2019)扩展了PGCN框架，以在出现循环连接时考虑异步更新。将这项工作扩展到包含循环抑制性连接是一个可能的未来方向。(Maass, 1997)理论上证明了时序编码的带噪脉冲神经元比sigmoidal神经元具有更大的计算能力。开发架构和学习规则来利用这种计算能力可能会对AI的发展产生影响，同时也会对人脑的功能产生影响。