郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！
CogSci, (2013)
Abstract
我们提出了一个基于生物学的神经模型，能够在复杂的任务中执行RL。该模型的独特之处在于，它能够在一个动作、状态转换和奖励之间存在未知且可变的时间延迟的环境中，解决需要智能体执行一系列未得到奖励的动作以达到目标的任务。具体来说，这是第一个能够在半马尔可夫决策过程(Semi-Markov Decision Process, SMDP)框架内发挥作用的RL神经模型。我们认为，当前建模工作的这种扩展为人类决策的日益复杂的模型奠定了基础。
Keywords: 强化学习；神经模型；SMDP
1. Introduction
RL是计算建模与大脑研究交叉融合的最成功领域之一。这始于Schultz (1998)的工作，他证明了模型的明确的计算机制(例如TD (Temporal Difference, 时序差分) RL)可以洞察大脑中一些更不透明的机制(例如多巴胺信号)。
早期研究中使用的模型是纯粹算法的，与大脑的生物学特性关系不大。然而，自第一次论证以来，许多新的模型已经开发出来，允许与神经机制进行新颖或更详细的比较。这些神经机制对应的模型更接近反映大脑结构(Frank & Badre, 2012; Stewart et al., 2012)、单个神经元的行为(Seung, 2003; Potjans et al., 2009)或突触学习机制(Florian, 2007; Baras & Meir, 2007)。
在我们的工作中，我们试图保留这些模型的神经解剖学细节，并对它们的功能进行拓展，即建立能够进行更强大的学习和决策的模型，使它们能够解决更复杂的问题。在此，我们将介绍一些这个方向的初步工作。具体来说，我们将讨论实现并展示一个模型的早期结果，该模型能够解决需要扩展动作序列的任务，在这些环境中，动作和奖励之间可能存在未知且可变的时间延迟。
强化学习中的蒙特卡罗学习以及TD学习：
https://blog.csdn.net/liweibin1994/article/details/79111536
2. Background
Sutton & Barto对RL的开创性介绍说明了扩展神经RL模型功能的重要挑战：“强化学习是学习如何将状态映射到动作，从而最大化数字奖励信号……在最有趣和最具挑战性的情况下，动作不仅可能影响即时奖励，也可能影响后续的状态，并通过这种状态，影响所有随后的奖励(Sutton & Barto, 1998)。”
大多数现有的神经模型只进行联想强化学习(associative RL)，而不考虑未来的奖励(Niv et al., 2002; Seung, 2003；Baras & Meir, 2007; Florian, 2007; Izhikevich, 2007; Frank & Badre, 2012; Stewart et al., 2012)。这类任务的一个例子是bandit学习，智能体选择n个可用选项中的一个，接收奖励，然后重置回选择点。每个试验都是独立的，因此智能体只需要了解与每个选项相关的即时奖励，然后选择最优的一个。这可以用RL符号表示为下式：
其中Q(s, a)是智能体对在状态s采取动作a的价值估计，r(s, a)是在该状态采取动作所收到的即时奖励。这些Q值可以通过观察r(s, a)，然后更新Q(s, a)，使其更接近观测价值来进行学习。上述许多模型所面临的挑战是如何以一种神经学合理的方式进行更新。
一个更复杂的RL任务的例子是导航问题，其中寻求达到目标的智能体必须选择移动的方向。智能体做出选择可能不会得到即时奖励，但仍然有好的和坏的选择(使其更接近或更远离目标)。为了做出正确的决定，智能体不仅需要知道即时奖励，而且还需要知道在采取某一动作后的期望奖励。这可以表示为下式：
换言之，采取动作a的价值等于即时奖励(如前一种情况)，加上在结果状态下采取动作的期望价值(表示该状态下期望未来奖励)。未来价值的折扣γ<1，表示未来奖励价值低于即时奖励。在到达状态s'时，通过将动作a的期望价值与观测价值进行比较，可以学习Q值。这是TD学习公式(更具体地说，这是Sarsa学习更新(Rummery & Niranjan, 1994))：
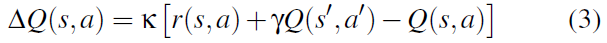
大脑所面临的这类最复杂的问题需要考虑某一特定动作的未来影响；因此，建立能够进行这类学习的模型是理解大脑决策过程的重要一步。
Sarsa和Q-learning算法对比：
https://blog.csdn.net/qq_39388410/article/details/88795124
目前已经建立了一些模型来解决这些类型的任务，但它们通常采用给定的TD误差信号(等式3)，或者在模型之外进行计算(Foster et al., 2000; Strösslin & Gerstner,, 2003)。这就简化为一个与等式1非常相似的问题。在等式1中，智能体有一个信号进来，只需要担心该信号的当前值。TD学习的挑战性在于如何在只有即时奖励作为模型输入的前提下进行学习。
Potjans et al. (2009)提出了RL最完整的神经模型之一。为了计算TD误差，他们在代表Q值的神经元输出上使用了两条活动迹，一条是快的，一条是慢的。在系统从状态s转换到状态s'后的一个短暂的时间窗口内，慢迹仍表示Q(s, a)，而快迹表示Q(s', a')；将该信息与传入的奖励相结合，使神经元能够计算等式3的等效值。
这种方法的缺点是，只有在状态转换之后，并且在慢活动迹赶上快活动迹之前的时间窗口内，才会立即提交必要的信息；如果动作选择发生在状态转换之前，或者如果奖励没有在该窗口内传递，系统将无法学习。所有依赖某种类型的活动/资格迹来保存动作价值的系统都是如此(例如，Izhikevich, 2007; Florian, 2007)。这些模型依赖的环境，遵循可靠的类似时钟的序列，包含动作选择、状态转换和奖励。
在某些情况下，这可能是一个合理的假设，但在我们的工作中，我们寻求一个更一般的机制，在动作选择和状态转换或奖励之间存在未知且潜在可变的延迟时，它可以进行学习。这可以表示为半马尔可夫决策过程(Semi-Markov Decision Process, SMDP; Howard, 1971)。在基本MDP (RL任务的标准模型)中，状态、动作和奖励都是瞬间发生的，而SMDP引入了动作选择和状态转换之间的时间延迟的概念，并且奖励可以在不同的时间点传递。
解决MDP环境中的时间延迟问题的一种方法(不使用SMDP)是将延迟周期想象为一系列状态转换。也就是说，状态/动作/奖励继续以常规的类似时钟的方式进行，并且时间延迟通过该循环的多个周期来表示。然而，这需要学习通过延迟期间所做的所有"决定"进行传播。这使学习过程变得非常复杂，而且对于许多不同决策的长延迟期，这会使成功的学习变得几乎不可能。SMDP框架的一个重要优点是，它将延迟期的所有活动封装在一次学习更新中。这在诸如层次决策等情况下特别有用，在结论中我们将进行更多的讨论。
等式3中的学习更新可以针对SMDP环境(Bradtke & Duff, 1994; Sutton et al., 1999)重新改为下式：
其中 t 是自选择动作a以来经过的时间，r(s, a, t)是在 t 时刻接收到的奖励，并且在τ时刻发生到状态s'的转换。明显的变化是 a）随时间累积的接收到的奖励，b）在整个延迟期间应用折扣。然而，更微妙的变化是，智能体不知道τ，也就是说，它不能依赖于奖励，或者折扣被限制在某个特定的时间窗口内，或者在特定的时间应用更新；它必须简单地等待，并且能够在状态变化发生时计算等式4。为了简单起见，我们在这里将时间表示为由离散时间步骤组成的，但它可以通过对传入的奖励信号进行累加(这是我们模型中使用的方法)在连续情况下进行表示。
使用SMDP框架，智能体可以学习在更一般的环境中选择动作，并将任意时间延迟纳入RL过程。通过将这一理论应用到神经模型中，我们将开发一个更强大、更灵活的大脑RL模型。
3. Methods
3.1 Model architecture
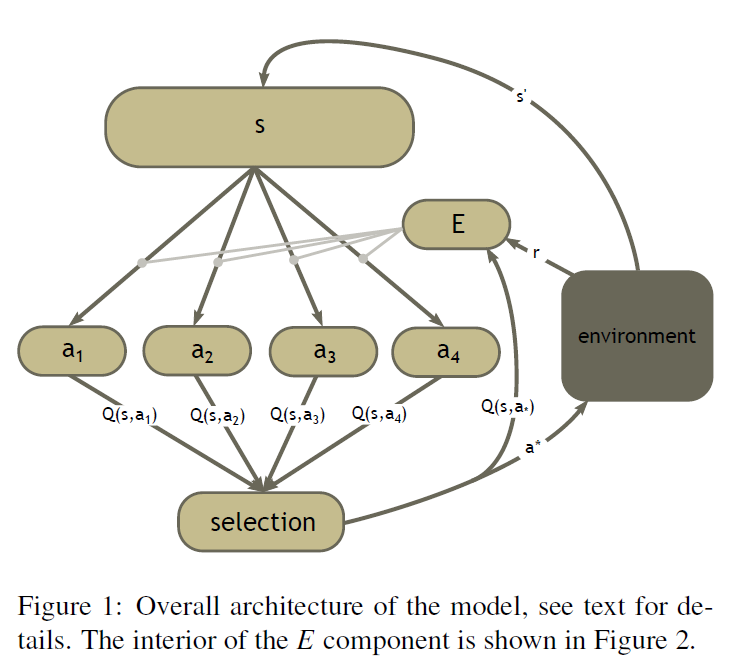
模型的总体结构如图1所示。顶部是代表当前状态的神经元群体(我们将在下一节讨论如何将环境状态转化为神经活动)。下面是与每个可用动作相关联的群体(在本例中为4个，但模型可以处理任意数量)。状态群体与每个动作群体相连，计算Q值的是这些连接的突触权重。假设已经学习了正确的权重，状态神经元的输出将使每个动作群体表示在该状态下进行相关动作的价值(即Q(s, an))。
为了采取动作，模型需要根据这些Q值做出决策；这就是选择组件的目的。在我们的模型中，智能体遵循一个简单的贪婪策略，总是选择最高价值的动作。我们使用Stewart et al. (2010)描述的基底神经节模型计算最大操作量。该输出用于激活选择组件的网络内的抑制门，使对应于非选择动作的神经元群体不会被激活。选择组件的输出既是发送到误差计算网络(稍后讨论)的所选动作的价值，也是智能体的实际输出(即发送到环境的动作)。
智能体的操作与环境的细节无关；此模型被设计为在任何可以在SMDP框架中描述的任务中运行。所需的是，环境以某种方式获取智能体的输出(例如，"向左移动"之类的动作)，计算更新后的状态(例如，智能体的新位置)，并将新状态和收到的任何奖励发送回智能体。根据SMDP框架，状态转换可以随时发生，奖励可以随时发放。当新状态被发送到智能体时，它将修改状态群体中的活动，如等式4所示执行学习更新，智能体将决定新动作。
3.2 Representing and computing with neural activities
该模型完全在神经活动中运行，但它需要与环境交互并执行根据抽象数学变量定义的计算。为了在这两个域之间来回转换，我们使用神经工程框架(NEF; Eliasmith & Anderson, 2003)。
转化的第一部分是编码。例如，环境输出的抽象状态需要被编码到状态群体的活动中。假设状态由向量x表示(可能描述智能体的位置)。模型在连续时间内运行，因此随时间变化的状态可以用x(t)表示。输入信号被编码到状态群体的活动中，具体如下式：
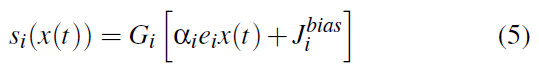
si(x(t))表示状态群体中神经元 i 的活动。Gi是神经元模型；在我们的例子中，我们使用LIF神经元。括号中的成分表示输入到神经元模型中的电流。α和
是神经元的参数，从生物学合理的范围内随机选择，分别代表增益和背景活动。向量ei识别神经元的首选刺激，即该神经元最敏感的输入空间的区域(这些也是随机选择的)。因此，每个神经元都会根据其内部参数和输入与神经元首选刺激的接近程度对输入做出响应。然后，整个群体的组合活动包括当前输入在输入空间中位置的分布式表示。注意，为了演示的目的，我们在这里描述了状态编码，这是一个通用机制，用于将任何输入编码到神经元群体的活动中。
转换的第二个方面是解码，将神经元群体的活动转换回一个抽象价值。例如，这允许将选择网络中的神经元活动解释为对环境的动作，或将动作群体的活动解释为Q值。这是通过对神经活动加权求和来实现的，具体如下式：
权重或解码器di可以通过下式计算：
f(x)给出解码编码值的(可能是非线性)函数的选项。然而，在大多数情况下，所需要的只是表示价值的恒等式，在这种情况下f(x)=x。通过这两个工具，编码和解码，我们可以在模型的神经活动与RL框架的变量和计算之间来回转换。
3.3 Learning
TD强化学习的基本过程是更新智能体对每个动作的值(Q值)的估计。在模型的架构中，这意味着修改状态和动作群体之间连接的突触权重。为了执行这些更新，我们使用了MacNeil & Eliasmith (2011)开发的误差调节神经学习规则，具体如下式：
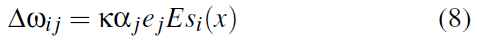
Δwij是神经元 i (在状态群体中)和神经元 j (在动作群体中)之间连接权重的变化。Κ是学习率，αj和ej是神经元 j 的性质(如等式5所示)，si(x)是神经元 i 的活动，E是误差。对于该模型，误差是Q值的期望变化，即等式4中的ΔQ(s, a)。这是一个神经学合理的权重更新，因为它只利用神经元 j 上可用的局部信息(假设所有神经元也接收到误差信号E)。MacNeil & Eliasmith (2011)表明，这种学习规则将导致权重被调整以最小化E，这意味着随着时间的推移，权重将计算出所需的Q值。
3.4 Error calculation
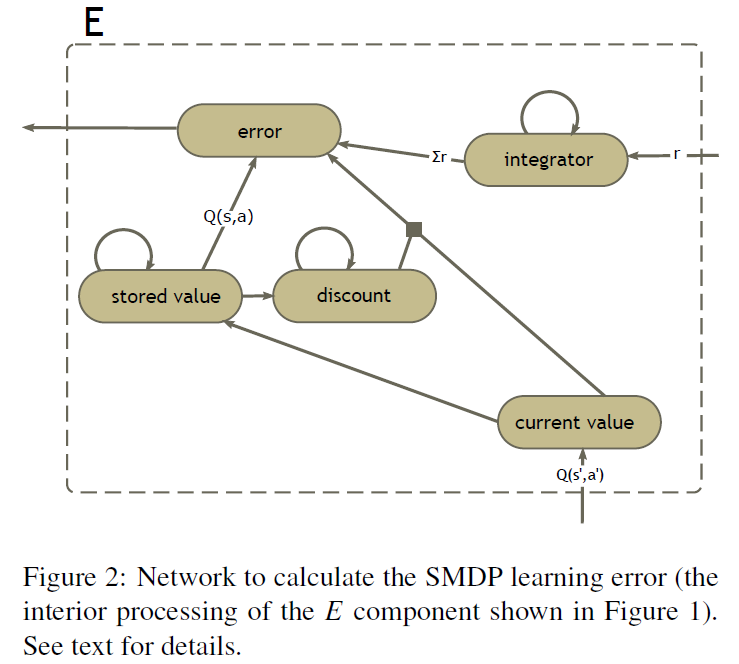
前一节提出了误差E来自何处的问题。也就是说，等式4是如何计算的？执行此计算的网络如图2所示。注意，这是图1中所示的E组件，它接收图1中所示的输入(所选动作的Q值和来自环境的奖励)。
一个挑战是将获得的奖励累加(等式4中的总和)。这是由网络的右上角组件完成的。累加群体的中心特征是循环联系，这使得它能够在缺乏输入的情况下保持其活动。这意味着，当新的奖励进入群体时，它们将被添加到已经被代表的先前奖励中，因此，群体表示给定奖励的总和。Eliasmith (2005)描述了如何建立循环网络来执行这些计算的细节。
"当前价值"群体表示当前选定动作的价值。第一次选择动作时，此值将转移到左下角的"存储价值"群体中。同样，这是一个群体，它将通过其循环连接保持其表示价值。当状态转换发生时，底部群体将表示新状态Q(s', a')中所选动作的价值，而"存储价值"群体将保持Q(s, a)。
折扣是通过对"存储价值"群体中表示的价值进行累加来计算的，使用与对传入奖励进行累加时相同的循环设置。然后从当前的Q输入中减去该价值，以计算折扣的动作价值。这与等式4中所表示的折扣不同，但它具有类似的计算效果：它减少了未来状态的价值，这与经过的时间和状态价值成比例。
因此，最终的"误差"群体拥有计算SMDP学习更新所需的所有部分。它将累积的奖励和折扣后的Q(s', a')值相加，然后减去存储的Q(s, a)值，从而得到神经学习规则所需的误差信号(等式8)。
4. Results
我们在一个空间导航任务(与Potjans et al. (2009)使用的任务相同)上测试了该模型。该智能体被随机放置在一个5 x 5的网格中，其四周是墙。智能体的状态是它在网格中的x，y位置，可用的动作是在四个主要方向上的移动。选择其中任何一个动作都将导致智能体朝该方向移动一格，除非它试图移动到墙中，在这种情况下，它保持在相同的位置。智能体在每个状态下的时间是随机确定的，范围在600到900毫秒之间。任务是移动到某个固定的目标位置。这相当于一个水迷宫类型的任务，其中的智能体不知道目标可能在哪里，必须通过探索环境来找到它。当智能体发现目标状态时，只要它保持在该状态，它就会获得固定奖励1。经过一段时间后，智能体被移动到一个随机位置，并且必须再次找到目标。
图3显示了模型在任务中花费大约2小时仿真时间后学习到的策略的示例。箭头显示四个运动方向的加权和，其中权重是与每个动作相关联的学到的Q值。由于智能体选择价值最高的动作，它将在最接近箭头方向的任何一个主方向上移动。轮廓表示最高价值动作的价值(即状态价值函数)。可以看出，尽管存在随机的时间延迟，但是智能体已经成功地学习了一个策略，该策略将从任何位置将其带到目标状态。
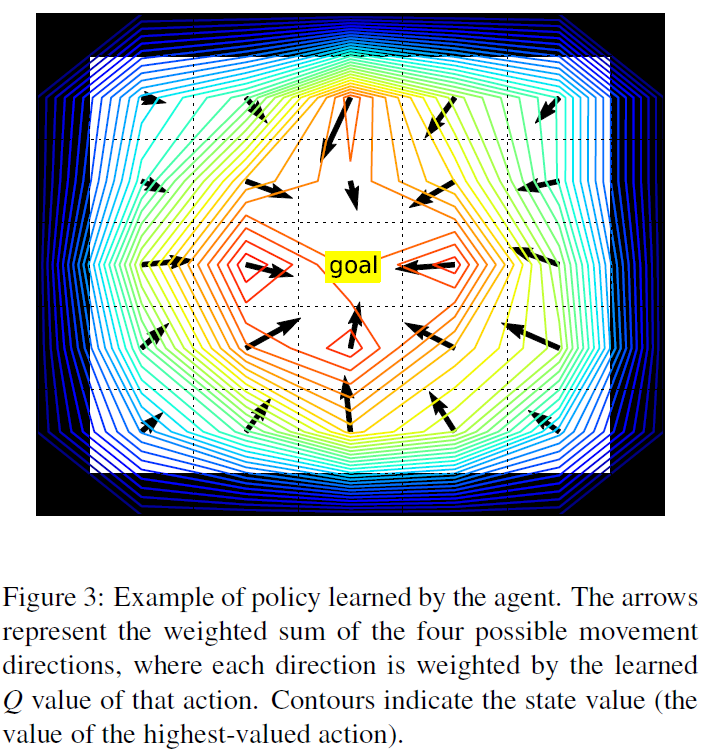
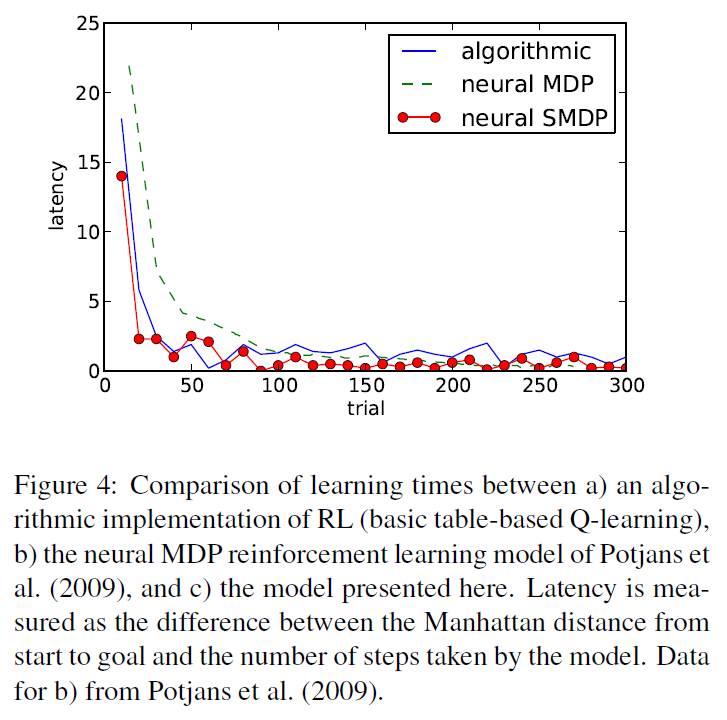
图4显示了我们模型的学习次数与Potjans et al. (2009)的学习次数之间的比较，以纯计算的RL实现为基准线。当智能体被放置在网格中的一个随机位置时，试验开始，当它到达目标时结束(此时它被放置在下一个试验的新位置)。我们效仿Potjans et al.，使用延迟来衡量智能体对任务的学习程度。延迟定义为起始点和目标之间的曼哈顿距离(startx - goalx + starty - goaly)与模型所采取的步数之间的差异，其中曼哈顿距离是可能的最短路径长度。可以看出，我们的模型比Potjans et al.的模型表现得更好，与纯计算解大致相当。值得注意的是，我们的模型在更具挑战性的SMDP框架中运行，具有随机的时间延迟；Potjans et al.的模型不可能完成此任务。
SMDP还提供了一种更强大的语言来描述问题域，它允许将时间直接并入任务描述中。例如，图5显示了一个类似于图3的任务，但是某些状态(以灰色显示)需要较长的时间才能让智能体通过(通过在通常随机确定的状态转换时间上添加3秒来仿真)。这意味着，通往目标的最有效的途径不再是直接的途径；智能体已经学会了权衡绕行的成本和通过缓慢区域的成本。时间通常是现实任务的重要组成部分，因此，将时间直接纳入智能体学习的能力是SMDP框架的另一个优势。
5. Discussion
我们提出了一种新颖的自主RL神经模型。该模型能够解决复杂的任务，这些任务需要一个扩展的动作序列来实现奖励，这在基于生物学的神经模型中是很少见的。此外，它还能够在现实的SMDP环境中解决这些任务，其中在动作选择、状态转换和奖励之间存在潜在的随机且未知的延迟。我们相信这是目前唯一一个能够实现这种性能的神经模型。
该模型在拓展神经RL模型功能能力的道路上还只是一个早期的步骤，有很多方法可以改进。首先，可以在模型中加入更多的神经细节。例如，结合更真实的脉冲神经元，可以与神经记录进行更详细的比较。对该模式的另一个改进将是对探索采取更原则的做法。目前，通过在动作价值进入选择成分时向其注入随机噪声(标准ε-贪婪方法的神经近似)来完成探索。然而，在未来，最好对探索过程有更多的控制权，这样，例如，智能体可以根据其目前的知识，决定进行多少探索。
未来工作的另一个途径是将该系统的学习组件集成到一个更完整的智能体模型中。该模型的输入和输出是抽象的，忽略了感觉加工和运动输出的复杂性。然而，我们实验室最近的工作已经开发出一种集成的大脑模型，能够感知视觉输入，对其进行内部处理，并控制运动输出(Eliasmith et al., 2012)。该模型能够进行联想RL，但不能进行更复杂的学习。将此模型的能力加入到详细的神经智能体中，可以研究从输入到输出的整个RL过程。
该模型所揭示的最有趣的可能性之一是构建一个能够分层RL (Barto & Mahadevan, 2003)的神经模型。在分层RL中，智能体选择的"动作"可以通过定义整个新行为的子程序来扩充。例如，智能体不只是在"向左"、"向右"等选项之间进行选择，其选项之一可以是"走到门口"，这将导致一系列旨在将智能体带到该位置的决策。所有层次化方法的共同点是，它们使用SMDP框架作为底层结构。动作和状态转换之间的未知时间延迟可用于封装高级动作执行的时间。SMDP框架允许智能体合并这些时间延迟和奖励，并学习如何在其复杂的操作集之间正确选择。我们在这里提出的这种模型是朝着能够进行分层学习和决策的功能性神经模型迈出的一步。