python打印杨辉三角

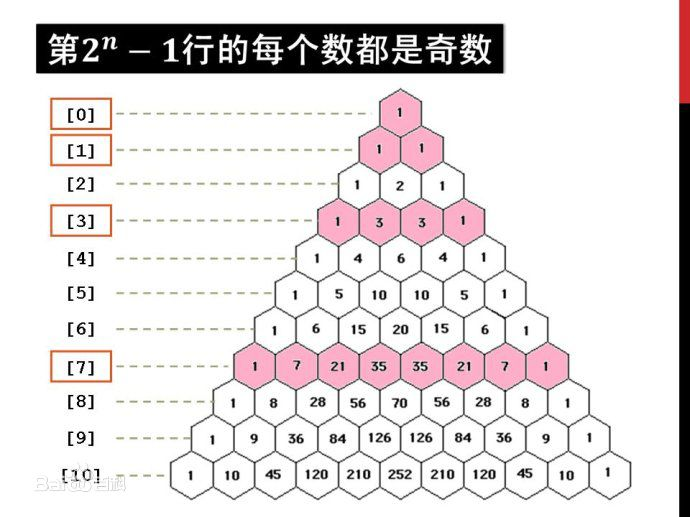
杨辉三角，是二项式系数在三角形中的一种几何排列

1. 每个数等于它上方两数之和。
2. 每行数字左右对称，由1开始逐渐变大。
3. 第n行的数字有n项。
4. 第n行数字和为2n-1。
5. 第n行的m个数可表示为 C(n-1，m-1)，即为从n-1个不同元素中取m-1个元素的组合数。
6. 第n行的第m个数和第n-m+1个数相等 ，为组合数性质之一。
7. 每个数字等于上一行的左右两个数字之和。可用此性质写出整个杨辉三角。即第n+1行的第i个数等于第n行的第i-1个数和第i个数之和，这也是组合数的性质之一。即 C(n+1,i)=C(n,i)+C(n,i-1)。
8. (a+b)n的展开式中的各项系数依次对应杨辉三角的第(n+1)行中的每一项。

性质5和性质7是杨辉三角的基本性质，是研究杨辉三角其他规律的基础。

num=input('请输入行数：')
num =int(num)

list1 =[] #list 用来保存杨辉三角
for n in range(num):
    row =[1]  #保存行
    list1.append(row)

    if n ==0:
        print(row)
        continue
    for m in range(1,n):
        row.append(list1[n - 1][m - 1] + list1[n - 1][m])
    row.append(1)

    print(row)