洛谷P2158 [SDOI2008]仪仗队

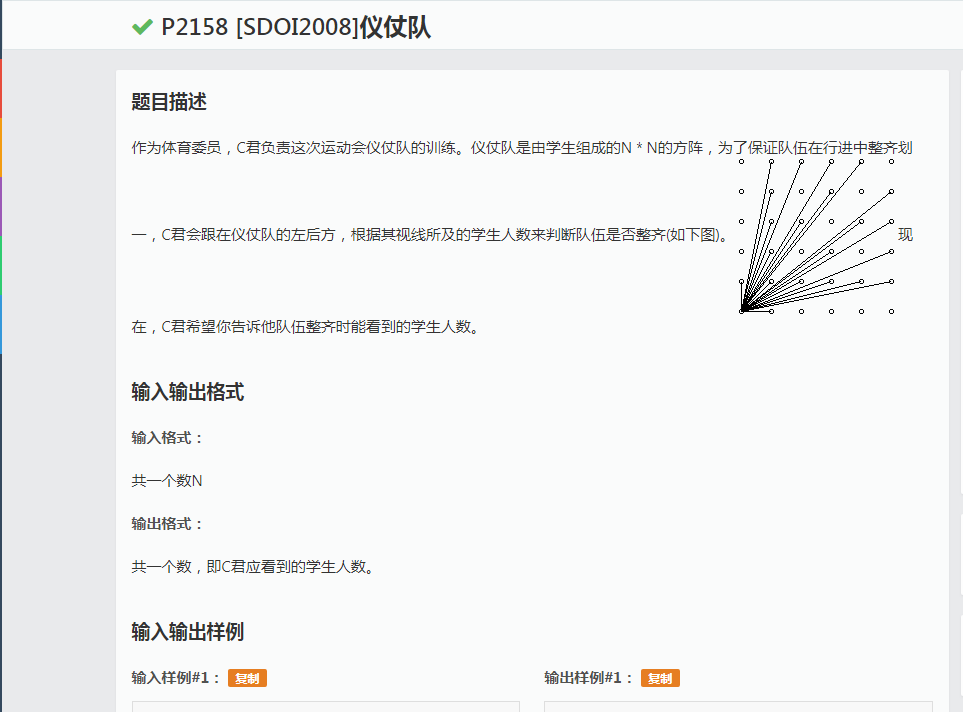
这道题仔细观察就会发现规律，设点的坐标为（X,Y）那么y=kx；

求不同的k值；k=y/x要k值不同x，y肯定要互质；可以随便观察一个点比如（1,4）

或者（3,2）这些可以看见的点都是x,y互质；

那么转化问题；

怎么才能求到这些点呢；

因为x<=n;y<=n;

那么就问题就变成了在小于n里面可以找到互质多少个的数；

设2<i<=n,引入欧拉函数，欧拉函数可以求小于等于i,有多少个与i互质的数;

为什么大于2？

因为横竖行都只能看1个，不然1于任何数都互质；

给出离线欧拉筛模板代码（大概是吧hhhh）

LL ans=2,a[maxn];
void init()
{
    for(int i=1;i<=maxn;i++)
        a[i]=i;
        a[1]=0;
        for(int i=1;i<=maxn;i++)
        {
            if(a[i]==i)
            {
             for(int j=i;j<=maxn;j+=i)
             a[j]=a[j]/i*(i-1);    
            }
        }
}

我们求的答案记为ans，ans=2(初值为2是因为加上横竖两行的）

求答案：ans+=a[i]*2(2<i<=n);(为什么乘以2?)

                                                                                （比如i=3，那么Φ(3)中2只算一种互质的可能性;但是坐标(x,y)就有两种可能性如(3,2),(2,3)

                                                                                  所以小于i的互质个数要乘以2才是要求答案)

                                                                                 %%%%陈玖言julao