给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
示例 1:
输入:s = "aa" p = "a"
输出:false
解释:"a" 无法匹配 "aa" 整个字符串。
示例 2:
输入:s = "aa" p = "a*"
输出:true
解释:因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此,字符串 "aa" 可被视为 'a' 重复了一次。
示例 3:
输入:s = "ab" p = ".*"
输出:true
解释:".*" 表示可匹配零个或多个('*')任意字符('.')。
示例 4:
输入:s = "aab" p = "c*a*b"
输出:true
解释:因为 '*' 表示零个或多个,这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。
示例 5:
输入:s = "mississippi" p = "mis*is*p*."
输出:false
提示:
0 <= s.length <= 20
0 <= p.length <= 30
s 可能为空,且只包含从 a-z 的小写字母。
p 可能为空,且只包含从 a-z 的小写字母,以及字符 . 和 *。
保证每次出现字符 * 时,前面都匹配到有效的字符
解题思路:简单来讲就是用一个字符规律串p去匹配我们的字符串s那么字符规律串中可能会有'.' 和 '*'用于不同的用途。'.' 是匹配任意单个字符,而'*'匹配零个或多个前面那一个元素。大家一定要看一下题目的事例去帮助自己理解这个题目。
解题思路:
S:abbba
P:ab*a
这里我们用s是abbba然后p是ab*a来作为我们的示例讲解,这是一道典型的动态规划题目,那么如图我们在初始化阶段需要初始化一个二维数组去存储每一个阶段的状态那么每一个方块中的元素代表什么呢?
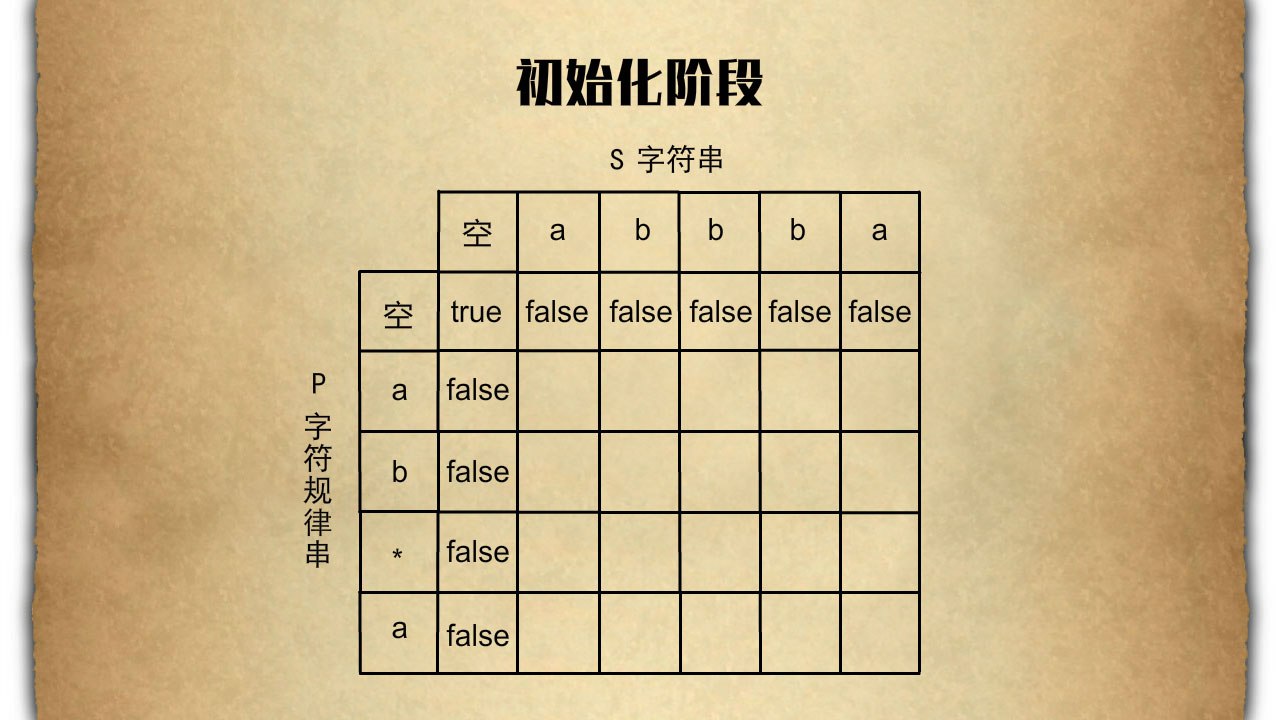
举例说明,图中的红色栗子对应着p是绿色区域a b *,红色栗子对应着s是黄色区域a b b那么他的意思就是我们用a b *去匹配字符串a b b。可以匹配的话就记录为true,不能匹配的就记录为false。特别的我们需要在p 和 s 前分别加一个空字符在初始化阶段时第一行除了空的第一个元素之外其他都是false只是因为p为空时我们并不能匹配s中任意有字母的字符串。而在第一列的初始化中我们需要比较小心因为如果说第二个元素是'*'那么a * 我们是可以匹配空字符串的所以我们在更新的时候需要做特别的处理,初始化阶段过后我们需要从左到右从上到下的更新一个二维数组。
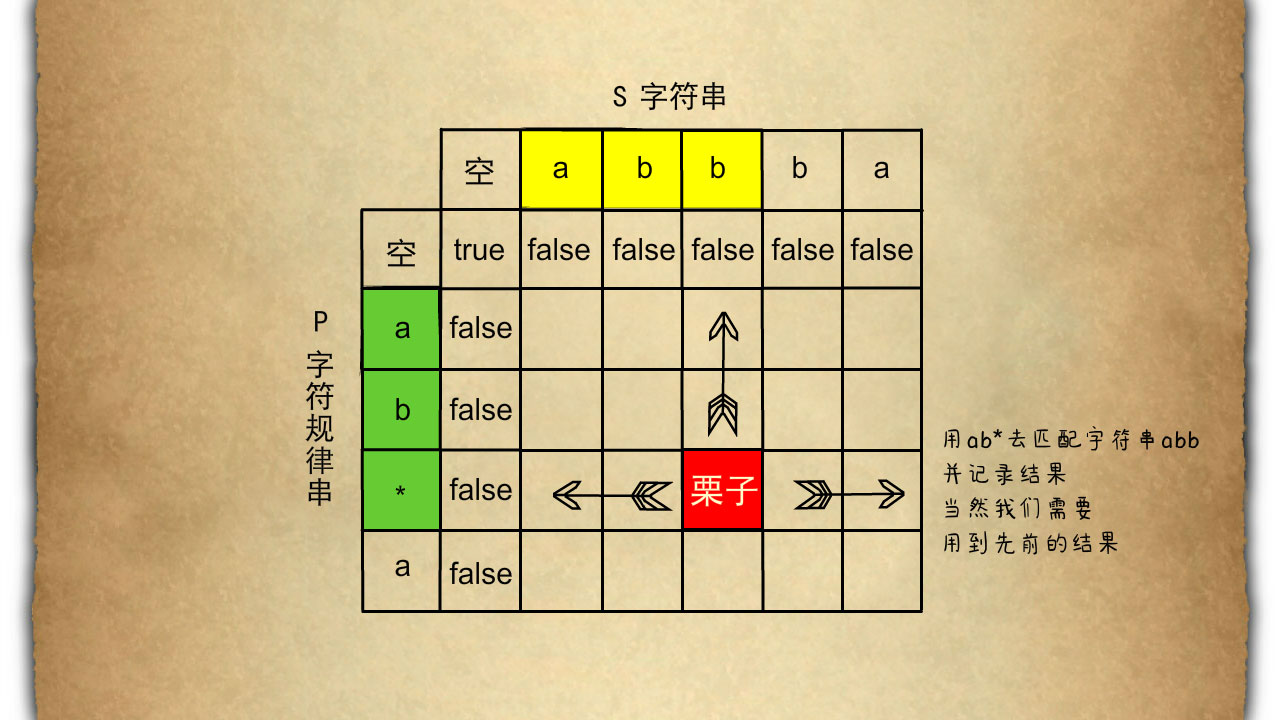
当P中元素不为'*'时,如图中蓝色格子所示我们只需要简单的匹配。s与p的当前字母是否相同而且左上角的元素是否为true如果是true的话我们更新当前方格为true依据这个法则我们可以将前面两行的元素更新。
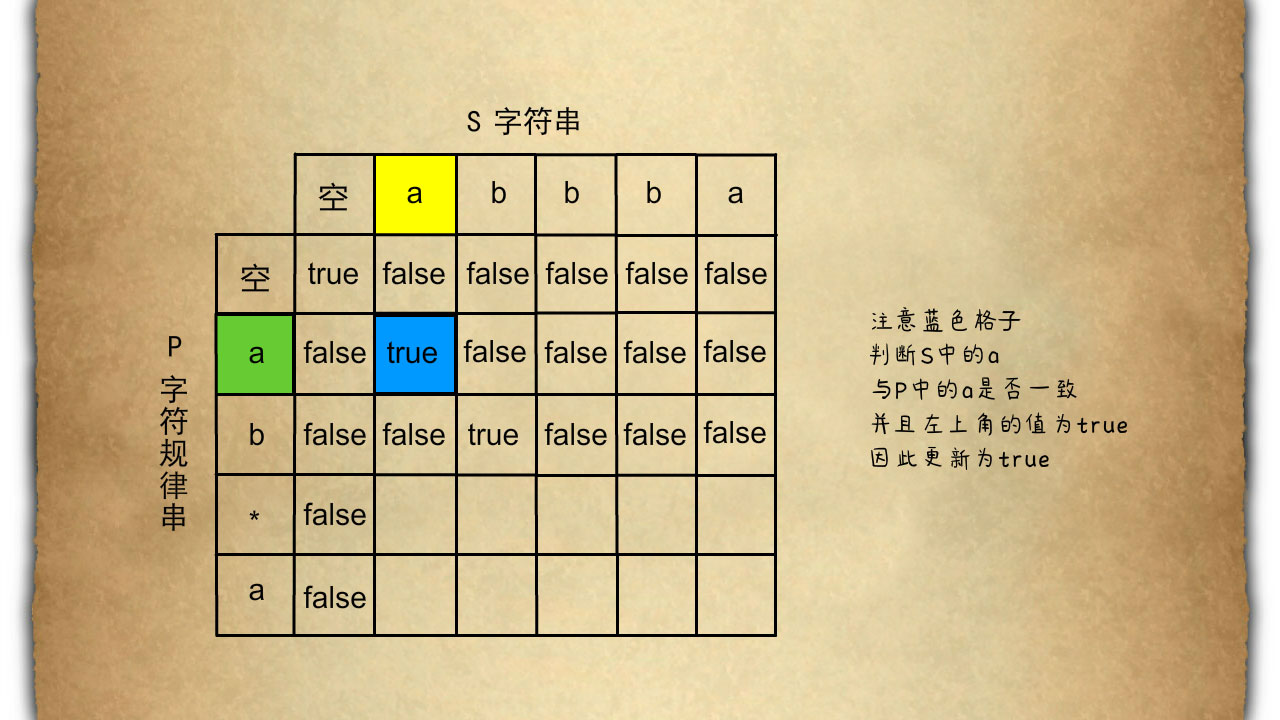
当我们更新到P的元素为'*'星号使我们有更多的情况需要考虑如图所示
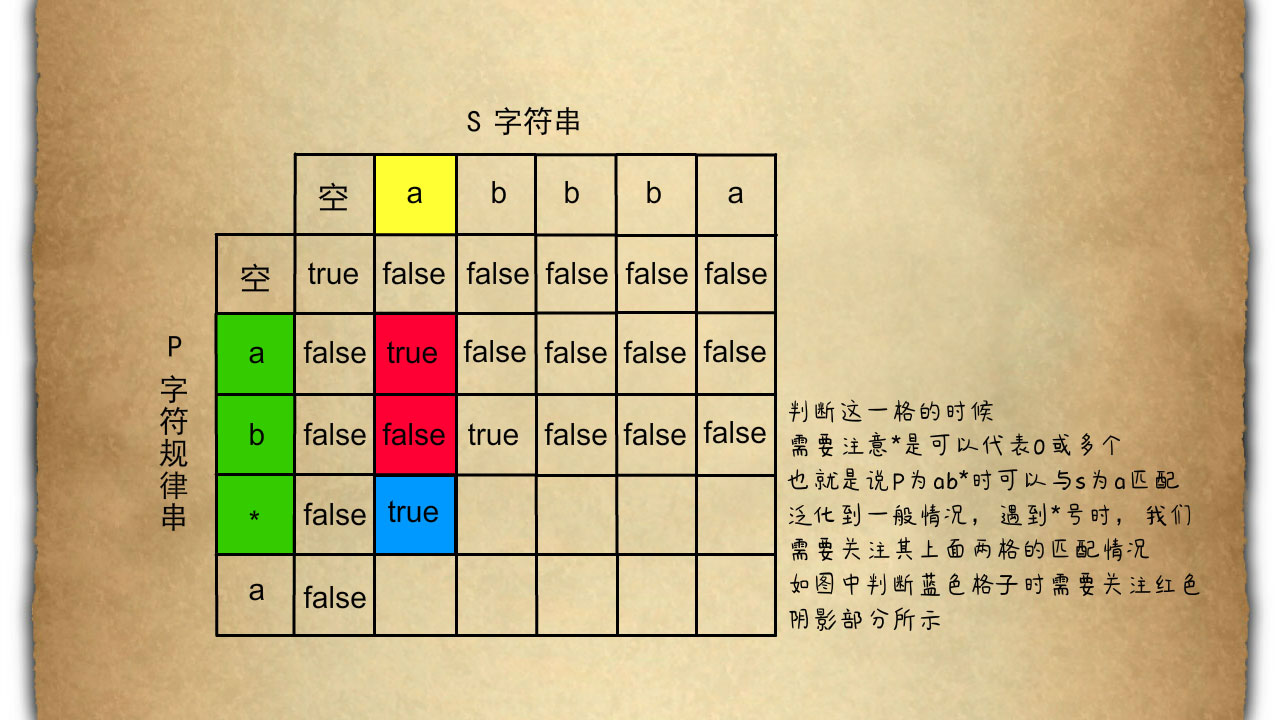
当我们在判断蓝色阴影合中的情况时我们需要小心 '*' 它是可以代表零个或多个,所以目前来说,ab*与s 为a时是可以匹配的因为我们可以把b当作零个处理。所以当我们在更新有'*'时我们需要关注,它的上面一格的情况以及上上一格的true或者false的情况去更新本格的信息。
还有另外一个情况需要考虑如图所示:
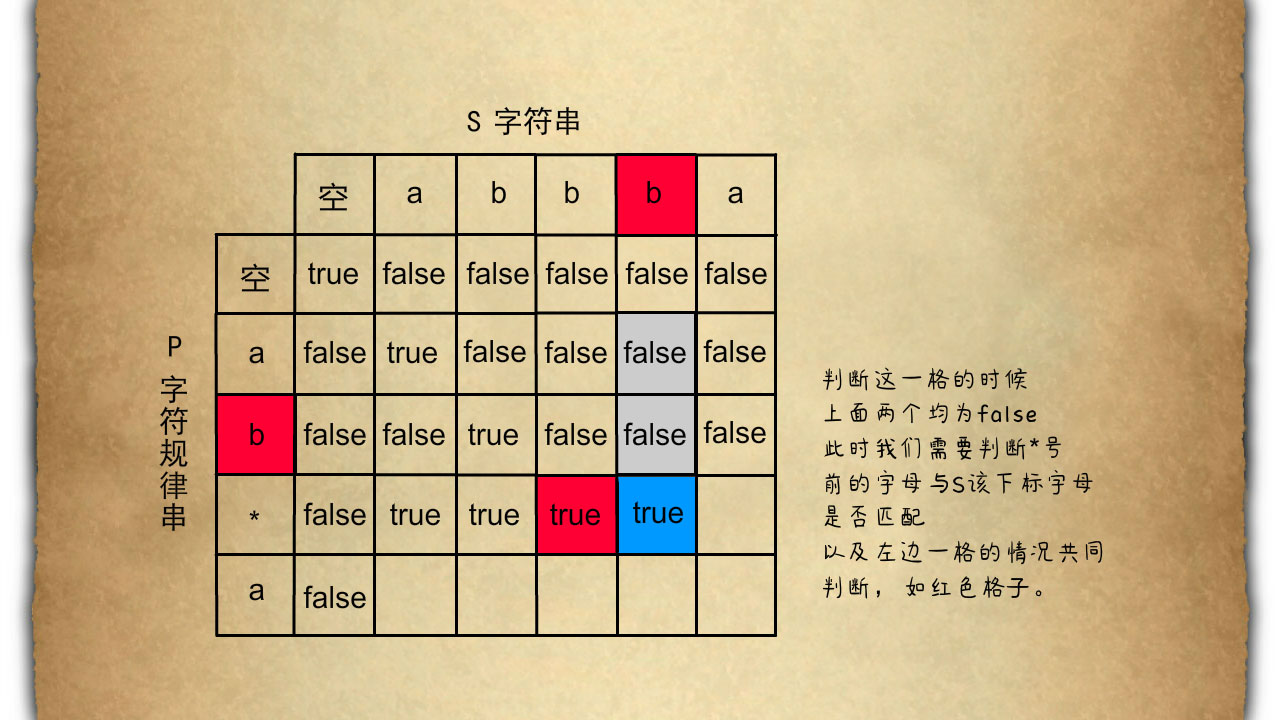
当我们在判断蓝色格子时,它的上面两个灰色格子。因为p为a或者p为ab时均不能与s 为abbb去相匹配,所以均为false。在这种情况下我们需要把s的当前字母b以及p的上一个字母在'*'前的字母b以及在前面一格的匹配状态也就是红色格子所示纳入考虑范围之内并综合判断。当s和p的两个当前字母是相同的而且前面的匹配状态也是true的时候,我们判断本格为true其余情况下都为false。
按照这一个统一的思路我们可以更新,二维数组中所有元素的信息在最后返回结果时我们只需要返回最后一个元素即可。
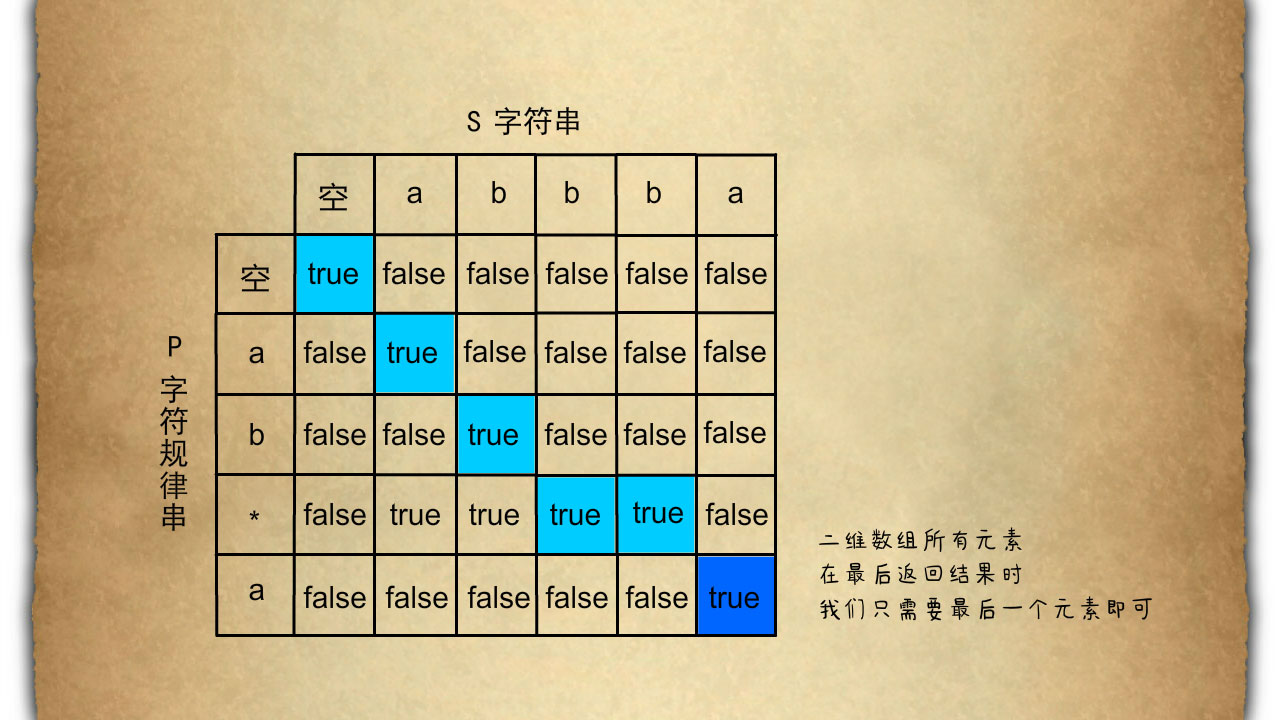
什么叫匹配,能连接成一条蓝色大龙这就叫匹配。
那么我们来看一下代码应该怎么写。首先开始就是我们的二维数组,那么我们需要对第一列进行比较特殊的初始化,然后根据思路中对P为星号以及不为信号时进行的区别对待我们可以将代码写出来因为题目中'.'点时可以作为任意字符所以我们还需要做一点特别的操作到这里我们的代码就全部写完了
class Solution: def isMatch(self,s:str,p:str) -> bool: dp = [[False]*(len(s)+1) for _ in range(len(p)+1)] #数组初始化 dp[0][0] = True for i in range(1, len(p)): dp[i + 1][0] = dp[i - 1][0] and p[i] == '*' for i in range(len(p)): for j in range(len(s)): if p[i] == "*": dp[i+1][j+1] = dp[i][j+1] or dp[i-1][j+1] if p[i-1] == s[j] or p[i-1] == '.': dp[i+1][j+1] |= dp[i+1][j] else:dp[i+1][j+1] = dp[i][j] and (p[i] == s[j] or p[i] == '.') return dp[-1][-1] so = Solution() print(so.isMatch('abbba','ab*a'))