vjudge地址 2019 ICPC Asia Yinchuan Regional
题意:给一个 n*n的矩阵,初始为0,进行若干次操作,每次操作可以使得矩阵的一行或一列的每一个元素加上一个正整数。现在给出操作后得到的矩阵,但是其中有一个元素未知(以-1标记),求出这个元素的值。
思路:先对与-1元素无关的行与列做处理,即将这些行或列的所有元素减去他们的最小值。
检查-1所在行与列除-1外的其他值,分别取除-1的最小值,再将两者加起来即可。
题意:
题意:定义![]()
给出n,求 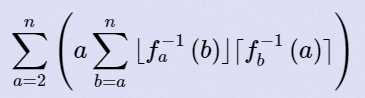 ,答案对998244353取模。
,答案对998244353取模。
思路:可知fa-1(x)=loga(x),因为b>=a>=2,所以fb-1(a)的上取整必为1。
考虑前一项loga(b)下取整,对于a2>b,该项为1;对于a3>b,该项为2......
然后枚举a,就可以根据ai>b(i>2),得到对答案的贡献(min(n+1,ai)-ai-1)*i
对于a2>b的情况,对答案贡献为∑i(n+1-i) - (n+∑(ai>b部分的i(n+1-i)) ),
前一项∑i(n+1-i)拆解得(n+1)∑i-∑i2,即(n+1)2n/2-n(n+1)(2n+1)/6
求就完事了。(取模会有点麻烦)具体见代码。

#include<cstdio> #include<cstring> #include<algorithm> using namespace std; typedef long long ll; ll now,ans,res; const int mod=998244353; ll pow(ll x,ll k) { ll re=1; while (k) { if (k&1) re=re*x%mod; x=x*x%mod; k>>=1; } return re; } int main() { ll i,j,n,x; ll res,re,ans; scanf("%lld",&n); ans=0; for (i=2;i<=n;i++) { now=0; for (j=0,x=i;x<=n;j++,x=x*i) now=(now+(min(n+1,x*i)-x)*j%mod)%mod; if (j==1) break; else ans=(ans+now*i%mod)%mod; } n=n%mod; res=(n+1)*n/2%mod*(n+1)%mod; re=n*(n+1)/2%mod*(2*n%mod+1)%mod*pow(3,mod-2)%mod; res=(res-re+mod)%mod; res=(res-n+mod)%mod; ans=(ans+res)%mod; printf("%lld ",ans); return 0; }
I
进制转换,x进制转为y进制(2<=x,y<=62)。
可以用Java做,先将x进制转为10进制再转为y进制。
N
