ARC106 游记
完了,这波要没脸见人了。 /dk

掉了 16 分。/dk
A 106
题意简述
给定整数 (n) ,询问是否存在正整数 (a,b) ,满足 (3^a+5^b=n) 。
(1le nle 10^{18}) 。
题目分析
直接无脑枚举 (a) 就行了,我一开始没有看清楚正整数,结果就错了两次。
参考代码
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define ch() getchar()
#define pc(x) putchar(x)
template<typename T>inline void read(T&x){
int f;char c;
for(f=1,c=ch();c<'0'||c>'9';c=ch())if(c=='-')f=-f;
for(x=0;c<='9'&&c>='0';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>inline void write(T x){
static char q[64];int cnt=0;
if(!x)pc('0');if(x<0)pc('-'),x=-x;
while(x)q[cnt++]=x%10+'0',x/=10;
while(cnt--)pc(q[cnt]);
}
int main(){
long long n,sm=5;read(n);
for(int b=1;sm<=n;++b,sm*=5){
long long tn=n-sm;int a=0;
while(tn>1&&tn%3==0)tn/=3,++a;
if(tn==1&&a>0){
return write(a),pc(' '),write(b),pc('
'),0;
}
}
puts("-1");
return 0;
}
B Values
题意简述
给定一个 (n) 个点 (m) 条边的无向图,第 (i) 个点一开始有一个点权 (a_i) ,每次可以让一条边连接的两个点 (u,v) 中的某一个的点权减一,另一个加一,询问能否使得所有第 (i) 个点的点权最终变成 (b_i) 。
(1le nle 2 imes 10^5,0le mle 2 imes 10^5,-10^9le a_i,b_ile 10^9) 。
题目分析
对于在一个连通块里面的点,它们两两之间的点权都是可以传递的,所以可以满足题目要求的充分必要条件就是每个连通块里面的 (a_i) 之和和 (b_i) 之和相等,直接并查集维护即可。
参考代码
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define ch() getchar()
#define pc(x) putchar(x)
template<typename T>inline void read(T&x){
int f;char c;
for(f=1,c=ch();c<'0'||c>'9';c=ch())if(c=='-')f=-f;
for(x=0;c<='9'&&c>='0';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>inline void write(T x){
static char q[64];int cnt=0;
if(!x)pc('0');if(x<0)pc('-'),x=-x;
while(x)q[cnt++]=x%10+'0',x/=10;
while(cnt--)pc(q[cnt]);
}
const int maxn=200005;
int a[maxn],b[maxn],pa[maxn];
int ac(int x){
return pa[x]==x?x:pa[x]=ac(pa[x]);
}
long long sz[maxn];
int main(){
int n,m;read(n),read(m);
for(int i=1;i<=n;++i)read(a[i]),sz[i]=a[i],pa[i]=i;
for(int i=1;i<=n;++i)read(b[i]);
while(m--){
int u,v;read(u),read(v);u=ac(u);v=ac(v);
if(u!=v)pa[u]=v,sz[v]+=sz[u];
}
for(int i=1;i<=n;++i)sz[ac(i)]-=b[i];int ok=true;
for(int i=1;i<=n;++i)if(ac(i)==i)ok&=(sz[i]==0);
puts(ok?"Yes":"No");
return 0;
}
C Solutions
题意简述
有一个这样的问题:给定 (n) 个闭区间 ([l_i,r_i]) ,请选出尽可能多的区间使得这些区间两两不相交。
有两个算法:第一个算法是将所有区间按 (r_i) 升序排序,然后从左往右能选就选;第二个算法是将所有区间按 (l_i) 升序排序,然后从左往右能选就选。
给定 (n,m) ,你需要构造这样 (n) 个闭区间,满足第一个算法选出来的区间数量减去第二个算法选出来的区间数量恰好为 (m) ,如果无解,输出 -1 。
(1le nle 2 imes 10^5,-nle mle n) ,你需要保证你输出的数字两两不同,并且都是整数,取值范围为 ([1,10^9]) 。
题目分析
首先要知道按第一个算法的方法去贪心就是正确的,这个很显然,所以当 (m) 为负数时无解;两种算法至少都会选出一个区间,并且当第一个算法可以选出 (n) 个区间的时候第二个算法一定也可以选出 (n) 个区间,所以第一个算法选出来的区间数量不可能比第二个算法大 (n-1) 个,所以当 (m) 大于等于 (n-1) 时也无解,这里需要额外注意的就是当 (n=1,m=0) 时是有解的。
当 (0le m<n-1) 时,必然是存在一种构造方案,这里介绍一下我的构造方案:
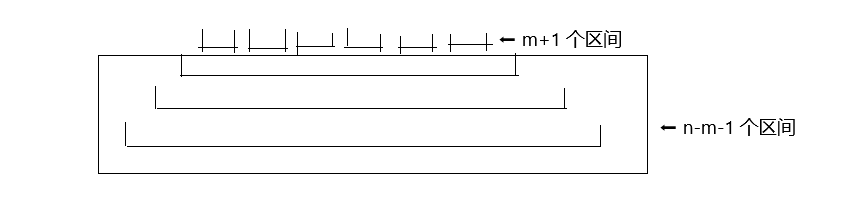
比赛的时候 WA 了两发,因为一开始没有注意到取值范围,没有特判 (n=1,m=0) 的情况。
参考代码
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define ch() getchar()
#define pc(x) putchar(x)
template<typename T>inline void read(T&x){
int f;char c;
for(f=1,c=ch();c<'0'||c>'9';c=ch())if(c=='-')f=-f;
for(x=0;c<='9'&&c>='0';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>inline void write(T x){
static char q[64];int cnt=0;
if(!x)pc('0');if(x<0)pc('-'),x=-x;
while(x)q[cnt++]=x%10+'0',x/=10;
while(cnt--)pc(q[cnt]);
}
int main(){
int n,m;read(n),read(m);
if(n==1&&m==0)puts("1 2");
else if(m>n-2||m<0)puts("-1");
else if(m==0){
for(int i=1;i<=n;++i)
write(i),pc(' '),write(i+n),pc('
');
}
else{
const int Base=300000;
for(int i=1;i<=m+1;++i)
write(i*2-1+Base),pc(' '),write(i*2+Base),pc('
');
int l=0,r=(m+1)*2+1;
for(int i=m+2;i<=n;++i)
write((l--)+Base),pc(' '),write((r++)+Base),pc('
');
}
return 0;
}
D Powers
题意简述
给定 (n) 个整数 (a_1,a_2,dots,a_n) 和整数 (k) ,对于任意的 (1le xle k) 求:
(2le nle 2 imes 10^5,1le kle 300,1le a_ile 10^8) 。
题目分析
这波是噩梦的开始,想看题解的直接跳到下面分割线处。
先讲一下我比赛时的情况,当时我看到 (x) 次方,心中大喜,打算直接拆斯特林数,于是。。。
令 (f(i,j)=sum_{t=i}^{n}{a_tchoose j}) ,那么:
令 (g(l,t)=sum_{s=0}^t{a_lchoose s}f(l+1,t-s)) ,那么:
后面的显然可以前缀和,如果不考虑求 (g(l,t)) ,那么时间复杂度就是 (mathcal O(nk+k^2)) 的,问题就是如何快速求出 (g(l,t)) ,发现 (g(l,t)) 是一个标准的卷积形式,所以可以用 NTT 在 (mathcal O(nklog_2k)) 的时间内解决,仔细想想,感觉挺悬,不过时限貌似是 3s ,而且模数强烈暗示 NTT ,于是赌一把,直接开始码。
然后就是这样。
没关系,看看排行榜冷静一下,然后就看到有人已经 AK 了。。。
这波是直接自闭好吧,也没有优化,也没有想到其他思路,时间也只有 30 分钟不到了,然后开始考虑放弃。
结果在比赛还剩 5 分钟的时候,临机一动,然后想到了下面的解题思路,然后疯狂码,最后总算是码完了,排名也从 600 多变成了 300 多,才没有掉得很惨。。。
事实上,这道题目只考了二项式定理。。。果然自己还是太先入为主了一点。。。
令 (h(t)=sum_{i=1}^na_i^t) ,那么
时间复杂度 (mathcal O(nk+k^2)) 。
参考代码
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define ch() getchar()
#define pc(x) putchar(x)
template<typename T>inline void read(T&x){
int f;char c;
for(f=1,c=ch();c<'0'||c>'9';c=ch())if(c=='-')f=-f;
for(x=0;c<='9'&&c>='0';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>inline void write(T x){
static char q[64];int cnt=0;
if(!x)pc('0');if(x<0)pc('-'),x=-x;
while(x)q[cnt++]=x%10+'0',x/=10;
while(cnt--)pc(q[cnt]);
}
const int maxn=200005,maxk=305,mod=998244353,inv2=(mod+1)/2;
int mo(const int x){
return x>=mod?x-mod:x;
}
int h[maxk],C[maxk][maxk];
int main(){
int n,k;read(n),read(k);
for(int i=1;i<=n;++i){
int a;read(a);
for(int j=0,sm=1;j<=k;++j,sm=1ll*sm*a%mod)
h[j]=mo(h[j]+sm);
}
C[0][0]=1;
for(int x=1;x<=k;++x){
C[x][0]=1;
for(int y=1;y<=k;++y){
C[x][y]=mo(C[x-1][y]+C[x-1][y-1]);
}
}
for(int x=1;x<=k;++x){
int ans=0;
for(int y=0;y<=x;++y){
ans=mo(ans+1ll*C[x][y]*inv2%mod*mo(mod-h[x]+1ll*h[y]*h[x-y]%mod)%mod);
}
write(ans),pc('
');
}
return 0;
}
E Medals
这道题目考场上没有写出来,不过觉得不应该,可能是一些特殊的图在应用方面还是没有很熟悉吧。
题意简述
有 (n) 个工人,第 (i) 个工人会先工作 (a_i) 天,然后休息 (a_i) 天,然后再工作 (a_i) 天……
每一天你只可以给当天来工作的工人中的一个颁发奖章,询问要让每一个工人获得至少 (k) 个奖章,至少需要多少天。
(1le nle 18,1le k,a_ile 10^5) 。
题目分析
考虑使用二分图来建模,假设过了 (x) 天,那么这个二分图左边有 (n imes k) 个点,分别表示每个工人的每一个奖章,右边有 (x) 个点,分别表示每一天,如果第 (i) 天工人 (j) 来了,那么右边的第 (i) 个点就向左边表示第 (j) 个工人的所有奖章连边,这样的话如果 (x) 天所有工人是可以获得 (k) 个奖章的,这张二分图的最大匹配就是 (n imes k) 。
根据 Hall 定理我们可以得出,这张二分图的最大匹配就是 (n imes k) 的充分必要条件就是对于左边任意的 (i) 个点,和这 (i) 个点中的任意一个有连边的右边的点的数量要大于等于 (i) 。左边的两个点如果代表的是同一个工人的两个奖章,那么它们连着的右边的点集是相同的,贪心地想,我们只需要考虑任意 (i) 个工人即可,相当于要求就是任意 (i) 个工人中至少一个工人来工作的天数要大于等于 (i imes k) 。
考虑到如果天数大于等于 (3nk) ,那么任何一个工人来工作的天数都大于等于 (n imes k) ,此时必然满足条件。
考虑二分天数 (x) ,然后统计任意 (i) 个工人中至少一个工人来工作的天数,这个可以补集转化为其他 (n-i) 个工人中只有这些工人来工作的天数,先用 (mathcal O(nk)) 的复杂度求恰好任意 (i) 个工人来工作的天数,然后通过前缀和来求只有,前缀和的复杂度是 (mathcal O(n2^n)) 的,这样的话总的复杂度就是 (mathcal O((nk+n2^n)log_2(nk))) ,还需要加上预处理每天是哪些工人来工作的复杂度,即 (mathcal O(n^2k)) 或者更优。
参考代码
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define ch() getchar()
#define pc(x) putchar(x)
template<typename T>inline void read(T&x){
int f;char c;
for(f=1,c=ch();c<'0'||c>'9';c=ch())if(c=='-')f=-f;
for(x=0;c<='9'&&c>='0';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>inline void write(T x){
static char q[64];int cnt=0;
if(!x)pc('0');if(x<0)pc('-'),x=-x;
while(x)q[cnt++]=x%10+'0',x/=10;
while(cnt--)pc(q[cnt]);
}
const int maxnk=6000006,maxk=100005;
int cnt1[1<<18],pos[maxnk],cnt[maxk],num[1<<18];
int main(){
int n,k;read(n),read(k);
for(int i=0;i<n;++i){
int a;read(a);cnt[a]^=1<<i;
}
int nk=n*k,nk3=3*nk;
for(int i=1;i<=100000;++i){
if(!cnt[i])continue;
for(int j=1;j<=nk3;j+=i)
pos[j]^=cnt[i];
}
int U=1<<n,_U=1<<(n-1),l=n*k,r=3*n*k;
for(int s=1;s<U;++s)cnt1[s]=cnt1[s&(s-1)]+k;
while(l<r){
int mid=(l+r)>>1,sum=0;
memset(num,0,sizeof num);
for(int i=1;i<=mid;++i){
sum^=pos[i];++num[sum];
}
for(int i=0;i<n;++i){
int d=(1<<i)-1;
for(int s=0;s<_U;++s){
int rs=(s&d)|((s&(~d))<<1);
num[rs|(1<<i)]+=num[rs];
}
}
int ok=true;
for(int s=0;s<U&&ok;++s)
ok&=((mid-num[(U-1)^s])>=cnt1[s]);
if(ok)r=mid;else l=mid+1;
}
write(l),pc('
');
return 0;
}
F Figures
这道题目没有写出来也算是一个遗憾。
题意简述
有 (n) 个有标号的点,第 (i) 个点有 (d_i) 个有标号的插孔,你需要连接恰好 (n-1) 对插孔使得这些点连通,其中一个插孔只可以连一条边,问方案数对 (998244353) 取模的值。
(2le nle 2 imes 10^5,1le d_i<998244353) 。
题目分析
这道题目真是一道神仙题。
先讲生成函数的做法。
如果第 (i) 个点的最终度数为 (a_i+1) ,那么它给答案造成贡献的时候就需要额外乘以 ({d_ichoose a_i+1}(a_i+1)!) ,考虑 prufer 序列和树一一对应,所以我们可以枚举每个点的度数减一:
构建插孔数量为 (t) 的指数型生成函数 (F_t(x)) :
答案就是:
再讲一下官方给出来的神仙构造做法。
考虑依次选边,最后再除以 ((n-1)!) ,给每个点钦定一个特殊的插孔,那么一开始特殊的插孔就有 (n) 个,不特殊的插孔就有 (sum_{i=1}^n(d_i-1)) 个,执行以下操作 ((n-2)) 次,在执行以下操作中的每一步的时候每一个特殊的插孔都表示一个连通块:
- 在所有不特殊的插孔中选出一个插孔。
- 在所有特殊的插孔中选出一个和之前选出来的不特殊插孔不连通的一个特殊插孔。
- 连接这两个插孔,删除选出来的这两个特殊插孔和不特殊插孔。
最后还会剩下两个特殊的插孔,表示还有两个连通块,直接连接这两个特殊的插孔。
可以发现,每一个特殊的插孔都是我们给这个点选择的最后一次连边,所以每一种依次连边方式的特殊插孔都是确定的,可以发现,这种构造方式和每一种依次连边方式都是一一对应的,所以依次连边的方案数就是这样子构造的方案数。
考虑这样子构造的方案数,首先选出特殊插孔 (prod_{i=1}^nd_i) ,如果操作从 0 开始编号,那么在第 (k) 次的操作中,选择不特殊的插孔的方案数就是 ((sum_{i=1}^n(d_i-1)-k)) ,选出特殊插孔的方案数就是 ((n-k-1)) ,所以依次连边的方案数就是:
记得除以 ((n-1)!) ,所以答案就是:
参考代码
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define ch() getchar()
#define pc(x) putchar(x)
template<typename T>inline void read(T&x){
int f;char c;
for(f=1,c=ch();c<'0'||c>'9';c=ch())if(c=='-')f=-f;
for(x=0;c<='9'&&c>='0';c=ch())x=x*10+(c&15);x*=f;
}
template<typename T>inline void write(T x){
static char q[64];int cnt=0;
if(!x)pc('0');if(x<0)pc('-'),x=-x;
while(x)q[cnt++]=x%10+'0',x/=10;
while(cnt--)pc(q[cnt]);
}
const int mod=998244353;
int mo(const int x){
return x>=mod?x-mod:x;
}
int main(){
int n,S=0,T=1;read(n);
for(int i=1;i<=n;++i){
int d;read(d);
T=1ll*T*d%mod;
S=mo(S+d);
}
S-=n;
for(int i=0;i<n-2;++i,--S)
T=1ll*T*S%mod;
write(T),pc('
');
return 0;
}
总结
这次比赛还是暴露了很多的问题的,下一次争取不要再犯这种 nt 错误了。