容斥原理学习笔记
本文可能有的地方叙述不太严谨,还烦请大家指正。
简介
容斥原理,简单来说,就是计数时为了不重复计算,先忽略重复再排斥掉重复的一种计数方法或者思想。
容斥原理常用的两个公式如下:
其中,对于第二个公式,更加常用是以下这个式子:
设 \(U=\bigcap_{i=1}^nA_i\) ,那么我们认为 \(\left|\bigcap_{i\in\varnothing}\overline{A_i}\right|=|U|,\left|\bigcup_{i\in\varnothing}A_i\right|=0\) 。
\((2)\) 和 \((3)\) 本质上是一样的,证明如下:
这里给出一种证明容斥原理的方法(以 \((1)\) 为例):
对于任意一个集合 \(S\in[n]\) ,定义 \(S'=(\bigcap_{i\in S}A_i)\bigcap(\bigcap_{j\in\overline{S}}\overline{A_j})\) ,那么,对于任意两个不相同的集合 \(S_1,S_2\) ,都满足 \(S_1'\bigcap S_2'=\varnothing\) (即 \(S_1'\) 和 \(S_2'\) 互斥),并且 \(\bigcup_{S\in [n]}S'=U\) 。
不妨考虑 \(S'\) 中的元素被计算得到的系数和是多少,计算 \(S'\) 中的元素会在计算任意的 \(T\in S,T\ne\varnothing\) 时计算得到,设 \(\left|S\right|=m\) ,那么 \(S'\) 中的元素被计算得到的系数就是:
由此我们可以得出, \(U\) 中的每个元素被计算得到的系数都恰好为 \(1\) ,于是便证明了式子 \((1)\) 。
式子 \((2)\) 也是类似的,这里就不再做证明。
扩展
更一般的凑容斥系数的办法
从以上证明过程中得到启发,或许我们可以找到更一般的“凑”容斥系数的方法,不妨假设恰好被 \(x\) 个集合覆盖的元素,贡献为 \(f(x)\) ,大小为 \(x\) 的集合的容斥系数为 \(g(x)\) ,那么类似上述证明过程可以得到:
令 \(g(0)=0\) ,那么可以得到:
于是,我们便得到了更加一般的“凑”容斥系数的方法。
不妨举个例子吧,类似二进制运算一般的,我们定义集合间的运算 \(\operatorname{Xor}\) ,那么如何计算 \(\left|\operatorname{Xor}_{i=1}^nA_i\right|\) 呢?
在这个式子中,有 \(f(x)=[2 \not\mid x]\) ,于是我们可以得到( \(m\ne 0\) ):
于是我们便得到了容斥系数,便可以得到如下式子:
例题
洛谷P4515:[COCI2009-2010#6] XOR 。
这道题显然就可以直接用我们推出的式子:
问题转化为求若干三角形的交得到的面积,在这道题目中,三角形交三角形得到的也是三角形,于是就变成了求两个三角形相交得到的顶点坐标和腰长。
分类讨论,两个三角形的相对位置有如下几种情况(设两个三角形的参数分别为 \(x_1,y_1,r_1\) 和 \(x_2,y_2,r_2\) ,其中 \(x_1\le x_2\) ,交得的三角形参数为 \(x,y,r\) ):
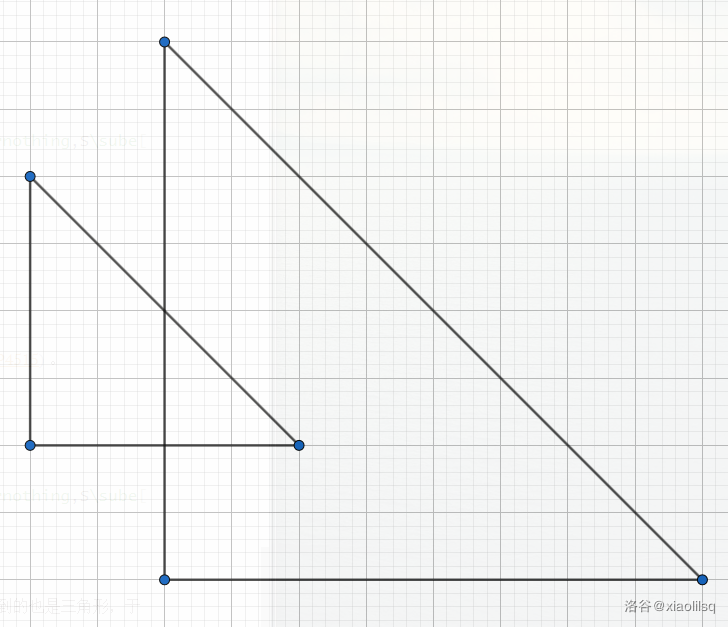
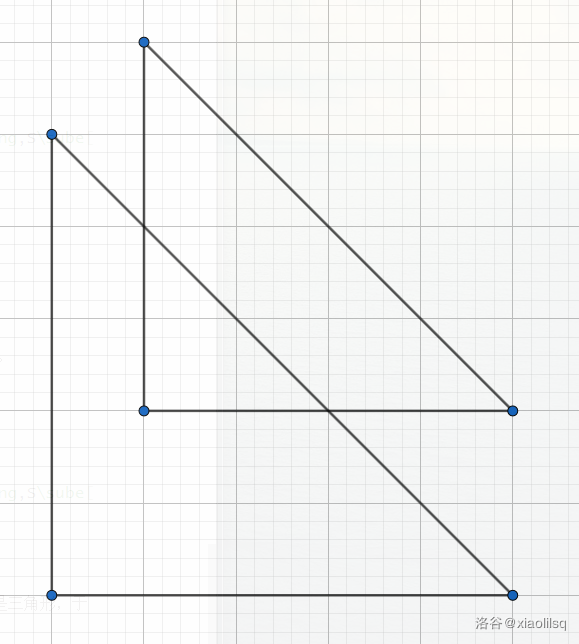
其实分类讨论完可以得到以下结论:
于是就不用分类讨论了。
前缀和与差分
很久以前我们就学过使用容斥原理来求前缀和。
给定一个 \(n\) 维数组 \(a\) ,求它的前缀和,我们有这个式子:
当维数较低的时候,这个式子很显然,随着维数的增加,使用容斥来求前缀和貌似越来越不那么直观了。
在继续往下讲之前,我们不妨利用一开始的式子来证明一下前缀和所用的容斥系数的正确性。
首先,我们不妨把数组上面每个值 \(x\) ,认为是 \(x\) 个互异的元素,不同的位置上面的值之间也没有相交的地方,于是前缀和就可以表示为若干个集合的并集的大小。
不妨假设我们当前求的前缀和是 \((c_1,c_2,c_3,\dots,c_n)\) ,设这个位置上的集合为 \(x\) , \(A_i=(c_1,c_2,c_3,\dots,c_i-1,\dots,c_n)\) ,那么我们相当于求的就是:
其实 \(\left|\bigcap_{i\in S}A_i\right|=(c_1-[1\in S],c_2-[2\in S],\dots,c_n-[n\in S])\) ,所以容斥的系数就是 \((-1)^{|S|+1}\) 。
类似的,我们也学过使用前缀和数组来求原数组,也就是差分。
给定一个 \(n\) 维数组 \(a\) ,求它的差分数组,我们有这个式子:
就是上面的式子移完项后的结果,就不再证明了。
莫比乌斯反演
莫比乌斯反演的本质就是容斥原理的应用,不妨使用容斥原理的思想来证明一下莫比乌斯反演。
先摆出莫比乌斯反演的式子:
不妨使用一种奇怪的方法来理解一个正整数 \(x\) ,先把所有的质数顺次排列成 \(p_1,p_2,\dots\) ,然后我们把 \(x\) 质因数分解变成 \(p_1^{k_{x,1}}p_2^{k_{x,2}}\dots p_n^{k_{x,n}}(k_{x,i}\ge 0)\) ,然后我们就认为 \(x\) 是一个 \(n\) 维点 \((k_{x,1},k_{x,2},\dots,k_{x,n})\) ,一个正整数 \(y\mid x\) ,当且仅当 \(\forall 1\le i\le n,k_{x,i}\ge k_{y,i}\) ,由此我们可以看出, \(F(x)\) 本质上就是在求 \(f(x)\) 的一个 \(n\) 维前缀和!
那么如何通过 \(F(x)\) 得到 \(f(x)\) 呢?使用差分!把之前的式子摆出来:
再把一个点理解回去变成一个整数,发现对于某个数 \(d\mid n\) , \(F(d)\) 给 \(f(n)\) 的贡献就是看 \(\frac{n}{d}\) 能否表示成若干个互异质数的乘积,如果不能这样表示系数就是 \(0\) ,否则就通过看质数的数量来决定容斥系数,而这,就是 \(\mu(\frac{n}{d})\) 的定义。
\(\rm Min-Max\) 容斥
给定集合 \(S\) ,那么有:
如何证明?不妨我们先假设 \(S\) 内的元素都是正整数,然后对于每一个正整数值 \(x\) ,定义一个集合 \(A_x=\{1,2,3,\dots,x\}\) ,那么 \(x=\left|A_x\right|\) , \(\min(x,y)=\left|A_x\cap A_y\right|\) , \(\max(x,y)=\left|A_x\cup A_y\right|\) ,然后根据一开始的容斥原理的式子就可以证明了。
如果 \(S\) 里面的元素并非都是正整数,类比一下就可以得到这个式子也是成立的。
扩展容斥原理
容斥原理只能求所有元素的并集和交集,那么可不可以求恰好 \(k\) 个集合的交集呢?
其实是可以的,参见“更一般的凑容斥系数的办法”,先写出这个式子:
其中 \(f(i)=[i=k]\) ,于是:
设我们要求的东西是 \(Q_k\) ,可以得到:
扩展 \(\rm Min-Max\) 容斥
设 \(\max(S,k)\) 表示集合 \(S\) 中第 \(k\) 大的值,扩展 \(\rm Min-Max\) 容斥给出了 \(\max(S,k)\) 和 \(\min(T)\) 的关系。
和 \(\rm Min-Max\) 容斥一样的分析方法,先假设所有元素都是正整数, 把每个元素看做是一个集合,不妨先给每个值从大到小排个序,那么第 \(k\) 大的值怎么求呢?
考虑恰好被 \(k\) 个集合覆盖的元素数量实质是什么,就是 \(S\) 中第 \(k\) 大的值减去第 \(k-1\) 值,所以 \(S\) 中第 \(k\) 大的值就是恰好被 \(i(i\ge k)\) 个集合覆盖的元素总和!于是我们得到:
模型
数数类问题
简介
其实我也不知道这类问题该如何称呼,暂且叫它“数数类问题”吧。
问题描述:给定 \(m\) 个正整数 \(a\) ,询问一段区间 \([l,r]\) 内有多少数能被这些数中至少一个整除。
首先差分,差分完之后就变成了询问 \(1\) 到 \(n\) 内有多少数能被 \(m\) 个数中至少一个整除,然后设 \(A_i=\{x\mid 1\le x\le n\&\&a_i\mid x\}\) ,根据容斥原理的公式:
问题变成求同时能被其中若干个数整除的数的个数,即被它们的 \(\operatorname{lcm}\) 整除的数的个数,这样问题就变得好求起来了。
当然有的时候我们要求的是不被任何一个数整除,那么此时用到的就是这个公式:
莫比乌斯函数容斥法
有时,我们并不直接使用莫比乌斯反演,而仅仅是使用莫比乌斯函数,这里通过一道例题来说明。
例题
洛谷P4318:完全平方数
注意一下,这里认为 \(1\) 不是完全平方数。
首先二分答案,问题变成求所有小于等于某个数并且不是某个完全平方数的正整数倍的数的个数。
不难发现,我们只要考虑所有质数的平方就行了,质数平方的 \(\operatorname{lcm}\) 等于质数 \(\operatorname{lcm}\) 的平方等于质数积的平方,这时有一种思路,就是直接枚举集合 \(S\) ,由于每个数都是被若干个质数乘积唯一表示,我们这样枚举构造出来的数两两之间是互异的,枚举得到的数的最大值也是小于等于 \(\sqrt{答案最大值}\) 的,所以时间复杂度应该是严格 \(\sqrt{\text{答案最大值}}\) 的,但是这种方法有一个地方需要注意,等一会再讲。
考虑另外一种方法,直接考虑每一个数被枚举到的时候的容斥系数,当这个数是 \(1\) 的时候,容斥系数是 \(1\) ,是一个质数的时候,容斥系数是 \(-1\) ,是 \(x\) 个互异质数的乘积的时候,容斥系数是 \((-1)^x\) ,如果这个数不能表示为若干个互异质数的乘积的话,它就不可能被枚举到,而这些恰好就是莫比乌斯函数的定义!
所以我们求小于等于某个数 \(x\) 并且不是某个完全平方数的正整数倍的数的个数,就相当于是求以下这个式子:
可以直接求,也可以用整除分块,但是优化效果不明显。
如何优雅地枚举集合
其实这个和容斥原理貌似没有任何关系,因为这里讲到的将会是有关代码实现的问题,由于我之前落入过这个坑中,所以还是讲一下吧。
考虑这样一个问题:给定 \(m\) 个互质的正整数 \(a\) ,询问 \(1\) 到 \(n\) 内有多少数能不被这些数中任何一个整除。
上面刚刚提到的例题可以用莫比乌斯函数较好的解决,但是这题就不太好用这种方法做了,不难发现一个数如果能被这 \(m\) 个整数表示,那么这个表示一定是唯一的,所以枚举集合的理论时间复杂度也是对的,我们不妨使用枚举集合的办法。
一种方法是使用 dfs ,枚举每一个整数的幂,如果大于 \(n\) 就直接返回,枚举到底的时候就计算贡献:
int a[maxm],m,n,ans;
void dfs(int no,int sm,int rv){
if(no==m+1)return ans+=n/sm*rv,void();
dfs(no+1,sm,rv);
if(1ll*sm*a[no]<=n)
dfs(no+1,sm*a[no],-rv);
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;++i)
scanf("%d",&a[i]);
dfs(1,1,1);
printf("%d\n",ans);
}
这样做的复杂度其实是错的,因为一个数字在 dfs 过程中出现次数不止一次,正确的写法应该是这样的:
int a[maxm],m,n,ans;
void dfs(int no,int sm,int rv){
ans+=n/sm*rv;
for(int i=no+1;i<=m&&1ll*sm*a[i]<=n;++i)
dfs(i,sm*a[i],-rv);
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;++i)
scanf("%d",&a[i]);
sort(a+1,a+m+1);
for(int i=1;i<=m;++i)
dfs(i,a[i],-1);
dfs(m+1,1,1);
printf("%d\n",ans);
}
当然, dfs 也可以用 bfs 代替。
其实如果使用错误写法往往也不会超时,因为在这道题中两种写法的差距可能体现得不够明显,可以尝试使用 dfs 或者 bfs 利用所有 \(n\) 以内的质数的幂遍历到 \(n\) 以内的所有数字。
这里给出使用 bfs 遍历所有数字的方法,大家可以试一下使用那种错误的写法可不可以跑过去:
const int n=10000000,maxn=n+5;
int tot,vis[maxn],pri[maxn],qn[maxn],qs[maxn];
int main(){
for(int i=2;i<=n;++i){
if(!vis[i])
pri[++tot]=i;
for(int j=1;j<=tot;++j){
int t=i*pri[j];if(t>n)break;
vis[t]=true;if(i%pri[j]==0)break;
}
}
memset(vis,0,sizeof vis);
vis[1]=true;
int fro=0,bac=0;
for(int i=1;i<=tot;++i)
qn[bac]=i,qs[bac]=pri[i],++bac;
while(fro<bac){
int no=qn[fro];long long sm=qs[fro];++fro;
for(int i=1;sm<=n;++i,sm*=pri[no]){
for(int j=no+1;j<=tot&&1ll*sm*pri[j]<=n;++j)
qn[bac]=j,qs[bac]=sm*pri[j],++bac;
vis[sm]=true;
}
}
int i,ok=true;
for(i=1;i<=n&&ok;++i)
ok&=vis[i];
write(i),pc('\n');
return 0;
}
一一对应问题
好吧,其实这个名字也是我随手起的。
简介
这类问题就是给出一个对应关系,要求的是恰好一一对应的方案数。
一般情况下,设一种方案为 \(T\) ,我们都是设集合 \(A_i=\{T|i\text{对应的数量}\ge 1\}\) ,然后要求的就是:
\(\overline{A_i}=\{T|i\text{对应的数量}=0\}\) ,而 \(\left|\bigcap_{i\in S}\overline{A_i}\right|\) 就相当于是不考虑集合 \(S\) 求出来的任意对应的方案数。
例一
洛谷P3349:[ZJOI2016]小星星
这里认为树上的点和图上面的点一一对应。
套用上面所讲的,枚举哪些小星星不需要考虑,于是问题就变成了求树和图之间任意对应的方案数,此时就可以很简单地 \(\rm dp\) 做了,设 \(dp(i,j)\) 表示树上点 \(i\) 及其整棵子树都已经对应完毕,并且点 \(i\) 和图上点 \(j\) 对应的方案数,然后枚举树上面的每个儿子及其对应图上面的点进行转移。
例二
洛谷P4336:[SHOI2016]黑暗前的幻想乡
这里认为树上的边和建筑公司编号一一对应。
一样地,套用上面所讲的,枚举哪些建筑公司不需要考虑,然后直接用 \(\rm Matrix-tree\) 定理就可以求任意对应的答案了。