适合不熟悉矩阵求导的人,我会尽量用数学公式和图解的方式来详细地推导BP算法。
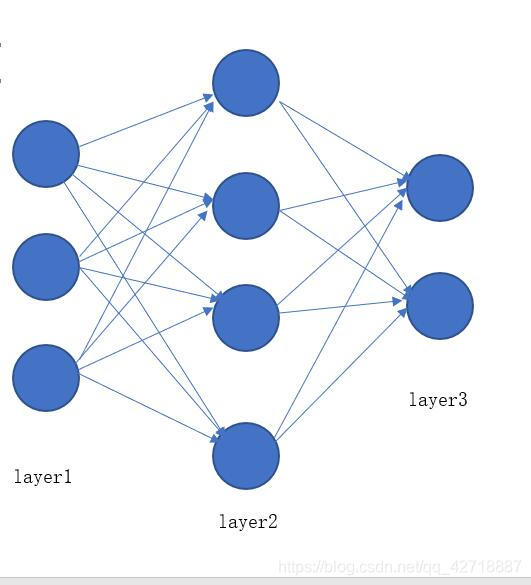
标记规定
θ
j
k
l
mathop heta
olimits_{jk}^l
θjkl:代表连接第l层第k个神经元和第l+1层第j个神经元的权重参数。
z
j
l
mathop z
olimits_j^l
zjl: 代表第l层第j个神经元的输入。
a
j
l
mathop a
olimits_j^l
ajl: 代表第l层第j个神经元的输出。
σ
sigma
σ :代表激活函数。
δ
j
l
mathop delta
olimits_j^l
δjl :代表第l层第j个神经元产生的错误。
L:代表神经网络的层数(这里可以理解为3)。
c :代表代价函数(不太明白的话可以就直接理解为关于输出层a的函数)。
这里的规定标记不熟悉的话可以看一下吴恩达大佬的机器学习课程。
公式一(反向传播最后一层的错误)
我们不采用向量的形式来推导,这里仅是涉及到标量的计算。
根据定义:
δ
j
l
mathop delta
olimits_j^l
δjl =
δ
C
δ
z
j
l
frac{{delta {
m{C}}}}{{delta mathop z
olimits_j^l }}
δzjlδC(学过微积分的同学肯定很好理解,这里的错误就是反应了这个神经元对代价函数的影响有多大)。
由链式法则可以得到:
δ
j
L
mathop delta
olimits_j^L
δjL =
δ
C
δ
a
j
L
frac{{delta {
m{C}}}}{{delta mathop a
olimits_j^L }}
δajLδC *
δ
a
j
L
δ
z
j
L
frac{{delta {
m{ mathop a
olimits_j^L}}}}{{delta mathop z
olimits_j^L }}
δzjLδajL。这两个式子就很容易算出来,第一个在已知C的时候很容易就求出来了,第二个的话因为
a
j
l
mathop a
olimits_j^l
ajl =
σ
sigma
σ(
z
j
L
mathop z
olimits_j^L
zjL),所以也很容易求出来(但是这里特别要注意的是因为我们反向传播的时候是只是知道
a
j
L
mathop a
olimits_j^L
ajL的值,所以需要用
a
j
L
mathop a
olimits_j^L
ajL来计算
σ
sigma
σ '(
z
j
L
mathop z
olimits_j^L
zjL)的值)。
然后,我们用向量的形式来计算:
δ
L
mathop delta
olimits^L
δL =
δ
C
δ
a
L
frac{{delta {
m{C}}}}{{delta mathop a
olimits^L}}
δaLδC .*
δ
a
L
δ
z
L
frac{{delta {
m{ mathop a
olimits^L}}}}{{delta mathop z
olimits^L }}
δzLδaL。(这个.*就是对应元素相乘)。就这里的网络结构来看
δ
L
mathop delta
olimits^L
δL算出来就是一个2×1的向量。
公式二(每一层的误差计算)
同样还是从标量的形式来看:
δ
j
l
mathop delta
olimits_j^l
δjl =
δ
C
δ
z
j
l
frac{{delta {
m{C}}}}{{delta mathop z
olimits_j^l }}
δzjlδC(这里可以把l看做2)。则由链式法则可得:
δ
j
l
mathop delta
olimits_j^l
δjl =
∑
k
δ
C
δ
z
k
l
+
1
×
δ
z
k
l
+
1
δ
a
j
l
×
δ
a
j
l
δ
z
j
l
sum
olimits_k {frac{{delta C}}{{delta mathop z
olimits_k^{l + 1} }}} {
m{ imes }}frac{{delta mathop z
olimits_k^{l + 1} }}{{delta mathop a
olimits_j^l }}{
m{ imes }}frac{{delta mathop a
olimits_j^l }}{{delta mathop z
olimits_j^l }}
∑kδzkl+1δC×δajlδzkl+1×δzjlδajl。我解释一下为什么要做这个k的累和,首先我们来看这样一张图(就是这里第一层映射到第二层的图):
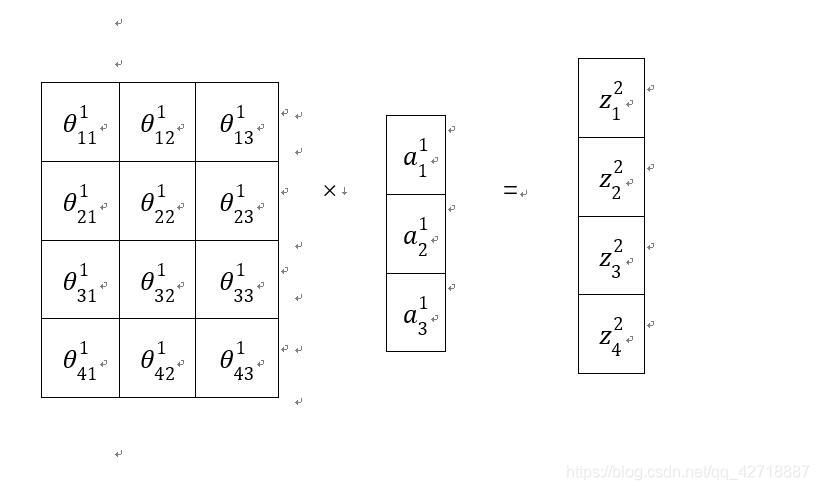
从这个矩阵乘法就可以看出来每一个
a
j
1
mathop a
olimits_j^1
aj1对
z
k
2
mathop z
olimits_k^2
zk2都有贡献,所以这里需要求和才能算出
δ
j
l
mathop delta
olimits_j^l
δjl。
所以:
δ
j
l
mathop delta
olimits_j^l
δjl =
∑
k
δ
j
l
+
1
×
θ
k
j
l
×
σ
′
(
z
j
l
)
sum
olimits_k{mathop delta
olimits_j^{l+1}×mathop heta
olimits_{kj}^l×sigma'(mathop z
olimits_j^l)}
∑kδjl+1×θkjl×σ′(zjl)。
然后我们再来看看矩阵形式的表示(如果熟悉矩阵求导的话就可以不用看了),同样还是先看一张图:
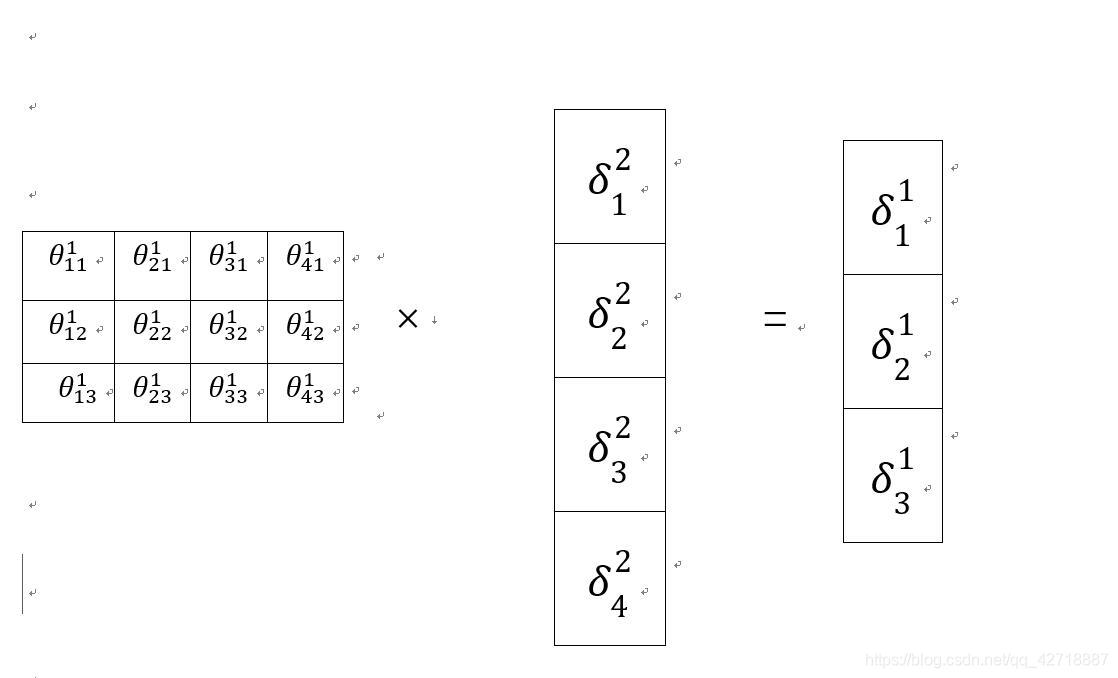
这个图就是刚刚向量方式计算出来的错误的矩阵计算形式,这里可以看出来θ是要转置的,于是我们便得出了
δ
l
mathop delta
olimits^l
δl 的矩阵表示形式。
δ
l
mathop delta
olimits^l
δl =
(
θ
l
.
T
∗
δ
l
+
1
)
.
∗
σ
′
(
z
j
l
)
(mathop heta
olimits^l.T * mathop delta
olimits^{l+1}) .* sigma'(mathop z
olimits_j^l)
(θl.T∗δl+1).∗σ′(zjl)。
公式三(权重θ的梯度)
BP算法的最终目的便是要求出来权重的梯度以便于更新权重,所以接下来我们看看权重的梯度是如何计算的。
同样先是看看在标量之下如何计算:
δ
C
δ
θ
j
k
l
=
δ
C
δ
z
j
l
+
1
×
δ
z
j
l
+
1
δ
θ
j
k
l
=
δ
j
l
+
1
×
a
k
l
frac{{delta C}}{{delta mathop heta
olimits_{jk}^l }}{
m{ = }}frac{{delta {
m{C}}}}{{delta mathop z
olimits_j^{l + 1} }}{
m{ imes }}frac{{delta mathop z
olimits_j^{l + 1} }}{{delta mathop heta
olimits_{jk}^l }} = mathop delta
olimits_j^{l + 1} {
m{ imes }}mathop a
olimits_k^l
δθjklδC=δzjl+1δC×δθjklδzjl+1=δjl+1×akl。
然后用矩阵进行表示,还是先看一张图,注意:这里右边那个是θ梯度矩阵,不是θ的矩阵(主要是博主比较懒,不想画了):
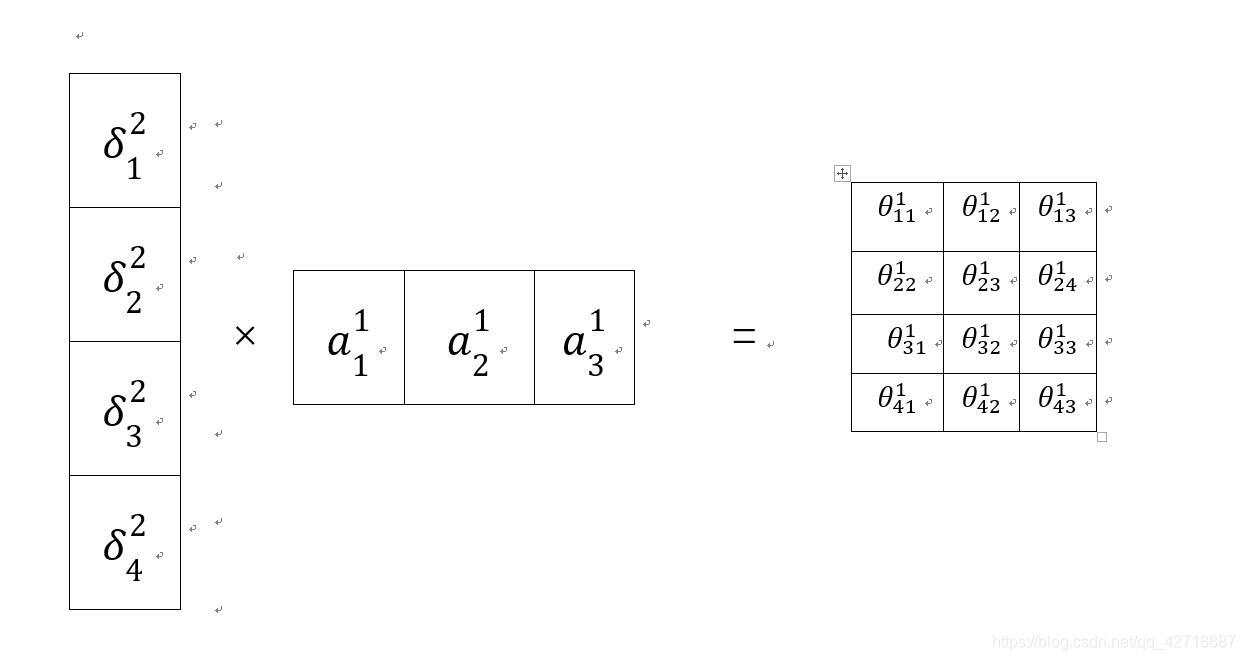
以上就是BP算法的推导,如果熟悉矩阵求导的话就可以跳过那些图片啦,博主主要是想用一种更直观的方式来介绍BP算法。当然还有偏置bias的求导,大家可以自己这样推一推。