首先说下母函数定义:
生成函数即母函数,是组合数学中尤其是计数方面的一个重要理论和工具。生成函数有普通型生成函数和指数型生成函数两种,其中普通型用的比较多。形式上说,普通型生成函数用于解决多重集的组合问题,而指数型母函数用于解决多重集的排列问题。母函数还可以解决递归数列的通项问题(例如使用母函数解决斐波那契数列的通项公式)。
母函数的精髓:
1.“把组合问题的加法法则和幂级数的乘幂对应起来”
2.“母函数的思想很简单 — 就是把离散数列和幂级数一 一对应起来,把离散数列间的相互结合关系对应成为幂级数间的运算关系,最后由幂级数形式来确定离散数列的构造."
关于母函数的定义及了解先看下百度百科,之后再看这篇文章

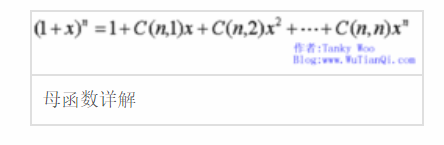
对于序列a0,a1,a2,…构造一函数:

有1克、2克、3克、4克的砝码各一枚,能称出哪几种重量?每种重量各有几种可能方案?
考虑用母函数来解决这个问题:
我们假设x表示砝码,x的指数表示砝码的重量,这样:
1个1克的砝码可以用函数1+1*x^1表示,
1个2克的砝码可以用函数1+1*x^2表示,
1个3克的砝码可以用函数1+1*x^3表示,
1个4克的砝码可以用函数1+1*x^4表示,
上面这四个式子懂了吗
我们拿1+x^2来说,前面已经说过,x表示砝码,x的指数表示砝码的重量!初始状态时,这里就是一个质量为2的砝码。
那么前面的1表示什么?按照上面的理解,1其实应该写为:1*x^0,即1代表重量为2的砝码数量为0个。
所以这里1+1*x^2 = 1*x^0 + 1*x^2,即表示2克的砝码有两种状态,不取或取,不取则为1*x^0,取则为1*x^2
我们这里结合前面那句话:
“把组合问题的加法法则和幂级数的乘幂对应起来“
这里的系数砝码个数,这里的指数是砝码的重量。
1+x^2,也就是1*x^0 + 1*x^2,也就是上面说的不取2克砝码,此时有1种状态;或者取2克砝码,此时也有1种状态。
几种砝码的组合可以称重的情况,可以用以上几个函数的乘积表示:
(1+x)(1+x^2)(1+x^3)(1+x^4)
=(1+x+x^2+x^4)(1+x^3+^4+x^7)
=1 + x + x^2 + 2*x^3 + 2*x^4 + 2*x^5 + 2*x^6 + 2*x^7 + x^8 + x^9 + x^10
从上面的函数知道:可称出从1克到10克,系数便是方案数。(!!!经典!!!)
例如右端有2^x^5 项,即称出5克的方案有2种:5=3+2=4+1;同样,6=1+2+3=4+2;10=1+2+3+4。
故称出6克的方案数有2种,称出10克的方案数有1种 。
下边就是第二个例子:
求用1分、2分、3分的邮票贴出不同数值的方案数:
大家把这种情况和第一种比较有何区别?第一种每种是一个,而这里每种是无限的。
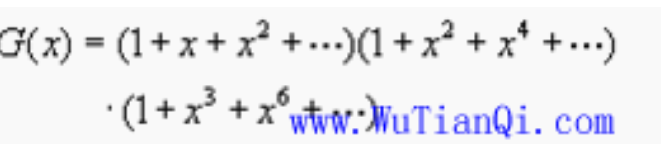
以展开后的x^4为例,其系数为4,即4拆分成1、2、3之和的拆分方案数为4;
即 :4=1+1+1+1=1+1+2=1+3=2+2
这里再引出两个概念"整数拆分"和"拆分数":
所谓整数拆分即把整数分解成若干整数的和(相当于把n个无区别的球放到n个无标志的盒子,盒子允许空,也允许放多于一个球)。
整数拆分成若干整数的和,办法不一,不同拆分法的总数叫做拆分数。、
#include<iostream> using namespace std; const int _max=10001; int c1[_max], c2[_max]; int main(){ int num; int i,j,k; while(cin>>num){ for(i=0;i<=num;i++) //这里是对c1的初始化,由于刚开始是一个表达式(1+x+x^2+..x^n) 。 { //即把质量从0到n的所有砝码的都初始化为1. c1[i]=1; //c1是保存各项质量砝码可以组合的数目 ,c2是一个中间量 c2[i]=0; } for(i=2;i<=num;i++){ // i从2到n遍历,这里i就是指第i个表达式, //上面给出的第二种母函数关系式里,每一个括号括起来的就是一个表达式。 for(j=0;j<=num;j++) // j 从0到n遍历,这里j就是(前面i個表达式累乘的表达式)里第j个变量,。如(1+x)(1+x^2)(1+x^3),j先指示的是1和x的系数,i=2执行完之后变为 //(1+x+x^2+x^3)(1+x^3),这时候j应该指示的是合并后的第一个括号的四个变量的系数。 for(k=0;k+j<=num;k+=i){ //k表示的是第j个指数,所以k每次增i(因为第i个表达式的增量是i),也就是说第一个表达式如果和下一个表达式结合的话增量是i. c2[j+k]+=c1[j]; //这里是把 当指数是j+k时,等于加上指数为j的组合数。 } for(j=0;j<=num;j++){ c1[j]=c2[j]; //把c2的值赋给c1,而把c2初始化为0,因为c2每次是从一个表达式中开始的。 c2[j]=0; } } cout<<c1[num]<<endl; } return 0; }
这是一个万能模板,基本上大多数组合类题都可以用这个方法,有的可以直接用,不过大多都需要修改部分
直接用的例题:http://acm.hdu.edu.cn/showproblem.php?pid=1028
需修改下的:http://acm.hdu.edu.cn/showproblem.php?pid=1398
这里我想说一下这个题:http://acm.hdu.edu.cn/showproblem.php?pid=1171
要想做出这题,需要理解这个模板
利用母函数法来解决,因为分成两堆,而两堆中较小的一堆最大为所有物品总价值量的一半,所以母函数的组合数上下就可以设置成总价值量的一半。求出所有的组合后,可以利用贪心的思想来得到答案,因为要求两堆之差尽可能小,所以就可以从总价值量的一半开始向小的方向找,找到最大的价值量,则另一堆的价值量就是总价值量-此堆的价值量。因为组合数可能较大,这里不记录组合种数,而是用一个标记来表示该数能否组合出即可。
#include <iostream>
using namespace std;
int c1[250010], c2[250010];
int value[55];
int amount[55];
int main()
{
int nNum;
while(scanf("%d", &nNum) && nNum>0)
{
memset(value, 0, sizeof(value));
memset(amount, 0, sizeof(amount));
int sum = 0;
for(int i=1; i<=nNum; ++i)
{
scanf("%d %d", &value[i], &amount[i]);
sum += value[i]*amount[i]; //这些物品的总价值量
}
memset(c1, 0, sum*sizeof(c1[0]));
memset(c2, 0, sum*sizeof(c2[0]));
for(int i=0; i<=value[1]*amount[1]; i+=value[1]) //初始化第一个表达式
c1[i] = 1;
int len = value[1]*amount[1]; //第一个表达式的长度
for(int i=2; i<=nNum; ++i)
{
for(int j=0; j<=len; ++j) //表达式长度是不断变化的
for(int k=0; k<=value[i]*amount[i]; k+=value[i]) //记住这里变的是value[i],因为增量是value[i];
{
c2[k+j] += c1[j];
}
len += value[i]*amount[i];
for(int j=0; j<=len; ++j)
{
c1[j] = c2[j];
c2[j] = 0;
}
}
for(int i= sum/2; i>=0; --i)
if(c1[i] != 0)
{
printf("%d %d
", sum-i, i);
break;
}
}
return 0;
}
推荐:HDOJ:1709,1028、1709、1085、1171、1398、2069、2152
参考博客:http://www.wutianqi.com