NCD 2019 C. Hasan and his lazy students

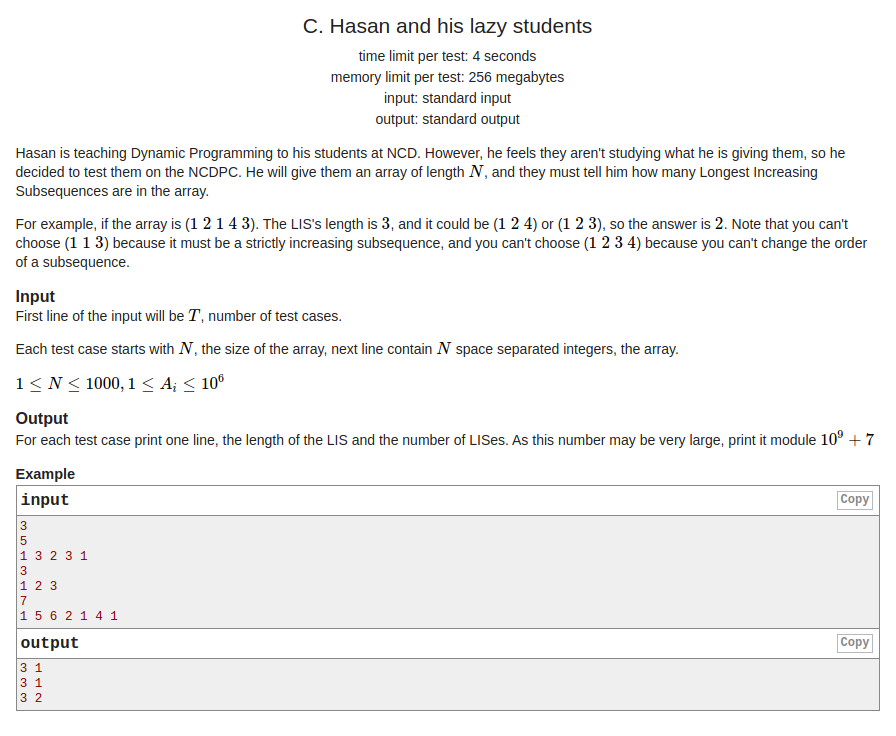
• 题意:给你一组数,求最长的严格上升子序列及个数(mod 1e9+7)

• 题解:用动态规划来求LIS,记\(dp[i]\)是数组中第i个位置上的数的LIS最优解,我们遍历一遍原数组,然后找i位置前的LIS,如果\(a[j]<a[i]\)并且\(dp[j]+1>dp[i]\)那么当前i位置的最优解就应该更新成\(dp[j]+1\).然后我们再记一个\(res[i][length]\),表示i位置上长度为length的LIS的个数.最后统计一下长度最长的子序列有多少个就行了.

• 代码:

  #include <iostream>
  #include <cstdio>
  #include <cstring>
  #include <cmath>
  #include <algorithm>
  #include <stack>
  #include <queue>
  #include <vector>
  #include <map>
  #include <set>
  #include <unordered_set>
  #include <unordered_map>
  #define ll long long
  #define fi first
  #define se second
  #define pb push_back
  #define me memset
  const int N = 1e6 + 10;
  const int mod = 1e9 + 7;
  using namespace std;
  typedef pair<int,int> PII;
  typedef pair<long,long> PLL;
   
  int t;
  int n,a[N];
  ll res[2000][2000];
  int dp[N];
   
  int main() {
      ios::sync_with_stdio(false);
      cin>>t;
       while(t--){
           cin>>n;
           me(res,0,sizeof(res));
            for(int i=1;i<=n;++i){
                cin>>a[i];
                dp[i]=1;
                res[i][1]=1;
            }
            for(int i=1;i<=n;++i){
                for(int j=1;j<i;++j){
                    if(a[j]<a[i]){
                        dp[i]=max(dp[i],dp[j]+1);
                        res[i][dp[j]+1]=(res[i][dp[j]+1]+res[j][dp[j]])%mod;
                    }
                }
            }
            sort(dp+1,dp+1+n);
            ll cnt=0;
            for(int i=1;i<=n;++i){
                cnt=(cnt+res[i][dp[n]])%mod;
            }
            printf("%d %lld\n",dp[n],cnt);
       }
      return 0;
  }