广度优先搜索是用来查找图模型中边数最少的路径,但如果图模型是加权图——边上考虑权重,则需要用到狄克斯特拉算法找到两节点之间的最短路径了。
一、问题
找出加权图中起点到终点的耗时最短的路径。
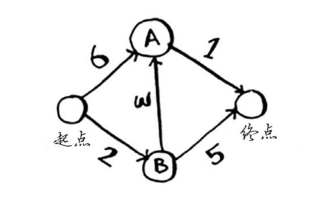
二、算法思路
1、找出从“起点”能前往的最“便宜”的邻节点;
2、算出邻节点的总开销;
3、将该开销更新到开销表;
4、重复前面三步,直到每一个节点都这样做了;
5、计算最终路径。
算法需要一个用于储存所有节点的邻节点以及到邻节点的花费的表,一个储存从起点到节点的总开销的开销表,一个储存父节点的表,这三个表都可以用散列表实现。
三、解题思路
1、准备:
(1)创建一个有每个节点以及其邻节点和该邻节点边上权重的散列表;
(2)创建一个从起点到各节点的最低开销表,该开销表会慢慢更新;
(3)创建储存父节点的表,当一个节点的最低开销发生变化,更新父节点。
2、算法思路:
(1)从开销表找出最便宜的节点;
(2)计算该节点的邻节点的总开销,即从起点到邻节点的总花费,
(3)用邻节点的总开销与开销表的比较。如果存在比原来便宜的节点,在开销表和父节点表更新它;如果存在每出现过的节点,在开销表和父节点表加上;
(4)标记该节点为已处理;
(5)重复前面4步,直到每一个节点都处理过。
3、代码示例:

