一、分而治之
分而治之(divide and conquer,DnC)是一种解决问题的思路,它的核心就是利用递归函数,不断把一个问题变成越来越小的问题,直到出现解决条件为止的解题思路。
二、分而治之解题实例
1、问题:假如你是一个农场主,你有一块1680×680的土地,现要求你将土地划分成均匀的方块,且方块的面积尽可能大,现求出最大的方块边长。
分而治之:分而治之解决问题的过程包括两个步骤:①找到最简单的情况(基础条件);②不断缩小问题的规模。
分析:由于原土地是一个矩形,所以最简单的情况是,该矩形能够分成两个以短边为边长的方形。但明显目前的矩形不符合这个条件。于是我们可以分出两个边长640的方形和一个640×400的矩形土地,这时我们就找到了缩小问题规模的方法了:每次都以短边为边长划分方形,剩下的矩形也用同样的方法划分,直到出现一个矩形它的长为宽的两倍为止。
欧几里得算法:

2、求出列表[2, 4, 6, 8, 10]的和,不能用for循环,不能用sum函数,算法能应用在任何一个数列。
第一步,找出最简单情况:最简单情况就是列表只有1个数,这样列表的和就等于这个数;
第二步,找出缩小问题规模的方法(递归函数):编写一个递归函数,每次都把列表的第一个数与剩下的其他数相加。
代码示例:

三、快速排序
快速排序是一种利用的DnC思路实现的排序方法,它的计算速度比选择排序快很多。
第一步,找出基础条件:当列表中只有1个数的时候;第二步,编写能够缩小问题规模的递归函数:每次都选择列表的第一个元素作为参考值,然后把小于参考值的数放在参考值左边的子列表,大于参考值的数放在参考值右边的子列表里,然后周而复始地对子列表运行快速排序。
代码示例:

注意,这里有一个陷阱,就是 if len(alist) < 2 这条if语句不能写成 if len(alist) == 1 ,因为如果pivot是列表中最大或者最小的数,greater或者less就是一个空列表。
四、快速排序的速度
每一层调用栈,记操作数为1,快速排序的调用栈的高度(操作数)最糟糕的情况是n,最好的情况是log2n。
而每一层调用栈中,要操作的元素每一层都会少一个,所以n层的平均时间是n/2。
所以快速排序最糟糕的情况是O(n)×O(n/2)=O(n2),常数部分对结果影响不大,舍去;最佳情况是O(log2n)×O(n/2)=O(n·log2n),同样舍去常数部分。但这里,最佳情况就是平均情况,所以快速排序的平均运行时间是O(n·logn)。
图例解释:
1、调用栈最糟糕情况:
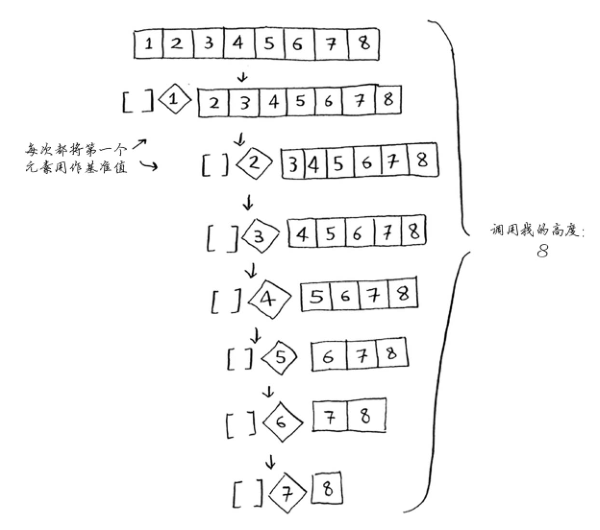
2、调用栈最佳情况:
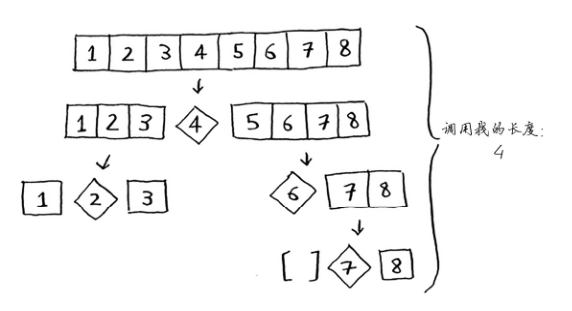
3、每一层调用栈操作数:(由于最后的常数部分都会舍去,所以这里每一层的操作数可简单认为都是n)
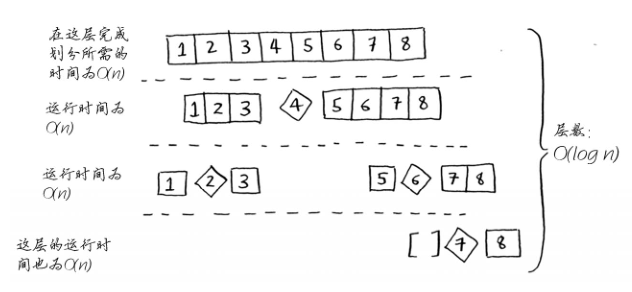
具体参考:《算法图解》第四章-快速排序
——————本篇完!