说起进制间的转换,可能除留取余法(我自己编的名字,没找到原来叫什么名字...)是用的最普遍的了,但是我们是否想过,使用得最普遍的方法的原理到底是什么呢?
就像下面这张图的进制转换,我们知道十进制1348转八进制,只要把他一直除8直至商为0,并且把最后的余数倒过来就是我们想要的结果了。
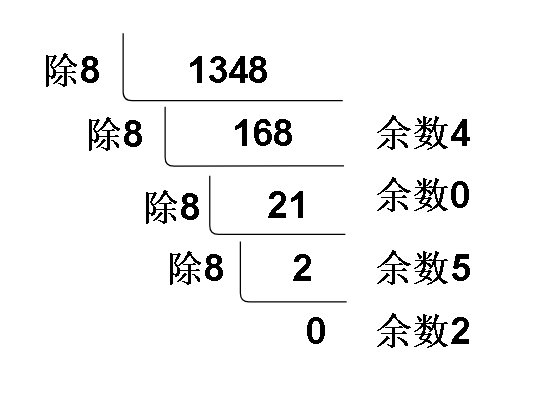
但为什么不去怀疑我们用的公式是不是正确的呢?合法性究竟在哪呢?
下面将证明上述方法的合法性
我们知道十进制数的权值分布是这样的:

那么我们先是很无聊地来做一次十进制到十进制的转换,也就是最后的结果是不变的,还是原来的十进制数,但是我们怎么得到各个位的数字呢?
请看以下过程:
如果我们同样采用除留取余法得到各个位的数字 :
首先 1348 % 10 = 8, 这表明什么呢?

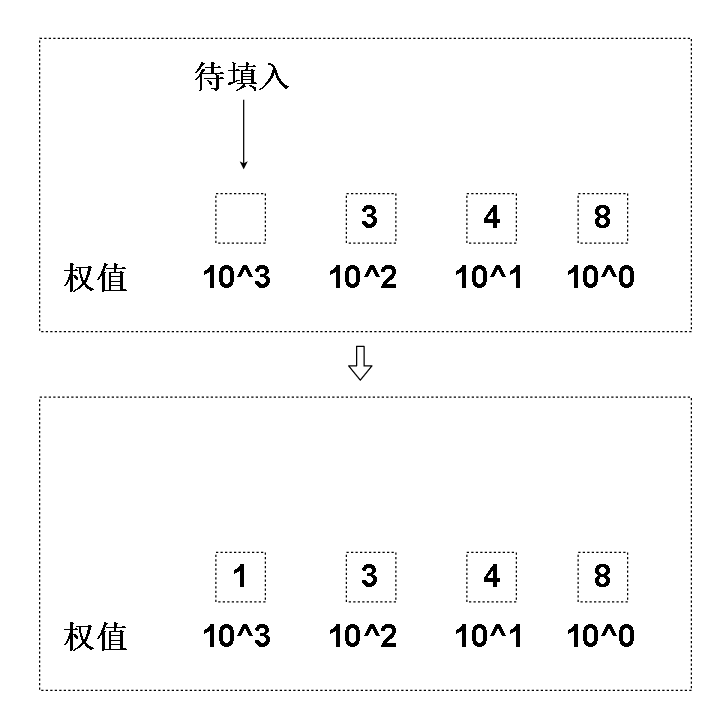
这说明我们的1348可以分成 134 个10^1 和 8 个 10^0,也就是134个10 和 8个1,这样我们就可以得到最低位个位上的数。
于是我们可以在个位上填入数字了
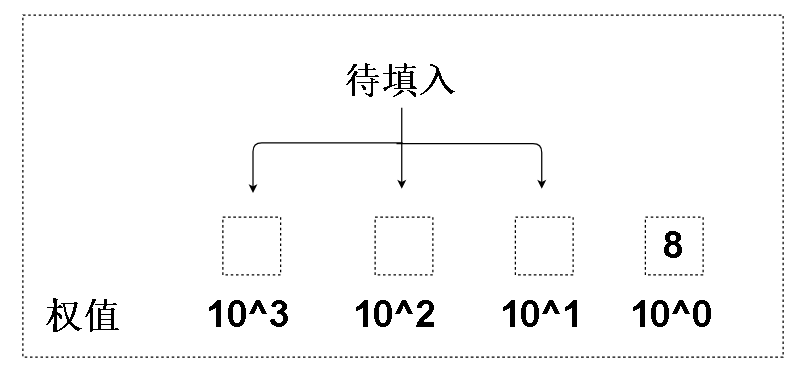
聪明的你可能已经发现了原理。如果没有的话不急,我们再做一步,你可能就看出来了。
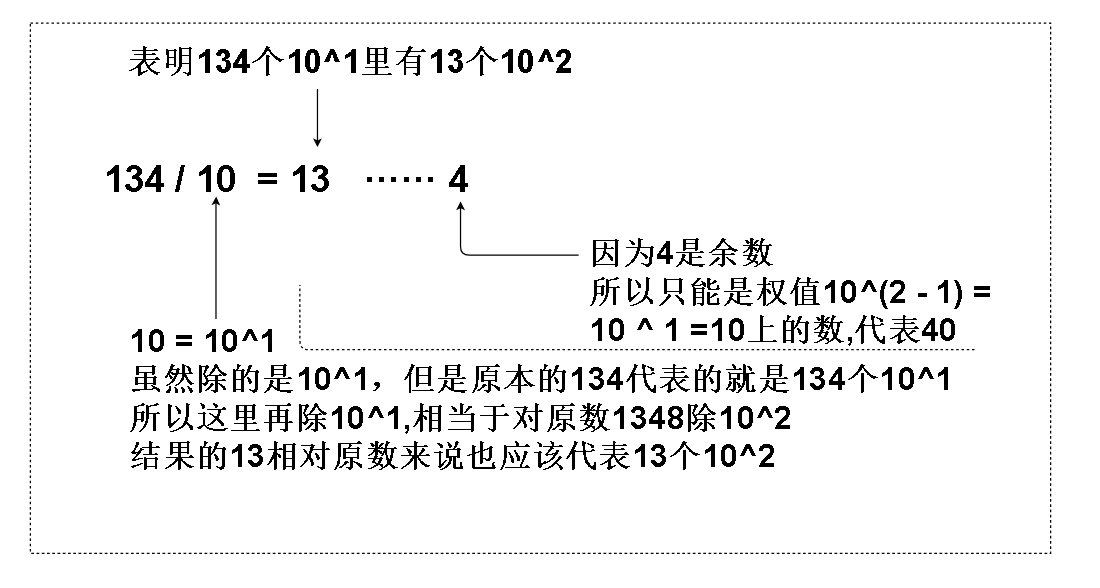
这时候我们可以得到 : 1348 是由 13个10^2 和 4个10^1 和 8个10^0 组成的,对应的,我们可以在10^1上填上4
因为13个10^2 里的13还不是一位数,所以我们不能把他填在10^2上。

那么该怎么处置13呢?再对他除10^1
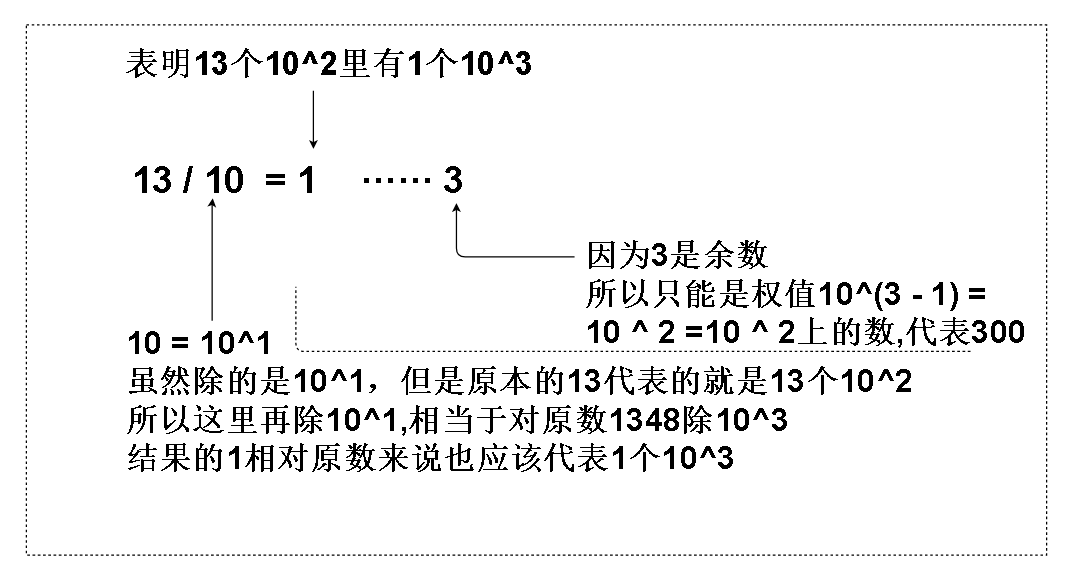
这时候我们就可填 10^2上的数字了,很明显是上图的3
而且因为我们的余数是1,已经是一位数了,代表1个10^3, 所以容易想到,这个1可以直接填在10^3的位置上
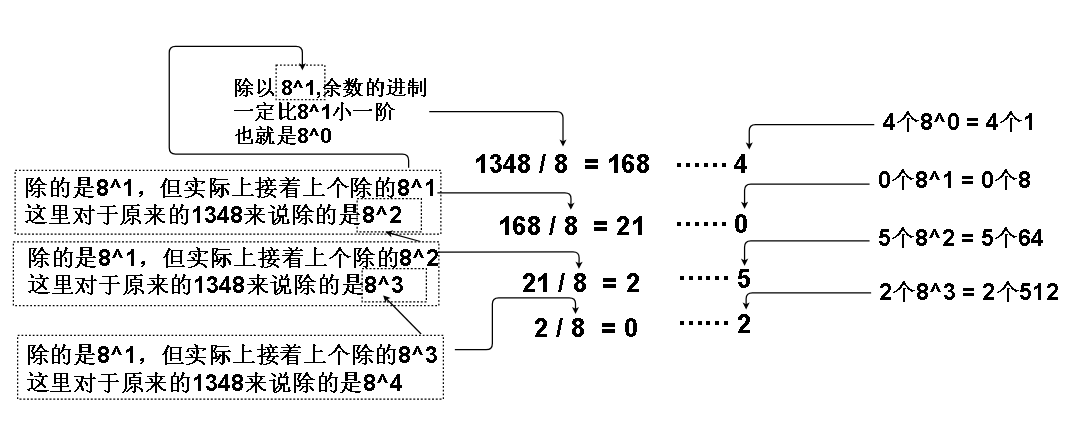
同理,我们把这种思想用到十进制转换成八进制上:

同理用在其他进制,比如在计算机界横行的二进制也一样。
我们观察到这种进制的转换,算出来的结果和我们要的最后数字是倒过来的,所以我们可以用栈这种结构来实现一下进制的转换。
首先我们实现一个简陋的栈结构 :
public class Stack{ private Object[] objects; private int top = -1; private static final int initialSize = 32; public Stack() { this.objects = new Object[initialSize]; } public <T> T pop(){ //<T>意味着我们可以根据需要选择返回的类型,不用每次获得都强转,虽然有类型转换错误的危险,但是这里是演示用,不做太严谨措施 if(top < 0){ return null; } return (T) objects[top --]; } public <T> T getTop(){ if(isEmpty()){ return null; } return (T) objects[top]; } public void push(Object o){ objects[++ top] = o; } public boolean isEmpty(){ return top == - 1; } }
具体实现 :
public String conversion(int source, int destinRadix){ StringBuilder builder = new StringBuilder(); Stack stack = new Stack(); while(source != 0){ //如下的运算比较低效,为了演示没有考虑效率 int left = source % destinRadix; source = (source - left) / destinRadix; stack.push(left); } while(!stack.isEmpty()){
//如果要转10进制以上的数请自行将10定义成a,11定义成b...... builder.append(stack.pop());
} return builder.toString(); }
测试:

