栈

栈

　　栈是一种只允许在序列末端操作的数据结构。栈的末端也称之为栈顶。 

　　栈的插入操作是将新元素压入栈顶，称为入栈。栈的删除操作是删除栈顶元素，称为出栈。由此可以看出，栈的特点是：后入栈的元素先出栈，先入栈的元素后出栈。

　　栈常用的操作有：入栈、出栈、取栈顶元素等。其接口定义如下：

public interface Stack<E> {

    void push(E e);

    E pop();

    E getTop();

    boolean isEmpty();

    int size();

    void clear();

}

顺序栈　　

　　顺序栈是采用顺序存储结构的栈。可以用一个数组来表示顺序栈，并指定栈顶位于数组末端。但是，数组的大小是预先确定的，存满之后无法继续插入新元素。所以在栈满时需要重新分配更大的空间进行扩容。

　　顺序栈中包括以下变量：

　　datas：存储元素的数组。

　　top：栈顶位标（栈顶元素的下一个位置）。top值也表示当前栈中的元素个数。

　　size：初始存储容量。

　　increment：数组扩容时增加的存储容量。

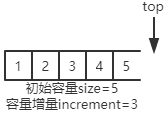
　　下图是一个初始容量为5，增量为3的栈：

　　

　　可以看到其中已经有4个元素，此时top=4表示下一个入栈的元素应该放在datas[4]位置。

入栈

　　入栈操作是将元素放入top指向的位置，然后top自增。

　　

　　可以看到，此时top的值为5，表示如果还有元素入栈，该元素需要放在datas[5]位置。而datas数组当前容量为5，并没有datas[5]位置，即不能再有新元素入栈，也就是栈已满。

　　所以，栈满的条件是：top指针的值等于datas数组当前容量，即top == datas.length。此时，如果再有元素入栈，需要先对栈进行扩容。因此，在每次入栈操作中，应该先判断栈是否需要扩容，之后再将元素压入栈中。

　　扩容操作可以理解为：重新定义一个datas数组，容量为原datas数组的容量加上容量增量increment，并将原datas数组中的所有元素放入新定义的datas数组中。

　　

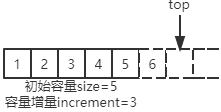
　　可以看到，扩容之后datas数组容量变为8，此时有了datas[5]位置，新元素可以入栈。

@SuppressWarnings("unchecked")
@Override
public void push(E e) {
    // top == datas.length表示栈满，需要扩容
    if (top == datas.length) {
        // 重新定义新的数组，容量为datas.length + increment
        E[] newbase = (E[]) new Object[datas.length + increment];
        // 将原datas数组中的元素复制进新的数组中
        System.arraycopy(datas, 0, newbase, 0, datas.length);
        // datas数组为新的数组
        datas = newbase;
    }
    // 将元素放入datas[top]中，并执行top++
    datas[top++] = e;
}

出栈

　　出栈操作是获取栈顶元素，并将栈顶位置置为null，最后让top自减。

　　

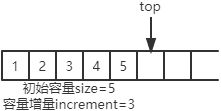
　　可以看到，原来的栈顶元素6被取出，top的值减1变为5，指向datas[5]位置。

@Override
public E pop() {
    // top自减，指向栈顶元素的位置，并获取栈顶元素
    E e = datas[--top];
    // 将当前位置置为null，表示栈顶元素被取出
    datas[top] = null;
    return e;
}

取栈顶元素

　　取栈顶元素仅仅是获取当前栈顶的元素，并没有将该元素弹出栈外。

　　

　　可以看到，当前的栈顶元素是5。

@Override
public E getTop() {
    return datas[top - 1];
}

获取当前栈中元素的个数

　　top的值除了表示下一个元素入栈的位置，还可以表示当前栈中元素的个数。

　　

　　当前top == 5，表示下一个元素入栈后存放的位置是datas[5]，也表示当前栈中有5个元素。

@Override
public int size() {
    return top;
}

判断栈是否为空

　　栈空的条件是：栈中元素的个数为0，即top == 0。

@Override
public boolean isEmpty() {
    return top == 0;
}

栈的应用

　　栈具有后进先出的特点，所以栈一般用于结果需要倒序输出，或者是匹配最近的单位等。

数制转换

　　十进制数转换成N进制数过程为：将十进制数除以n，得到商和余数；再继续将商除以n，得到下一个商和余数；直到商为0。最后将余数从低位到高位排列，即为转换后的结果。

　　例如将十进制数1348转换为八进制数：

　　1. 1348 ÷ 8 = 168 ...... 4

　　2. 168 ÷ 8 = 21 ...... 0

　　3. 21 ÷ 8 = 2 ...... 5

　　4. 2 ÷ 8 = 0 ...... 2

　　5. 得到的余数分别是4、0、5、2，从低位到高位排列，得到十进制数1348转换为八进制数的结果为2504。

　　可以看到得到的余数最终要倒序输出才得到最终结果，所以可以先用栈存储余数，之后将栈中的余数弹出，就得到倒序后的结果。

public static String convert(int n, int radix) {
    Stack<Integer> stack = new ArrayStack<Integer>();
    while (n != 0) {
        stack.push(n % radix);
        n /= radix;
    }
    String result = "";
    while (! stack.isEmpty()) {
        result += stack.pop();
    }
    return result;
}

　　输入n=1348，进制radix=8，得到结果为：

　　

括号匹配

　　假设括号序列中只允许出现括号（“(”、“)”、“[”、“]”、“{”、“}”），其出现的个数和顺序是任意的。对括号序列进行匹配，规则如下：

　　a. 如果为空串，返回true。

　　b. 如果当前右括号与前一个左括号不匹配（例如括号序列“([)]”，可以看到第一个出现的右括号是“)”，而前一个左括号是“[”，不匹配），返回false。

　　c. 右括号多余（例如括号序列“)[]”，右括号前没有左括号，是多余的），返回false。

　　d. 左右括号个数不一致（例如括号序列“([]”，左括号多余；括号序列“[])”，右括号多余），返回false。

　　可以用栈来实现该方法：

　　1. 从左向右扫描括号序列，若为左括号则压入栈中。若为右括号则先判断栈是否为空，为空表示当前右括号前没有左括号，表示右括号是多余的；不为空则弹出栈顶的左括号，判断是否与当前右括号匹配。

　　2. 扫描完括号序列后，判断栈是否已空，没有空表示左括号个数比右括号多，即存在多余的左括号，返回false。

public static boolean match(String str) {
    // 空串直接返回true
    if (str.equals("")) return true;
    Stack<Character> stack = new ArrayStack<Character>();
    for (int i = 0; i < str.length(); i++) {
        char c = str.charAt(i);
        if (c == '(' || c == '[' || c == '{') {   // 左括号直接入栈
            stack.push(c);
        } else if (c == ')') {   
            // 先判断栈是否为空，为空表示该“)”多余。不为空则弹出栈顶的左括号，判断是否为“("，不为“(”表示括号不匹配
            if (stack.isEmpty() || stack.pop() != '(') return false;
        } else if (c == ']') {
            // 先判断栈是否为空，为空表示该“]”多余。不为空则弹出栈顶的左括号，判断是否为“["，不为“[”表示括号不匹配
            if (stack.isEmpty() || stack.pop() != '[') return false;
        } else {
            // 先判断栈是否为空，为空表示该“}”多余。不为空则弹出栈顶的左括号，判断是否为“{"，不为“{”表示括号不匹配
            if (stack.isEmpty() || stack.pop() != '{') return false;
        }
    }
    // 判断栈是否为空，不为空表示左括号个数比右括号多，存在多余的左括号
    return stack.isEmpty();
}

　　

计算器

　　实现一个计算器功能，首先需要让计算器能够“读懂”输入的表达式。

　　算术表达式的表示形式按运算符的位置分，可以分为三种：中缀表达式、前缀表达式、后缀表达式。

　　计算器程序通过扫描算术表达式得到运算数、运算符，以及运算的先后顺序。通常情况下会借助一个数栈和一个符号栈实现。

中缀表达式

　　中缀表达式是指运算符位于运算数之间的表示形式。

　　计算器扫描中缀表达式计算结果的过程为：

　　1. 从左往右扫描中缀表达式：

　　　　a. 如果是数字，压入数栈。

　　　　b. 如果是运算符：如果符号栈为空，则直接将当前运算符压入符号栈。否则：如果符号栈栈顶符号不为“(”，且其优先级不低于当前运算符，则弹出栈顶运算符op，从数栈中依次弹出两个数，先弹出的为num2，后弹出的为num1，执行num1 op num2并将结果压入数栈。循环执行该操作直到符号栈为空或者栈顶符号为“(”或其优先级低于当前运算符。将当前运算符压入符号栈中。

　　　　c. 如果是“(”，压入符号栈中。

　　　　d. 如果是“)”，则弹出栈顶符号op。如果op不为“(”，则从数栈中依次弹出两个数，先弹出的为num2，后弹出的为num1，执行num1 op num2并将结果压入数栈，继续弹出下一个栈顶符号。循环执行该操作直到op为“(”。

　　2. 中缀表达式扫描完后，若符号栈不为空，则弹出栈顶符号op，从数栈中依次弹出两个数，先弹出的为num2，后弹出的为num1，执行num1 op num2并将结果压入数栈，继续弹出下一个栈顶符号。循环执行该操作直到符号栈为空。

　　3. 符号栈为空后，数栈只剩下一个元素，即为最终结果。弹出该元素即可。

　　例如，对于10 * ( 1 + 3 - 4 + 1 )：

　　1. 定义数栈和符号栈。

　　2. 扫描中缀表达式：

序号	描述	数栈	符号栈
a	扫描到“10”，直接压入数栈	[10	[
b	扫描到“*”，当前符号栈为空，直接压入符号栈	[10	[*
c	扫描到“(”，直接压入符号栈	[10	[*, (
d	扫描到“1”，直接压入数栈	[10, 1	[*, (
e	扫描到“+”，符号栈的栈顶符号为“(”，直接压入符号栈	[10, 1	[*, (, +
f	扫描到“3”，直接压入数栈	[10, 1, 3	[*, (, +
g	扫描到“-”： 1. 符号栈的栈顶符号为“+”，弹出栈顶符号“+”，数栈依次弹出“3”和“1”，执行“1 + 3”，将结果“4”压入数栈 2.  符号栈的栈顶符号为“(”，结束循环 3. 将“-”压入符号栈	[10, 4	[*, (, -
h	扫描到“4”，直接压入数栈	[10, 4, 4	[*, (, -
i	扫描到“+”： 1. 符号栈的栈顶符号为“-”，弹出栈顶符号“-”，数栈依次弹出“4”和“4”，执行“4 - 4”，将结果“0”压入数栈 2.  符号栈的栈顶符号为“(”，结束循环 3. 将“+”压入符号栈	[10, 0	[*, (, +
j	扫描到“1”，直接压入数栈	[10, 0, 1	[*, (, +
k	扫描到“)”： 1. 弹出栈顶符号“+” 2. 当前符号不是“(”，所以数栈依次弹出“1”和“0”，执行“0 + 1”，将结果“1”压入数栈，弹出下一个栈顶符号“(” 3. 当前符号是“(”，结束循环	[10, 1	[*

　　3. 符号栈不为空，需要依次弹出并进行运算：

序号	描述	数栈	符号栈
a	符号栈不为空，弹出栈顶符号“*”，数栈依次弹出“1”和“10”，执行“10 * 1”，将结果“10”压入数栈	[10	[

　　4. 弹出数栈最后一个元素“10”，即为运算的最终结果。

public static int calculateInfix(String infix) {
    Stack<Integer> numStack = new ArrayStack<Integer>();
    Stack<Operator> opStack = new ArrayStack<Operator>();
    int num1, num2;
    Operator op;
    for (String s : infix.split(" ")) {
        if (s.equals("+") || s.equals("-")) {
            while (! opStack.isEmpty()) {
                // +、-的优先级最低，所以如果栈顶符号不为“(”，都需要进行运算
                if (opStack.getTop() == Operator.left) break;
                // 弹出栈顶符号
                op = opStack.pop();
                // 先弹出的数为num2
                num2 = numStack.pop();
                // 后弹出的数为num1
                num1 = numStack.pop();
                // 执行num1 op num2，并将结果压入数栈
                numStack.push(calculate(num1, op, num2));
            }
            opStack.push(Operator.parse(s));
        } else if (s.equals("*") || s.equals("/")) {
            while (! opStack.isEmpty()) {
                op = opStack.getTop();
                // *、/的优先级高于+、-，所以如果栈顶符号不为“(”、“+”、“-”，都需要进行运算
                if (op == Operator.left || op == Operator.add || op == Operator.subtract) break;
                // 弹出栈顶符号
                op = opStack.pop();
                // 先弹出的数为num2
                num2 = numStack.pop();
                // 后弹出的数为num1
                num1 = numStack.pop();
                // 执行num1 op num2，并将结果压入数栈
                numStack.push(calculate(num1, op, num2));
            }
            opStack.push(Operator.parse(s));
        } else if (s.equals("(")) {
            // “(”直接压入符号栈
            opStack.push(Operator.left);
        } else if (s.equals(")")) {
            // 弹出栈顶符号
            op = opStack.pop();
            while (op != Operator.left) {
                // 先弹出的数为num2
                num2 = numStack.pop();
                // 后弹出的数为num1
                num1 = numStack.pop();
                // 执行num1 op num2，并将结果压入数栈
                numStack.push(calculate(num1, op, num2));
                // 弹出下一个栈顶符号
                op = opStack.pop();
            }
        } else {
            // 数字直接压入数栈
            numStack.push(Integer.parseInt(s));
        }
    }
    while (! opStack.isEmpty()) {
        // 弹出栈顶符号
        op = opStack.pop();
        // 先弹出的数为num2
        num2 = numStack.pop();
        // 后弹出的数为num1
        num1 = numStack.pop();
        // 执行num1 op num2，并将结果压入数栈
        numStack.push(calculate(num1, op, num2));
    }
    // 符号栈为空时，数栈只剩下一个元素，即为最终结果
    return numStack.pop();
}

前缀表达式

　　前缀表达式也叫做波兰表达式，是指运算符在运算数之前的表示形式。

　　计算器扫描前缀表达式计算结果的过程为：

　　1. 从右往左扫描前缀表达式：

　　　　a. 如果是数字，直接压入数栈。

　　　　b. 如果是运算符op，从数栈中弹出两个数，先弹出的数是num1，后弹出的数是num2，执行num1 op num2并将结果压入数栈。

　　2. 前缀表达式扫描完后，数栈只剩下一个元素，即为最终结果。弹出该元素即可。

　　例如，对于* 10 + - + 1 3 4 1：

　　1. 定义数栈。

　　2. 扫描前缀表达式：

序号	描述	数栈
a	扫描到“1”，直接压入数栈	[1
b	扫描到“4”，直接压入数栈	[1, 4
c	扫描到“3”，直接压入数栈	[1, 4, 3
d	扫描到“1”，直接压入数栈	[1, 4, 3, 1
e	扫描到“+”，数栈依次弹出“1”和“3”，执行“1 + 3”，将结果“4”压入数栈	[1, 4, 4
f	扫描到“-”，数栈依次弹出“4”和“4”，执行“4 - 4”，将结果“0”压入数栈	[1, 0
g	扫描到“+”，数栈依次弹出“0”和“1”，执行“0 + 1”，将结果“1”压入数栈	[1
h	扫描到“10”，直接压入数栈	[1, 10
i	扫描到“*”，数栈依次弹出“10”和“1”，执行“10 * 1”，将结果“10”压入数栈	[10

　　3. 弹出数栈最后一个元素“10”，即为运算的最终结果。

public static int calculatePrefix(String prefix) {
    Stack<Integer> numStack = new ArrayStack<Integer>();
    int num1, num2;
    Operator op;
    String[] strs = prefix.split(" ");
    for (int i = strs.length - 1; i >= 0; i--) {
        if (strs[i].equals("+") || strs[i].equals("-") || strs[i].equals("*") || strs[i].equals("/")) {   // 如果扫描到运算符
            op = Operator.parse(strs[i]);
            // 弹出的第一个数是num1
            num1 = numStack.pop();
            // 弹出的第二个数是num2
            num2 = numStack.pop();
            // 执行num1 op num2
            numStack.push(calculate(num1, op, num2));
        } else {
            // 直接将数字压入数栈
            numStack.push(Integer.parseInt(strs[i]));
        }
    }
    // 数栈中只有一个元素，即为最终结果
    return numStack.pop();
}

中缀表达式转为前缀表达式

　　中缀表达式转为前缀表达式的过程为：

　　1. 从右往左扫描中缀表达式：

　　　　a. 如果为数字，直接压入数栈。

　　　　b. 如果为运算符：

　　　　　　b1. 若符号栈为空，直接压入符号栈。

　　　　　　b2. 若符号栈不为空，栈顶符号不为“)”，且其优先级低于当前运算符，则弹出栈顶符号并压入数栈。循环该操作直到栈为空，或者栈顶符号为“)”或优先级不低于当前运算符的符号。最后把当前运算符压入符号栈。

　　　　c. 如果为“)”，直接压入符号栈。

　　　　d. 如果为“(”，依次弹出符号栈栈顶符号，如果是运算符就压入数栈，并弹出下一个栈顶符号，直到栈空或弹出的符号是“)”为止。

　　2. 中缀表达式扫描完后，依次弹出符号栈栈顶符号并压入数栈，直到栈空为止。

　　3. 将数栈中的元素倒序输出，即为前缀表达式。

　　例如，将10 * ( 1 + 3 - 4 + 1 )转为前缀表达式：

　　1. 定义数栈和符号栈。

　　2. 从右往左扫描中缀表达式：

序号	描述	数栈	符号栈
a	扫描到“)”，直接压入符号栈	[	[)
b	扫描到“1”，直接压入数栈	[1	[)
c	扫描到“+”，栈顶符号是“)”，直接压入符号栈	[1	[), +
d	扫描到“4”，直接压入数栈	[1, 4	[), +
e	扫描到“-”，栈顶符号是“+”，直接压入符号栈	[1, 4	[), +, -
f	扫描到“3”，直接压入数栈	[1, 4, 3	[), +, -
g	扫描到“+”，栈顶符号是“-”，直接压入符号栈	[1, 4, 3	[), +, -, +
h	扫描到“1”，直接压入数栈	[1, 4, 3, 1	[), +, -, +
i	扫描到“(”： 1. 弹出栈顶符号“+” 2. 当前符号不是“)”，压入数栈，弹出下一个栈顶符号“-” 3. 当前符号不是“)”，压入数栈，弹出下一个栈顶符号“+” 4. 当前符号不是“)”，压入数栈，弹出下一个栈顶符号“)” 5. 当前符号是“)”，结束循环	[1, 4, 3, 1, +, -, +	[
j	扫描到“*”，当前符号栈空，直接压入符号栈	[1, 4, 3, 1, +, -, +	[*
k	扫描到“10”，直接压入数栈	[1, 4, 3, 1, +, -, +, 10	[*

　　3. 符号栈不为空，依次弹出符号栈栈顶符号并压入数栈，最终得到数栈为：[1, 4, 3, 1, +, -, +, 10, *。

　　4. 将数栈中的元素倒序输出，得到结果“* 10 + - + 1 3 4 1”，即为前缀表达式。

public static String changeInfix2Prefix(String infix) {
    Stack<Operator> opStack = new ArrayStack<Operator>();
    Operator op;
    String[] strs = infix.split(" ");
    Stack<String> stack = new ArrayStack<String>();
    for (int i = strs.length - 1; i >= 0; i--) {
        if (strs[i].equals("+") || strs[i].equals("-")) {
            // +、-符号优先级最低，直接压入符号栈
            opStack.push(Operator.parse(strs[i]));
        } else if (strs[i].equals("*") || strs[i].equals("/")) {
            while (! opStack.isEmpty()) {
                op = opStack.getTop();
                if (op != Operator.add || op != Operator.subtract) break;
                // 如果符号栈栈顶符号是+、-，就弹出栈顶符号并压入数栈继续判断下一个栈顶符号
                stack.push(opStack.pop().toString());
            }
            // 将当前运算符压入符号栈
            opStack.push(Operator.parse(strs[i]));
        } else if (strs[i].equals("(")) {
            op = opStack.pop();
            // 直到符号栈空或弹出的符号为“)”为止，把弹出的符号压入数栈
            while (! opStack.isEmpty() && op != Operator.right) {
                stack.push(op.toString());
                op = opStack.pop();
            }
        } else if (strs[i].equals(")")) {
            // “)”直接压入符号栈
            opStack.push(Operator.right);
        } else {
            // 数字直接压入数栈
            stack.push(strs[i]);
        }
    }
    // 依次弹出符号栈中的元素并压入数栈
    while (! opStack.isEmpty()) {
        stack.push(opStack.pop().toString());
    }
    // 倒序输出数栈的元素
    String prefix = "";
    while (! stack.isEmpty()) {
        prefix += stack.pop() + " ";
    }
    prefix = prefix.substring(0, prefix.length() - 1);
    return prefix;
}

后缀表达式

　　后缀表达式也叫做逆波兰表达式，是指运算符在运算数之后的表示形式。

　　计算器扫描后缀表达式计算结果的过程为：

　　1. 从左往右扫描后缀表达式：

　　　　a. 如果是数字，直接压入数栈。

　　　　b. 如果是运算符op，从数栈中弹出两个数，先弹出的数是num2，后弹出的数是num1，执行num1 op num2并将结果压入数栈。

　　2. 后缀表达式扫描完后，数栈只剩下一个元素，即为最终结果。弹出该元素即可。

　　例如，对于10 1 3 + 4 - 1 + *：

　　1. 定义数栈。

　　2. 从左往右扫描后缀表达式：

序号	描述	数栈
a	扫描到“10”，直接压入数栈	[10
b	扫描到“1”，直接压入数栈	[10, 1
c	扫描到“3”，直接压入数栈	[10, 1, 3
d	扫描到“+”，数栈依次弹出“3”和“1”，执行“1 + 3”，将结果“4”压入数栈	[10, 4
e	扫描到“4”，直接压入数栈	[10, 4, 4
f	扫描到“-”，数栈依次弹出“4”和“4”，执行“4 - 4”，将结果“0”压入数栈	[10, 0
g	扫描到“1”，直接压入数栈	[10, 0, 1
h	扫描到“+”，数栈依次弹出“1”和“0”，执行“0 + 1”，将结果“1”压入数栈	[10, 1
i	扫描到“*”，数栈依次弹出“1”和“10”，执行“10 * 1”，将结果“10”压入数栈	[10

　　3. 弹出数栈最后一个元素“10”，即为运算结果。

public static int calculateSuffix(String suffix) {
    Stack<Integer> numStack = new ArrayStack<Integer>();
    int num1, num2;
    Operator op;
    String[] strs = suffix.split(" ");
    for (int i = 0; i < strs.length; i++) {
        if (strs[i].equals("+") || strs[i].equals("-") || strs[i].equals("*") || strs[i].equals("/")) {
            op = Operator.parse(strs[i]);
            // 先弹出的数是num2
            num2 = numStack.pop();
            // 后弹出的数是num1
            num1 = numStack.pop();
            // 执行num1 op num2，并将结果压入数栈
            numStack.push(calculate(num1, op, num2));
        } else {
            // 数字直接压入数栈
            numStack.push(Integer.parseInt(strs[i]));
        }
    }
    // 数栈只剩下一个元素，即为最终结果
    return numStack.pop();
}

中缀表达式转为后缀表达式

　　中缀表达式转为后缀表达式的过程为：

　　1. 从左往右扫描中缀表达式：

　　　　a. 如果为数字，直接压入数栈。

　　　　b. 如果为运算符：

　　　　　　b1. 若符号栈为空，直接压入符号栈。

　　　　　　b2. 若符号栈不为空，栈顶符号不为“(”，且其优先级不高于当前运算符，则弹出栈顶符号并压入数栈。循环该操作直到栈为空，或者栈顶符号为“(”或优先级高于当前运算符的符号。最后把当前运算符压入符号栈。

　　　　c. 如果为“(”，直接压入符号栈。

　　　　d. 如果为“)”，依次弹出符号栈栈顶符号，如果是运算符就压入数栈，并弹出下一个栈顶符号，直到栈空或弹出的符号是“(”为止。

　　2. 中缀表达式扫描完后，依次弹出符号栈栈顶符号并压入数栈，直到栈空为止。

　　3. 将数栈中的元素正序输出，即为后缀表达式。

　　例如，将10 * ( 1 + 3 - 4 + 1 )转为后缀表达式：

　　1. 定义数栈和符号栈。

　　2. 从左往右扫描中缀表达式：

序号	描述	数栈	符号栈
a	扫描到“10”，直接压入数栈	[10	[
b	扫描到“*”，符号栈为空，直接压入符号栈	[10	[*
c	扫描到“(”，直接压入符号栈	[10	[*, (
d	扫描到“1”，直接压入数栈	[10, 1	[*, (
e	扫描到“+”，栈顶符号是“(”，直接压入符号栈	[10, 1	[*, (, +
f	扫描到“3”，直接压入数栈	[10, 1, 3	[*, (, +
g	扫描到“-”： 1. 栈顶符号是“+”，弹出栈顶符号并压入数栈 2. 栈顶符号是“(”，结束循环 3. 将“-”压入符号栈	[10, 1, 3, +	[*, (, -
h	扫描到“4”，直接压入数栈	[10, 1, 3, +, 4	[*, (, -
i	扫描到“+”： 1. 栈顶符号是“-”，弹出栈顶符号并压入数栈 2. 栈顶符号是“(”，结束循环 3. 将“+”压入符号栈	[10, 1, 3, +, 4, -	[*, (, +
j	扫描到“1”，直接压入数栈	[10, 1, 3, +, 4, -, 1	[*, (, +
k	扫描到“)”： 1. 弹出栈顶符号“+” 2. 当前符号不是“(”，压入数栈，弹出下一个栈顶符号“(” 3. 当前符号是“(”，结束循环	[10, 1, 3, +, 4, -, 1, +	[*

　　3. 符号栈不为空，依次弹出符号栈栈顶符号并压入数栈，最终得到数栈为：[10, 1, 3, +, 4, -, 1, +, *。

　　4. 将数栈中的元素正序输出，得到结果“10 1 3 + 4 - 1 + *”，即为后缀表达式。

public static String changeInfix2Suffix(String infix) {
    Stack<Operator> opStack = new ArrayStack<Operator>();
    Operator op;
    String[] strs = infix.split(" ");
    Stack<String> stack = new ArrayStack<String>();
    for (int i = 0; i < strs.length; i++) {
        if (strs[i].equals("+") || strs[i].equals("-")) {
            while (! opStack.isEmpty()) {
                op = opStack.getTop();
                // +、-优先级最低，所以如果不是+、-直接结束循环
                if (op != Operator.add && op != Operator.subtract) break;
                stack.push(opStack.pop().toString());
            }
            opStack.push(Operator.parse(strs[i]));
        } else if (strs[i].equals("*") || strs[i].equals("/")) {
            while (! opStack.isEmpty()) {
                // *、/优先级最高，所以如果是“(”直接结束循环
                if (opStack.getTop() == Operator.left) break;
                stack.push(opStack.pop().toString());
            }
            // 当前运算符压入符号栈
            opStack.push(Operator.parse(strs[i]));
        } else if (strs[i].equals("(")) {
            // “(”直接压入符号栈
            opStack.push(Operator.left);
        } else if (strs[i].equals(")")) {
            // 弹出栈顶符号
            op = opStack.pop();
            while (! opStack.isEmpty() && op != Operator.left) {
                // 如果是运算符则压入数栈
                stack.push(op.toString());
                // 弹出下一个栈顶符号
                op = opStack.pop();
            }
        } else {
            // 数字直接压入数栈
            stack.push(strs[i]);
        }
    }
    // 符号栈中剩下的元素依次弹出并压入数栈
    while (! opStack.isEmpty()) {
        stack.push(opStack.pop().toString());
    }
    // 数栈正序输出即为后缀表达式
    String suffix = stack.toString();
    suffix = suffix.substring(1, suffix.length() - 1);
    return suffix;
}