前言:
对于线性回归问题,通常有两种方法可以解决,即梯度下降法和标准方程法,两者各有优缺点
梯度下降法对于参数多的回归方程仍然适用,但并不是每次都能达到最优解,神经网络也需要梯度下降法来解决
标准方程法适用于参数少的回归方程,但是时间复杂度较高
正文:
首先来看一下梯度下降法的代码
import numpy as np
import matplotlib.pyplot as plt
#这两个数据库是经常在机器学习中使用的,numpy通常用于科学计算等
#matplotlib是画图工具,简写为np和plt
#载入数据
data = np.genfromtxt("data.csv",delimiter=",")
#使用genfromtxt函数载入data数据,使用逗号","来进行数据分隔
x_data = data[:,0]
#将数据进行切割,x轴的数据取每一行的第一列
y_data = data[:,1]
#将数据进行切割,y轴的数据取每一行的第二列
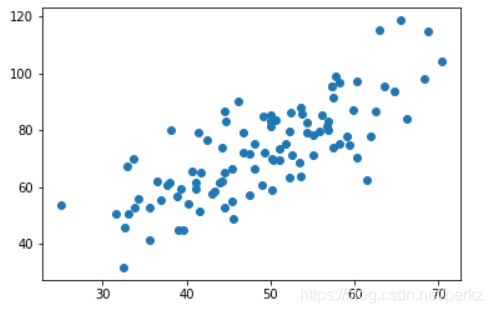
plt.scatter(x_data,y_data)
#使用scatter函数进行描点
plt.show()
#展示描点结果
展示结果如下:
#学习率,学习率越大步长越大,越小步长也越小
lr=0.0001
#截距
b=0
#斜率
k=0
#最大迭代次数
epochs = 50
#最小二乘法
def compute_error(b,k,x_data,y_data):#定义了4个参数
totalError = 0
for i in range(0,len(x_data)):
totalError+=(y_data[i]-(k*x_data[i]+b))**2
#这一步在计算j(theta)的值
return totalError/float(len(x_data))/2.0
def gradient_descent_runner(x_data,y_data,b,k,lr,epochs):
#算出一共有多少个数据
m=float(len(x_data))
#循环epochs次来进行训练
for i in range(epochs):
b_grad = 0
k_grad = 0
#计算梯度的总和再求平均
for j in range(0,len(x_data)):
b_grad += (1/m)*(((k*x_data[j]) + b)-y_data[j]
k_grad += (1/m)*x_data[j]*(((k*x_data[j])+b)-y_data[j])
#以上两步都是求导后的结果,即对j(thta)进行求导
#求导过程就不展示了
#同步更新b和k
b=b-(lr*b_grad)
k=k-(lr*k_grad)
#下面这一步是为了展示更新过程,如果不需要也可以注释掉
if i%5==0:
print("epochs:",i)
plt.plot(x_data,y_data,'b.')
plt.plot(x_data,k*x_data + b,'r')
plt.show()
return b,k
#下面操作利用format(格式化)函数来打印出结果
print("strating b={0},k={1},error = {2}".format(b,k,compute_error(b,k,x_data,y_data)))
#打印一元线性回归的参数初始值
print("running...")
#调用更新函数进行同步更新,并将b,k的值弄好
b,k=gradient_descent_runner(x_data,y_data,b,k,lr,epochs)
#打印出最终结果
print("After{0}iterations b = {1},k={2},error = {3}".format(epochs,b,k,compute_error(b,k,x_data,y_data)))
#画图
plt.plot(x_data,y_data,'b.')
plt.plot(x_data,k*x_data + b,'r')
plt.show()
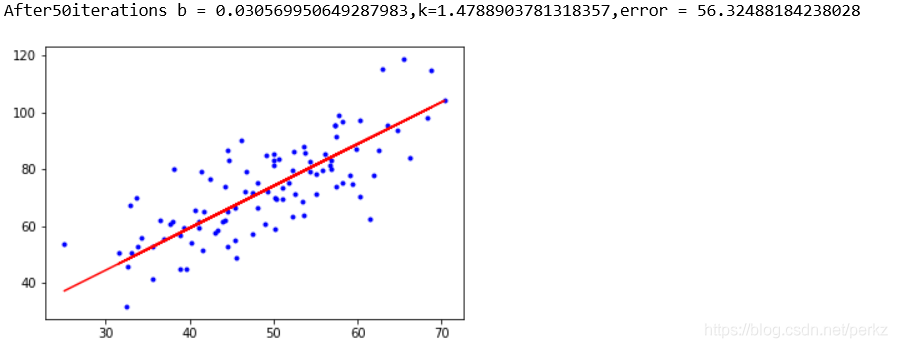
最后的效果还是比较满意!