10折交叉验证
我们构建一个分类器,输入为运动员的身高、体重,输出为其从事的体育项目-体操、田径或篮球。
一旦构建了分类器,我们就可能有兴趣回答类似下述的问题:
1. 该分类器的精确率怎么样? 2. 该分类器到底有多好? 3. 和其他分类器相比较,该分类器表现如何?
我们把每个数据集分成两个子集 - 一个用于构建分类器,该数据集称为训练集(training set) - 另一个数据集用于评估分类器,该数据集称为测试集(test set) 训练集和测试集是数据挖掘中的常用术语。 下面以近邻算法为例来解释为什么不能使用训练数据来测试。如果上述例子中的篮球运动员Marissa Coleman在训练数据中存在,那么身高6英尺1英寸体重160磅的她就会与自己最近。因此,如果对近邻算法进行评估时,若测试集是训练数据的子集,那么精确率总是接近于100%。更一般地,在评估任意数据挖掘算法时,如果测试集是训练数据的子集,那么结果就会十分乐观并且过度乐观。因此,这种做法看起来并不好。 那么我们将数据集分成两部分。较大的那部分用于训练,较小的那部分用于评估。事实表明这种做法也存在问题。在进行数据划分时可能会极端不走运。例如,所有测试集中的篮球运动员都比较矮(像Debbie Black的身高只有5英尺3英寸,体重只有124磅),他们会被分成马拉松运动员。而测试集中所有的田径运动员就像Tatyana Petrova(俄罗斯马拉松运动员,身高5英尺3英寸,体重108磅)一样较矮、体重较轻,可能会被分成体操运动员。如果测试集像上面一样,分类器的精确率会很差。另一方面,有时候测试集的选择又会十分幸运。测试集中的每个人都有所从事项目的标准身高和体重,此时分类器精确率接近100%。两种情况下,精确率都依赖于单个的测试集,并且该测试集可能并不能反映分类器应用于新数据的真实精确率。 上述问题的一种解决方法是重复多次上述过程并对结果求平均。例如,我们可以将数据分成两半:Part 1和Part 2。
我们可以使用Part 1的数据来训练分类器,而利用Part 2的数据对分类器进行测试。然后,我们重复上述过程,这次用Part 2训练而用Part 1测试。最后我们将两次的结果进行平均。但是,这种方法的问题在于我们每次只使用了一半数据进行训练。然而,我们可以通过增加划分的份数来解决这个问题。例如,我们可以将数据划分成3部分,每次利用2/3的数据训练而在其余1/3的数据上进行测试。因此,整个过程看起来如下:
第一次迭代 使用Part 1和Part 2训练,使用Part 3测试
第二次迭代 使用Part 1和Part 3训练,使用Part 2测试
第三次迭代 使用Part 2和Part 3训练,使用Part 1测试
对上述结果求平均。
在数据挖掘中,最常用的划分数目是10,这种方法称为……
10折交叉验证(10-fold Cross Validation)
使用这种方法,我们将数据集随机分成10份,使用其中9份进行训练而将另外1份用作测试。该过程可以重复10次,每次使用的测试数据不同。
10折交叉验证的例子
第1步,将数据等分到10个桶中。

我们会将50名篮球运动员和50名非篮球运动员分到每个桶中。每个桶当中放入了100人的信息。
第2步,下列步骤重复10次。
(1)每一次迭代中留存其中一个桶。第一次迭代中留存桶1,第二次留存桶2,其余依此类推。
(2)用其他9个桶的信息训练分类器(第一次迭代中利用从桶2到桶10的信息训练分类器)。
(3)利用留存的数据来测试分类器并保存测试结果。在上例中,这些结果可能如下:
35个篮球运动员被正确分类;
29个非篮球运动员被正确分类。
第3步,对上述结果汇总。
通常情况下我们会将结果放到与下表类似的表格中:
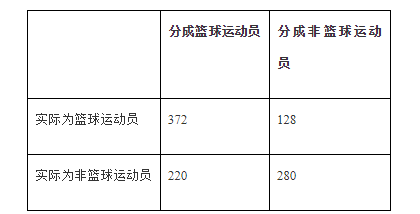
在所有500名篮球运动员中,有372人被正确分类。可能需要做的一件事是将右下角的数字也加上去,也就是说1000人当中有652(372+280)人被正确分类。因此得到的精确率为65.2%。与2折或3折交叉验证相比,基于10折交叉验证得到的结果可能更接近于分类器的真实性能。之所以这样,是因为每次采用90%而不是2折交叉验证中仅仅50%的数据来训练分类器。
有个问题 如果10折交叉验证之所以好只是因为采用了90%数据的话 那么为什么不用n折交叉验证?(n是数据集中样本的数目) 例如,如果数据集中包含1000个样本,我们可以在999个样本上训练分类器 然后在另外一个样本上测试分类器,这个过程可以重复1000次 利用这种最大可能的交叉验证次数,可能会得到更精确的分类器
留一法(Leave-One-Out)
在机器学习领域,n折交叉验证(n是数据集中样本的数目)被称为留一法。我们已经提到,留一法的一个优点是每次迭代中都使用了最大可能数目的样本来训练。另一个优点是该方法具有确定性。
确定性的含义
假设Lucy集中花费了80个小时来编写一个新分类器的代码。现在是周五,她已经筋疲力尽,于是她请她的两个同事(Emily和Li)在周末对分类器进行评估。她将分类器和相同的数据集交给每个人,请她们做10折交叉验证。周一,她问两人的结果……
嗯,她们得到了不同的结果。她们俩可能是谁犯错了吗?未必如此。在10折交叉验证中,我们随机将数据分到桶中。由于随机因素的存在,有可能Emily和Li的数据划分结果并不完全一致。实际上,她们划分一致的可能性微乎其微。因此,她们在训练分类器时,所用的训练数据并不一致,而在测试时所用的数据也不完全一致。因此,她们得到不同的结果是很符合逻辑的。该结果与是否由两个不同的人进行评估毫无关系。即使Lucy自己进行两次10折交叉验证,她得到的结果也会有些不同。之所以不同的原因在于将数据划分到桶这个过程具有随机性。由于10折交叉验证不能保证每次得到相同的结果,因此它是一种非确定性的方法。与此相反,留一法是确定性的。每次应用留一法到同一分类器及同一数据上,得到的结果都一样。这是件好事!
留一法的缺点
留一法的主要不足在于计算的开销很大。
考虑一个包含1000个实例的中等规模的数据集,需要一分钟来训练分类器。
对于10折交叉验证来说,我们将花费10分钟用于训练。而对于留一法来说,训练时间需要16个小时。
如果数据集包含百万样本,那么花费在训练上的总时间将接近两年。我的天哪!
留一法的另一个缺点与分层采样(stratification)有关。
分层采样(Stratification)
回到上一章的例子,即构建分类器来确定女运动员所从事的体育项目(篮球、体操或田径)。
当训练分类器时,我们希望训练数据能够具有代表性,并且包含所有3类的数据。
假设采用完全随机的方式将数据分配到训练集,则有可能训练集中不包含任何篮球运动员。
正因为如此,最终的分类器对篮球运动员分类时效果不佳。
或者,考虑构建一个100个运动员的数据集。
首先我们去WNBA的网站获得33个女子篮球运动员的信息,然后去维基百科网站获得33名参加2012年奥运会的女子体操运动员的信息,最后我们再次去维基百科网站获得34名参加奥运会田径项目的女运动员的信息。
因此,最终我们的数据如下所示:

下面开始做10折交叉验证。我们从上表的第一行开始,每10个人放入一个桶。 于是,第一个桶和第二个桶只有篮球运动员。第三个桶既有篮球运动员也有体操运动员。第四、第五个桶只包含体操运动员,其余桶的情况可以依此类推。 任何一个桶都不能代表整个数据集,你认为上述划分会导致有偏差的结果,这种想法是对的。 我们期望的方法是将实例按照其在整个数据集的相同比例分到各个桶中,即桶中的类别比例(篮球运动员、体操运动员、马拉松运动员)和整个数据集中的类别比例是一样的。 由于整个数据集的1/3是篮球运动员,因此每个桶中应该包含1/3的篮球运动员。同样,该桶中也应包含1/3的体操运动员和1/3的马拉松运动员。 上述做法称为分层采样,是一种好的方法。 留一法评估的问题在于测试集中只有一个样本,因此它肯定不是分层采样的结果。 总而言之,留一法可能适用于非常小的数据集,到目前为止10折交叉测试是最流行的选择。