题意翻译
题目大意
一开始有kk种生物,这种生物只能活1天,死的时候有p_ipi的概率产生ii只这种生物(也只能活一天),询问m天内所有生物都死的概率(包括m天前死亡的情况)
输入格式
第一行输入一个整数TT,表示数据总数
每一组先输入三个整数n(1<=n<=1000),k(0<=k<=1000),m(0<=m<=1000)n(1<=n<=1000),k(0<=k<=1000),m(0<=m<=1000)
然后输入n个整数,分别为p_0p0到p_{n-1}pn−1
输出格式
对于每一组数据,先输出"Case #x: " 再输出答案,精度要求在1e-6以内
感谢@xMinh 提供翻译
题目描述

输入输出格式
输入格式:
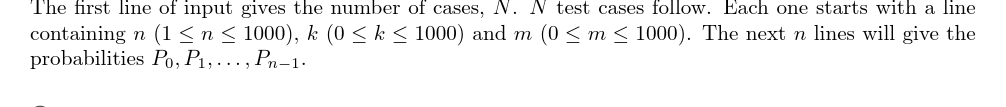
输出格式:

输入输出样例
输入样例#1: 复制
4 3 1 1 0.33 0.34 0.33 3 1 2 0.33 0.34 0.33 3 1 2 0.5 0.0 0.5 4 2 2 0.5 0.0 0.0 0.5
输出样例#1: 复制
Case #1: 0.3300000 Case #2: 0.4781370 Case #3: 0.6250000 Case #4: 0.3164062
//Pro:UVA11021 Tribles //每种麻球都是独立互不影响的,可以先算一种麻球 //对于一种麻球,有全概率公式计算, //令f[i]为麻球在前i天全部死亡的概率 //那么有f[i]=p0+p1*f[i-1]+p2*f[i-1]^2+...+pn*f[i-1]^n //最后的答案就是f[m]^k #include<iostream> #include<cstdio> #include<cstring> #include<cmath> #include<algorithm> using namespace std; const int N=1e3+5; int T,n,k,m; double f[N]; double p[N]; int cas; int main() { scanf("%d",&T); while(T--) { memset(f,0,sizeof(f)); scanf("%d%d%d",&n,&k,&m); for(int i=0;i<n;++i) scanf("%lf",p+i); f[0]=0,f[1]=p[0]; for(int i=2;i<=m;++i) { for(int j=0;j<n;++j) { f[i]+=p[j]*pow(f[i-1],j); } } printf("Case #%d: %.7lf ",++cas,pow(f[m],k)); } return 0; }