P1886 滑动窗口

题目描述

现在有一堆数字共N个数字（N<=10^6），以及一个大小为k的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

例如：

The array is [1 3 -1 -3 5 3 6 7], and k = 3.

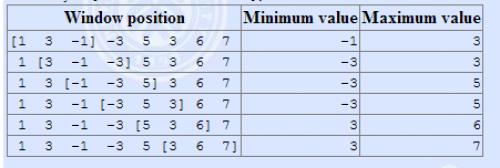
输入输出格式

输入格式：

输入一共有两行，第一行为n,k。

第二行为n个数(<INT_MAX).

输出格式：

输出共两行，第一行为每次窗口滑动的最小值

第二行为每次窗口滑动的最大值

输入输出样例

输入样例#1： 复制

8 3
1 3 -1 -3 5 3 6 7

输出样例#1： 复制

-1 -3 -3 -3 3 3
3 3 5 5 6 7

说明

50%的数据，n<=10^5

100%的数据，n<=10^6

/*维护一个下标递增、值也递增的队列。当扫描到第 i 个数时，将队头下标<=i-k的数删掉（把入队时间太长的给删掉，因为已经没有用了），同时将第 i个数插入，此时队头元素即为所求最小值。*/ 
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<string>
#include<algorithm>
#define N 1000005
using namespace std;

inline int read()
{
    int sum=0,f=1;char c=getchar();
    for(;(c<'0'||c>'9')&&c!='-';c=getchar());
    if(c=='-'){f=-1;c=getchar();}
    for(;c>='0'&&c<='9';c=getchar()){sum=sum*10+c-'0';}
    return sum*f;
}

int n,k,a[N];
int que[N],head,tail,id[N];    //que是单调队列，id是对应编号。

void mymin()
{
    head=1;
    tail=0;
    for(int i=1;i<=n;++i)
    {
        while(head<=tail&&que[tail]>=a[i]) tail--;    //只要队列里有元素，并且尾元素比待处理值大，即表示尾元素已经不可能出场，直到尾元素小于待处理值
        que[++tail]=a[i];        //待处理值入队
        id[tail]=i;        //存下其编号
        while(id[head]<=i-k) head++;    //如果队首元素已经"过时"，出队
        if(i>=k) printf("%d ",que[head]);//输出最值，即队首元素。i>=k输出
    }
    printf("
");
}

void mymax()    //找最大值，和最小值德操作反着 
{
    head=1;
    tail=0;
    for(int i=1;i<=n;++i)
    {
        while(head<=tail&&que[tail]<=a[i]) tail--;
        que[++tail]=a[i];
        id[tail]=i;
        while(id[head]<=i-k) head++;
        if(i>=k) printf("%d ",que[head]);
    }
    printf("
");
}

int main()
{
    n=read();k=read();
    for(int i=1;i<=n;++i)
    {
        a[i]=read();
    }
    mymin();
    mymax();
    return 0;
}

/*一开始写的线段树，TLE了最后一个点，讨论里说正解是模拟。。。这道题线段树并不难写，但是时间复杂度的原因会TLE。后来加了个特判，当k==1时按原样输出就过了。 */

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define N 1000005
using namespace std;

int n,k,maxn,minn;
int num[N],min_tree[N*4],max_tree[N*4];
int max_ans[N],min_ans[N];

void build(int root,int l,int r)
{
    if(l==r)    //找叶节点，对应原数组 
    {
        max_tree[root]=num[l];        //存当前子树中的最大值 
        min_tree[root]=num[l];        //存当前子树中的最小值 
        return;
    }
    int mid=(l+r)>>1;
    build(root<<1,l,mid);    //建左子树 
    build(root<<1|1,mid+1,r);    //建右子树 
    max_tree[root]=max(max_tree[root<<1],max_tree[root<<1|1]);    //求当前子树中的最大值 
    min_tree[root]=min(min_tree[root<<1],min_tree[root<<1|1]);    //求最小值 
}

void query(int root,int l,int r,int L,int R)
{
    if(L<=l&&r<=R)        //查询区间包含当前区间，直接调用当前区间的值 
    {
        maxn=max(maxn,max_tree[root]);    //最大的 
        minn=min(minn,min_tree[root]);    //最小的 
        return;
    }
    int mid=(l+r)>>1;
    if(L<=mid) query(root<<1,l,mid,L,R);    //找查询区间在线段树中的范围 
    if(mid<R) query(root<<1|1,mid+1,r,L,R);
}

int main()
{
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&num[i]);
    }
    if(k==1)    //k==1时按原样输出 
    {
        for(int i=1;i<=n;i++)
        {
            printf("%d ",num[i]);
        }
        printf("
");
        for(int i=1;i<=n;i++)
        {
            printf("%d ",num[i]);
        }
        return 0;
    }
    build(1,1,n);        //建树 
    for(int i=1;i<=n-k+1;i++)        //找窗口中能看到的最大最小值 
    {
        maxn=-999999999,minn=999999999;        //初始化 
        query(1,1,n,i,i+k-1);
        max_ans[i]=maxn;        // 
        min_ans[i]=minn;
    }
    for(int i=1;i<=n-k+1;i++)
    {
        printf("%d ",min_ans[i]);
    }
    printf("
");
    for(int i=1;i<=n-k+1;i++)
    {
        printf("%d ",max_ans[i]);
    }
    return 0;
}