一、最小路径覆盖：
给定有向图G=(V,E)。设P 是G 的一个简单路（顶点不相交、重复）的集合。如果V 中每个顶点恰好在P 的一条路上，则称P是G 的一个路径覆盖。P 中路径可以从V 的任何一个顶点开始，长度也是任意的，特别地，可以为0。G 的最小路径覆盖是G 的所含路径条数最少的路径覆盖。
性质：最小路径覆盖=|G|-最大匹配数
上述公式中最大匹配数是这样来的：
对于G中每一个节点x，建立节点x1，x2。若x- >y存在边，则x1与y2之间连一条无向边，求这个二分图的最大匹配数即可。
证明如下：
首先，若最大匹配数为0，则二分图中无边，也就是说有向图G中不存在边，那么
显然：最小路径覆盖=|G|-最大匹配数=|G|-0=|G|。
若此时增加一条匹配边x1--y2，则在有向图|G|中，x、y在同一条路径上，最小路径覆盖数减少一个。
继续增加匹配边，每增加一条，最小路径覆盖数减少一个，则公式：最小路径覆盖=|G|-最大匹配数得证。
二、最小点覆盖
点覆盖，在图论中点覆盖的概念定义如下：对于图G=(V,E)中的一个点覆盖是一个集合S⊆V使得每一条边至少有一个端点在S中。（摘自百度百科）
最小点覆盖就是说，选择最少的点去覆盖图中所有的边，
性质：最小点覆盖数 = 最大匹配数
证明：
首先，我们要抓住二分图最大匹配后图的特点，此时，不存在增广路。如下图所示，该图为不完整的最大匹配后的二分图：
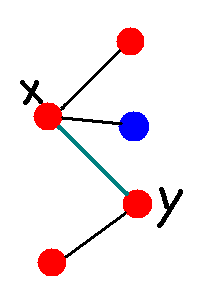
红点为匹配点，蓝点为未匹配点。
对于一个点而言，他所连接的点有这三种情况：
1、只连接了红点；
2、只连接了蓝点；
3、连接了红点和蓝点。
在上面的图中，x与y是所连接的边是匹配边。x连接了红点和蓝点，这个时候，y所连接的点一定没有蓝点，如果有，就是一条新的增广路，那么该图就不是最大匹配图了。
另一点更明显，就是在最大匹配图中 不会出现一条边同时连接着两个蓝点，因为两个连着两个蓝点的话这条边也是一个匹配。
那么，对于一条边而言，只有两种情况：
1、两端的点是红点；
2、两端的点一点是红色，一点是蓝色。
可知，一条边上，一定有红点，那么，我们就选择红点作为覆盖点。
对于上面的匹配边xy，我们无论是选择x还是y都可以覆盖xy这条边，但是对于图中的蓝点而言，只能选择x作为覆盖点去覆盖那条边，这样，我们就选择x作为覆盖点，它所覆盖的边中，既包括了与他相连的那些蓝点的边，也包括了xy这条匹配边。因为y点没有蓝色连接点，所以，y不是必须选择的覆盖点，它与那些红点相连的边都可以选择那些红点来覆盖边。所以，对于一条匹配边而言，我们只需要选择其中一个点就可以覆盖完整个二分图里的边了。
所以最小覆盖点数等于最大匹配。
三、最大独立点集
最大独立点集就是在一个图中选一些点，使得他们两两间没有路径相连。
性质：最大独立点集=|V|-最小顶点覆盖=|V|-最大匹配数
证明：
这个搞清楚最小顶点覆盖之后就很好证明了。
因为最小顶点覆盖是选择最少的一些点，使它们覆盖所有的边。那我们把这些选出来的点删去之后，图中就不存在边了，剩下的点就是最大独立点集了。
比如还是这个图
它的最小点覆盖集是左边那俩点，我们把左边这两个点删掉，图中就没有边了，右边这三个点就是独立的了。
好多东西啊，先不写了，碰到题再说。