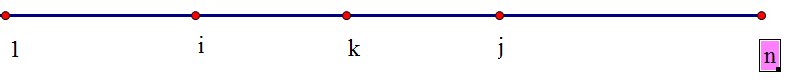目录
概述
首先说明一点,这种方法不是什么题都可以用的,我们要判断DP的情况,看是否能够使用平行四边形不等式来进行优化。一般来说,这种优化还是可以很容易看出来的。
首先两个满足的性质。
四边形不等式
如果有
那么这一个w数组(其实可以说成是函数)满足四边形不等式。看起来比较难理解,四边形不等式是什么东西。我们结合一个图来看,其实这个东西并不难
在图片中,可以明显地看出(i,j)与(i',j')小于对角线的长度,当然,图形如果不一样的话是可以等于的,这就是比较好理解的四边形不等式。
决策单调性
如果有,那么可以知道w是具有单调性的。
当然,上述的判断是比较麻烦的,判断起来十分不方便,于是,我们便可以用朴素的DP算法来打表判断。
其实还有一种方法,那就是看最优决策。
最优决策
这里先列一个状态转移方程,要不然不好说。
设s[i][j]为dp[i][j]的k值最优值,即当k取s[i][j]时,我们dp[i][j]的值最小。
那么问题来了,这东西该如何判断呢。
那么我们就需要根据题目,尝试比较s[i][j-1],s[i][j],s[i+1][j]等数的大小关系。这样我们就可以确定k的范围。几乎做到了降维的作用,这对于时间的优化可以说是非常大的。
例题
Post Office
题目描述
There is a straight highway with villages alongside the highway. The highway is represented as an integer axis, and the position of each village is identified with a single integer coordinate. There are no two villages in the same position. The distance between two positions is the absolute value of the difference of their integer coordinates.
Post offices will be built in some, but not necessarily all of the villages. A village and the post office in it have the same position. For building the post offices, their positions should be chosen so that the total sum of all distances between each village and its nearest post office is minimum.
You are to write a program which, given the positions of the villages and the number of post offices, computes the least possible sum of all distances between each village and its nearest post office.
有一条笔直的公路,公路旁边有村庄。高速公路用一个整数轴表示,每个村庄的位置用一个整数坐标标识。没有两个村庄处于相同的位置。两个位置之间的距离是它们的整数坐标的差的绝对值。
一些村庄会建邮局,但不一定所有的村庄都会建。一个村庄和它的邮局有相同的位置。在兴建邮政局时,应选择邮政局的位置,使每个村与其最近的邮政局之间的距离总和最少。
您需要编写一个程序,根据村庄的位置和邮局的数量,计算每个村庄与其最近的邮局之间的所有距离的最小可能和。
输入
第一行包含两个整数:第一行是村庄数V, 1 <= V <= 300,第二行是邮局数P, 1 <= P <= 30, P <= V。这些V整数是村庄的位置。对于每个位置X,它保持1 <= X <= 10000。
输出
第一行包含一个整数S,它是每个村庄与其最近邮局之间所有距离的总和。
样例输入
10 5
1 2 3 6 7 9 11 22 44 50样例输出
9解题思路
DP思路很好想吧。用dp[i][j]来表示前i个村庄有j个邮局。
。
我们看一看状态转移方程。到i时有j个村庄。到k时有j-1个村庄,那么k就是一个分界点,w我们暂时用来表示花费,其实我们可以知道,从k + 1 到 i中间的这一些村庄是肯定有两种情况的,有些还是要去第j-1个邮局,而有些就要去到第j个邮局,那么我们便要找到这一个分界点,使状态最优了。
其实根据我们数学的常识,找分界点并不难,若要花费最小,我们最好要保持两边的均衡,于是,取中间的那个村庄(中位数)即可。在这里,估计会有人质疑。我们其实也可以用反证的思想去证明,若中位数不优,那么往左或往右移一定会更小,这个区间两边的村庄个数最多只相差1(两个中位数情况任选其一),我们往左右移是一定不可能最小的。那么分界点弄出来了。但我们还要求这些村庄的距离和。
这里我们就需要用新的方法进行优化
我们需要进行预处理,用sum1[i]来表示从1到i的所有村庄到第一个村庄的距离总和,用sum2[i]来表示从i到n的所有村庄到最后一个村庄的距离总和。但这两个数组有什么用呢。其实,有了这两个数组我们就可以求出w了。
就是这样求的,看起来很复杂的样子。
我们结合图来看吧。
sum1[j] - sum1[k]就是求出了k到j这一段的村庄到1的距离。然而,我们求他们到1的距离是没有啥用的,因此,我们就需要减去k到j这一段村庄中多走的1到k这一段路程。如下图

同样,sum2也是一样的操作,这个时候,可能有人会尝试一下,可否反着来,即
乍一看好像没有问题。。。。实际上是有的,其实放在实际操作中还比较明显。我们由前面的推导可以知道,我们需要求k到j这一部分村庄到k的距离与i到k这一部分村庄到k的距离,如果像这样,不就变成了求k到j这一部分村庄到j的距离加上i到k这一部分村庄到i的距离吗?
的确,如果反着来,就是这样的操作。
w求完了,接下来就是做DP了,不过,DP有三个变量,至少也是三重循环,这道题虽然能过,但我们还是想着再优化一下,的确,这道题就需要用平行四边形优化。
我不管这么多性质,直接看最优决策点之间的关系,用s[i][j]表示令dp[i][j]最优的k。
那么如果j+1,就是说要多修一个邮局,你那么相应的决策点一定会往后移,你想吧,一段的点,本来平均分配,然而现在多了一个点,肯定给它空间,那么决策点必然后移,
所以s[i][j] <= s[i][j + 1]
要让我们的判断的s可以运用到程序中,j我们就不再管了,再来看i,如果i - 1,那么意味着少了一个村庄,那么,原来的决策点可能不平衡了。那么相应地要往多的那边移以此保持平衡态,减少村庄的那边,它是肯定不会移的。
那么s[i - 1][j] <= s[i][j]。
所以s[i - 1][j] <= s[i][j] <= s[i][j + 1]
我们dp的k的范围其实就出来了那么便可以快速地做了
#include<cstdio>
#include<cmath>
#include<cstring>
#include<iostream>
#include<vector>
#include<queue>
#include<map>
#include<cstdlib>
#include<algorithm>
#define N 1005
using namespace std;
int n,p,a[N],dp[305][305] , w[305][305] , sum1[305] , sum2[305] , s[305][305];
int main(){
memset(dp,0x3f,sizeof(dp));
scanf("%d%d",&n,&p);
for (int i = 1 ;i <= n; i ++ ){
scanf("%d",&a[i]);
}
for (int i = 1; i <= n;i ++ ){//求出1到i每个村庄到1的距离
sum1[i] = sum1[i - 1] + a[i] - a[1];
}
for (int i = n ;i >= 1 ;i -- ){//求出n到i每个村庄到n的距离
sum2[i] = sum2[i + 1] + a[n] - a[i];
}
for (int i = 1;i <= n;i ++ ){//预处理出i,j中建一个邮局所需要的花费
for (int j = i + 1;j <= n ; j ++ ){
if (i == j)
w[i][j] = 0;
else{
int t = (i + j)/2;
w[i][j] = sum1[j] - sum1[t] - (j - t) * (a[t] - a[1]) + sum2[i] - sum2[t] - (t - i) * (a[n] - a[t]);
}
}
}
dp[0][0] = dp[1][1] = 0;
for (int i = 1 ;i <= n ;i ++){
for (int j = min(i,p) ;j >= 1; j --){
if (s[i][j + 1] == 0)//如果没有值,我们赋一个边界值
s[i][j + 1] = i - 1;
if (s[i - 1][j] == 0)
s[i - 1][j] = min(i - 1 ,j - 1);
if (i == j){
dp[i][j] = 0;
continue;
}
for (int k = s[i - 1 ][j] ; k <= s[i][j + 1] ;k ++ ){//枚举k值
if (dp[i][j] > dp[k][j - 1] + w[k + 1][i]){
dp[i][j] = dp[k][j - 1] + w[k + 1][i];
s[i][j] = k;//更新最优决策点
}
}
}
}
printf("%d",dp[n][p]);
}
总结
总的来说,这道题并不是十分轻松或者说是困难,平行四边形的优化在这道题倒不是特别重要,因为数据量小,不优化依旧可以过。但利用前缀和与后缀和求出w数组这也许才是这道题的关键部分,这里还是比较难的,但理解起来却是不难。可以说练这一道题还是有一定的意义。
Monkey Party
题目链接
就是环形的合并石子,我们将原数组复制一份到后面还是跟普通DP一样做。
解题思路
首先,列状态转移方程。我们这样看,如果从i,j这一段要合并,最后的花费就一定是i,j的石子个数,先前的花费就要看有哪一个k使得(i,k)(k+1,j)这两组合并最小了。而求(i,k)则。。。是不是很像递归,其实不然,这就是状态转移方程。
其中cost很容易求出来,就是两个前缀和相减,sum[j] - sum[i - 1].由于题目说是环形,我们复制数组,再做DP即可。
此题枚举顺序是一个关键。k是比i大的,我们需要倒着枚举i,k又比j小,我们就要顺着枚举j,k顺着枚举即可。
最后,以每一个点为开头看看它们dp最小值。即ans = min{dp[i][i + n - 1]}。
不过,这道题依旧可以用四边形不等式来进行优化。还是那种思路。如果j+1,那么原本i,j的最优决策点s[i][j]是一定会小于等于s[i][j + 1],同样的,s[i - 1][j] <= s[i][j]。
不过这道题的枚举顺序不同,我们就不能用这种方式来优化,改一下。用s[i][j - 1] <= s[i][j] <= s[i + 1 ][j]即可。
#include<cstdio>
#include<cmath>
#include<cstring>
#include<iostream>
#include<vector>
#include<queue>
#include<map>
#include<cstdlib>
#include<algorithm>
#define N 1005
using namespace std;
int n,a[N * 2] , sum[N * 2] , dp[N * 2][N * 2] ,s[N * 2][N * 2] ;
long long ans = 1e15;
int main(){
while (scanf("%d",&n)!=EOF){
ans = 1e15;
memset(dp,0x3f,sizeof(dp));
memset(sum,0,sizeof(sum));
memset(s,0,sizeof(s));
for (int i = 1 ;i <= n ;i ++){
scanf ("%d",&a[i]);
a[i + n] = a[i];
}
for (int i = 1;i <= n * 2;i ++){
sum[i] = sum[i - 1] + a[i];
s[i][i] = i;
}
for (int i = 0;i <= 2 * n;i ++)
dp[i][i] = 0;
for (int i = n * 2;i >= 1 ;i -- ){
for (int j = i + 1;j <= n * 2 ;j ++ ){
if (!s[i][j - 1])
s[i][j - 1] = i;
if (!s[i + 1][j])
s[i + 1][j] = j - 1;
if (i == j)
continue;
for (int k = s[i][j - 1] ;k <= s[i + 1][j] ;k ++ ){
if (dp[i][j] > dp[i][k] + dp[k + 1][j] + sum[j] - sum[i - 1]){
dp[i][j] = dp[i][k] + dp[k + 1][j] + sum[j] - sum[i - 1] ;
s[i][j] = k;
}
}
}
}
for (int i = 1 ;i <= n; i ++){
ans = ans < dp[i][i + n - 1]?ans:dp[i][i + n - 1];
}
printf("%lld
",ans);
}
}总结
这道题很坑。。。。主要我没仔细读题,他那个描述是英文的,我翻译大概看了一遍就没管了,上课讲了题目的,我以为理解了题目,最后发现这道题多组数据,害我错了很多次,这道题dp式子可以说是很单纯的,很少有两个都表示编号。环的处理方法不止这一种,据说还有一种方式叫破环为链,一次逛本校大佬ljh的博客看到过,在这里给一个链接。不是这道题的。感觉方式方法差不多。。。
评述
平行四边形优化我认为还是比较基础的DP优化,因为他的性质并不难找。仅仅需要假设然后想象一番就可以确定题目是否可以用平行四边形的优化了,计算量看来是不大的,也许是我现在接触到的题目比较基础的样子。但这一种处理的方式是比较巧妙的,因为平时做DP,哪里想到利用其中变量的关系来进行优化呢?因此,这一种优化方法我认为是需要熟记与运用的。