数据结构
数据结构其实就是一种存储数据的格式。可以有效的改善代码中数据的存储。
稀疏矩阵
对于一个二维数组,如果数组中大部分元素为0,那么会造成内存空间极大的浪费。因此,设计一种针对稀疏数组的数据结构就很有必要,例如:

可以看出,稀疏矩阵是将一种矩阵转换,将N行M列的矩阵转换为X行3列的矩阵,当矩阵为稀疏矩阵时,这种存储数据的结构更能符合压缩的功能。
二维数组转换为稀疏矩阵
步骤1:保存稀疏矩阵的第一行,N、M、count(遍历二维数组得到非0元素个数)
步骤2:遍历数组,保存非0数组的行数、列数、以及元素的值。
稀疏矩阵转换为二维数组
步骤1:从第一行获得二维数组的行、列。
步骤2:遍历稀疏矩阵,将二维数组中对应位置填值。
队列
队列是一种先进先出的数据结构,队列在计算机系统中有很重要的作用,比如在缓存机制中,就是将磁盘的值按照队列形式排列,先存进来的优先被cpu使用。
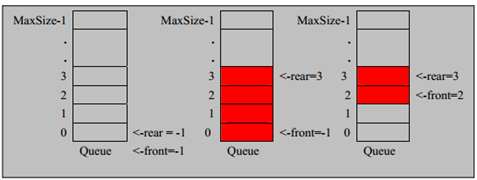
(一种顺序队列)
队列的元素:长度、队头、队尾。
顺序队列
顺序队列在物理中的存储方式是连续的,可以保存在数组中。
初始化:队列需要使用一个队头和队尾的指示标志(指针/索引),队头和队尾一开始一定是相等的(队头队尾相等是空队的判断条件)。
判空:队头=队尾
判满:在非循环队列中,队满的标志仅是:队尾==MaxSize-1(指向最后一个元素);在循环队列中,队满的标志是:(队尾+1) mod MaxSize==队头(即在循环上,队尾比队头多一个元素)
入队:首先,判断队列是否已满,满了就无法入队,若没有满,则将元素赋值给队尾,并使队尾指向下一个索引(这里的下一个是相对循环而言,若下一个索引大于MaxSize-1,则需指向第一个元素),需取模:
rear=(rear+1)%MaxSize
出队:首先,判断队列是否为空,若是空队就无法取出元素,若非空队,则从队头取元素,即,将队头指向的元素取出并返回,然后使队头的元素指向下一个索引。(同样的,下一个需要判断其索引是否大于长度),需取模。
front=(front+1) % MaxSize
显示队列里的值:用这种方法得到的队列,其数组并不是真的入队出队,数据虽然被覆盖,但并没有删除,因此,出队操作并没有出数组。因此,显示的时候需要判断,队头和队尾,然后将有效的数据显示出来。这里就有一个有效数据的概念,这里的有效数据是:
(rear-front +MaxSize) % MaxSize
因此,遍历的起点是队头,队尾是队头+有效数据。而索引值则需要取模处理,因为可能超过长度。
单链表
链表是树和图的基础,也是区别于顺序存储的另一种存储方式。在jvm中,如果一个对象不被引用,则会被垃圾回收,这里就用到了链表的实现。

最简单的链表就是单链表,单链表的增删改查是很简单的。这里不多介绍。主要举几个面试的例子。
1.单链表中有效节点的个数
很简单,遍历链表,当当前节点的next域不为空时,就计数。
2.查找单链表中倒数第k个节点
方案1:先得到链表的长度,然后根据计算查找第(长度-k)个节点,即可得到该节点。
方案2:使用两个辅助指针,第一个指向第k个节点,第二个指向第1个节点,然后两个指针同时向后移动,当指向第一个的节点移到最后,则第二个指针指向的就是倒数第k个。
3.单链表的翻转
使用头插法,新建一个链表,每次遍历得到节点就插到新链表的头部,这样先插的会到后面去,实现了链表的翻转。
4.从尾到头打印单链表
使用一个辅助栈,先将遍历得到的节点值依次压栈,然后遍历结束之后,依次出栈。
5.合并两个有序的单链表,合并后仍然有序
定义一个新节点,然后定义两个游标指向两个链表的头结点,比较大小,如果小就将该节点插入新节点的后面,循环进行,直到其中一个链表被遍历完,然后将剩下的链表插入到新节点的后面。
双向链表
设计链表的时候,有前指针域和后指针域。双向链表不需要翻转。
删除
对于单链表而言,要想删除当前节点,不能直接遍历到当前的节点,而是需要遍历到当前节点的前一个,然后将其next域赋值给当前节点的next域。
双向链表不需要这么做,遍历到当前节点,将当前节点的next域赋值给当前节点的pre域,将后面节点的pre域赋值给当前节点的next域。然后删除即可。
单向环链表
该链表只比单链表增加了一条链表末尾指向链表开头的指针。
解决约瑟夫环问题

稍加分析就可以知道,设置两个指针,first和help,初始化时,first指向k,help指向k-1,表示的是first和help一个在头,一个在尾,然后后移m个,将help指向first后一个节点,形成环路,然后删除first指向的节点,将first+1,依次循环直到环为空。
栈
栈是一种先进后出的数据结构,在计算机操作系统里面有很广泛的应用。
使用栈来完成一个计算器。
1.中缀表达式
中缀表达式就是计算表达式的原始表达式,例如
2*(3+2)-6/3
直接利用中缀表达式,配合栈的使用,可以得到计算结果。

这里主要是扫描到符号的时候,需要判断符号的优先级。如果栈中的优先级大于当前的,就需要先计算,然后再压栈。其实这里的算法是有问题的
3+4-8/2+5*5/5-8+9
像上面的计算式,如果采用上面的流程,会导致最后7-4+5-8+9出现,计算从后往前,会破坏四则运算从左往右的计算规则:结果为7,实际结果为9改进在3.2,代码如下:

public int cal(String str){ Stack<String> num=new Stack<String>(); Stack<String> oper=new Stack<String>(); int index=0; int sum=0; while(true){ //如果该字符是一个符号 if(isoper(str.charAt(index))){ if(oper.isEmpty()){ oper.push(str.substring(index,index+1)); }else { if(priority(str.charAt(index))<=priority(oper.peek().charAt(0))){ //先pop出来,然后计算 while(!num.isEmpty() && !oper.isEmpty() && priority(str.charAt(index))<=priority(oper.peek().charAt(0))) { int num1 = Integer.parseInt(num.pop()); int num2 = Integer.parseInt(num.pop()); char ope = oper.pop().charAt(0); int res = call(num1, num2, ope); num.push(("" + res)); } oper.push(str.substring(index, index + 1)); }else{ oper.push(str.substring(index,index+1)); } } }else{ num.push(str.substring(index,index+1)); } index++; if(index>=str.length()){ break; } }
2.后缀表达式
将中缀表达式转换为后缀表达式之后,就不需要判断优先级,直接进行运算,得到的就是结果
如何将中缀表达式转换为后缀表达式

如何用中缀表达式计算
![]()
递归
递归是函数自己调用自己,但事实上,它在调用过程中和普通调用没有区别。
递归调用的机制。
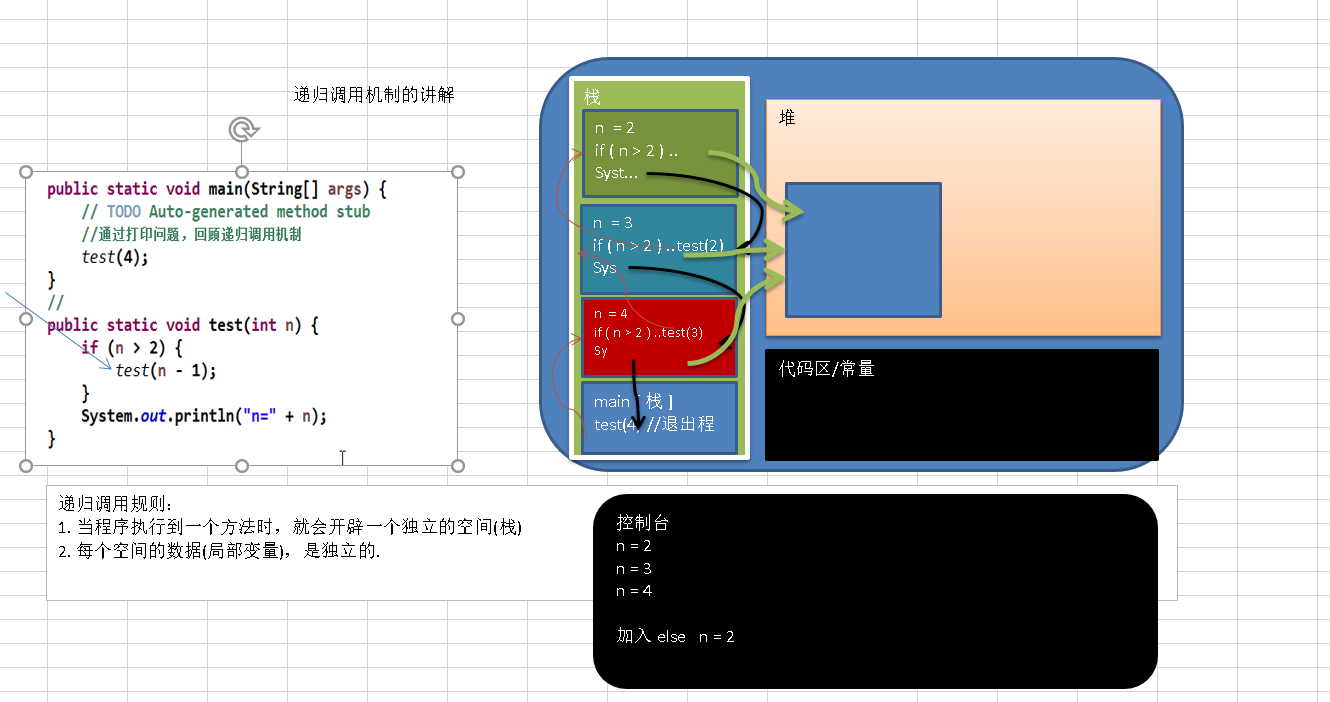
从上图可以看出,执行main方法后在栈空间开辟一个栈的数据结构,mian方法在栈底,调用test方法,一旦方法进行了调用,就会在栈空间入栈,test方法里有调用,仍然会入栈,。。。直到,不满足调用条件,会执行调用之后的打印代码,然后当调用函数执行完,就会自动出栈操作,释放空间。然后返回上一层的打印代码,。。。。直到main函数执行结束。
递归执行的规则

回溯
在迷宫问题上,如何从入口找到出口。可以使用回溯,回溯问题可以使用递归来解决,即设置多个递归入口,设置迷宫的寻找策略。

分析:从入口开始,尝试从上下左右四个方向去寻找出口,如果四个方向都尝试了以后还没有找到出口,说明这个路是不通的,需要往回走,这就是回溯。
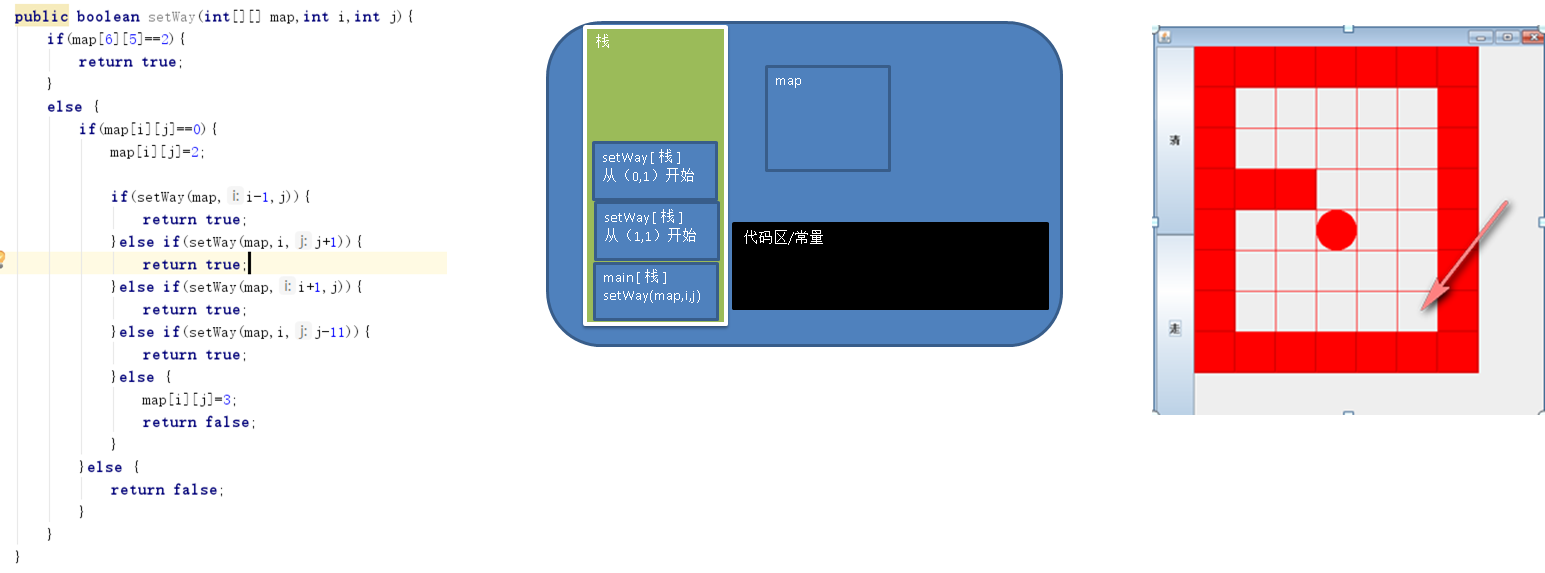
代码如下,可以分析其递归调用的过程。
main方法入栈,
调用setWay方法,入栈,map为引用类型,不会在调用中终止寿命,因此会发生改变。但基础类型会发生改变。此时是从(1,1)开始,将其设置为2,然后调用setWay(map,0,1)。
调用后直接返回false,回溯到栈(1,1),
调用setWay(map,1,2),可以进入,将其设置为2,然后直接调用setWay(map,0,2),直接返回false,回溯到栈(1,1)。。。。
。。。
八皇后问题,通过回溯递归来解决

限制:每一行必有且只有一个皇后。
需要确定的摆放位置:第一行的皇后放在第几列,第二行的皇后放在第几列。。。。。可以使用一个数组:int[] array = new int[8];,下标代表的行,值代表的列。
private void check(int n) { if(n == max) { //n = 8 , 其实8个皇后就既然放好 print(); return; } //依次放入皇后,并判断是否冲突 for(int i = 0; i < max; i++) { //先把当前这个皇后 n , 放到该行的第1列 array[n] = i; //判断当放置第n个皇后到i列时,是否冲突 if(judge(n)) { // 不冲突 //接着放n+1个皇后,即开始递归 check(n+1); // } //如果冲突,就继续执行 array[n] = i; 即将第n个皇后,放置在本行得 后移的一个位置 } }
对于以上递归代码,每次循环都会有八个递归入口,判断是否进入的依据是该入口是否满足八皇后的要求。
冒泡排序
冒泡排序的精髓在于每一次循环都会把数组的最后一个值确定下来,或是最大,或是最小。

从以上的例子就可以看出。每次循环都能找到比较里面最大的,然后把它交换到最后,下一次循环就不会比较这个值。时间复杂度为T(n^2)

package com.liuixnghang.test; import org.junit.Test; public class Maopao { @Test public void run(){ int [] a=new int[]{2,1,3,5,4}; maopao(a); } public void print(int[] a){ for (int i : a) { System.out.print(i +" "); } System.out.println(); } public void maopao(int[] a){ boolean falg=false; for(int i=0;i<a.length-1;i++){ for(int j=0;j<a.length-1-i;j++){ if(a[j]>a[j+1]){ int temp=a[j]; a[j]=a[j+1]; a[j+1]=temp; falg=true; } } if (falg==false){ break; }else{ falg=false; } print(a); } } }
选择排序
选择排序重在选择,为了避免一直交换,可以设置一个min值,每次都遍历一遍数组,得到最小值,将其与数组第一个值交换,这样,循环长度-1次后,就得到了排序。

可以知道这样避免了一直去交换
代码如下:

package com.liuixnghang.test; import org.junit.Test; public class Choose { @Test public void run(){ int [] a=new int[]{101,34,199,1,-1,90,123}; choose(a); } public void choose(int[] a){ for(int i=1;i<a.length;i++){ int minIndex=i-1; int min=a[minIndex]; //每次循环都会选择最小的数出来放在第一个地方 for(int j=i;j<a.length;j++){ if(a[j]<min){ min=a[j]; minIndex=j; } } if(minIndex!=(i-1)){ a[minIndex]=a[i-1]; a[i-1]=min; } print(a); } } public void print(int[] a){ for (int i : a) { System.out.print(i +" "); } System.out.println(); } }
插入排序
其主要思想是,将一部分先排好序,每次从后面的一个往有序的里面插,形成新的有序序列,直到所有都有序。
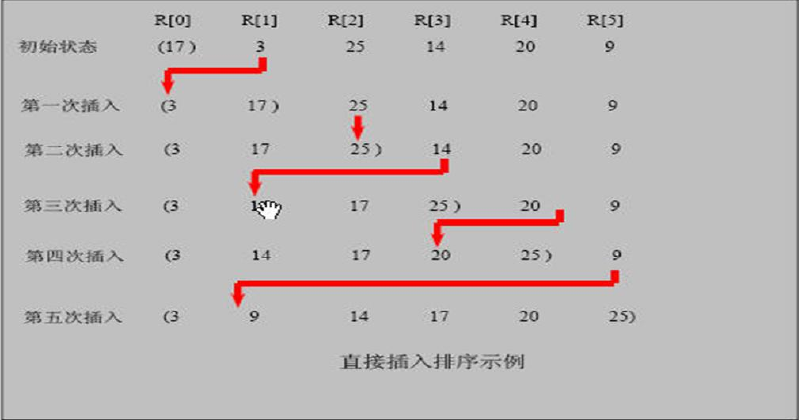
插入过程是先从有序的最后一个开始找自己的插入位置。
代码如下:

package com.liuixnghang.test; import org.junit.Test; public class Insert { @Test public void run(){ int [] a=new int[]{4,7,2,32090,-1218,-9,238,1219,-11,2}; insert(a); } public void print(int[] a){ for (int i : a) { System.out.print(i +" "); } System.out.println(); } public void insert(int[] a){ for(int i=1;i<a.length;i++){ //待插入的值 int insertValue=a[i]; //插入位置 int insertIndex=i-1; //从第i-1个位置开始寻找插入位置,没找到需要将数组向后移 while(insertIndex>=0 && insertValue<a[insertIndex]){ a[insertIndex+1]=a[insertIndex]; insertIndex--; } a[insertIndex+1]=insertValue; print(a); } } }
希尔排序
是插入排序的升级版,在插入排序中,如果较小的元素在最后面,那么插入效率很变得很慢,为了解决这个问题,可以把数据隔着步长分组,对每组的数据进行插入排序,这样就可以快速的使小的数据移动到前面来。
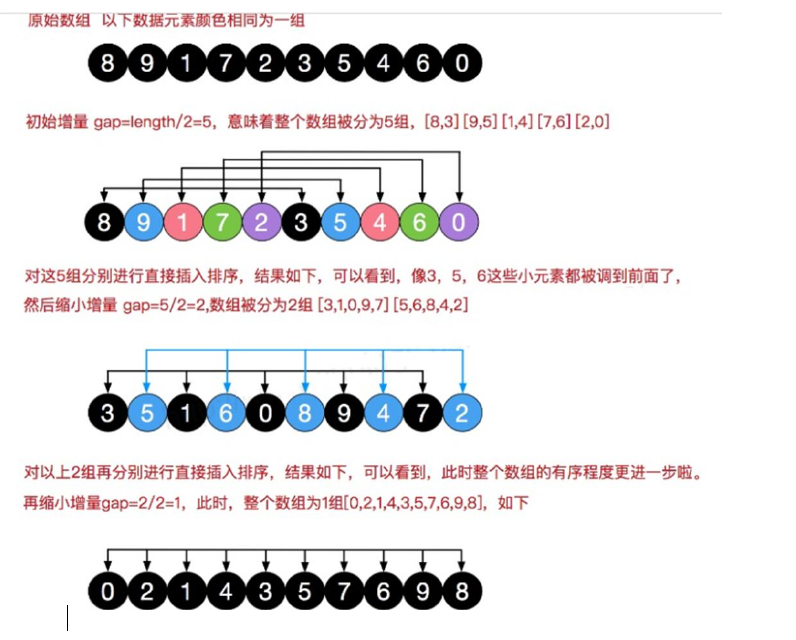
在刚开始分为5组,插入排序的对象是两个数据,然后变成五个,最后变为10个。步长在不断的改变当中。
使用交换法实现。不是使用移动来插入,而是每次都插入实现插入。

package com.liuixnghang.test; import org.junit.Test; public class Shell { @Test public void run(){ int [] a=new int[]{8,9,1,7,2,3,5,4,6,0}; shell(a); } public void print(int[] a){ for (int i : a) { System.out.print(i +" "); } System.out.println(); } public void shell(int[] a){ for(int gap=a.length/2;gap>0;gap/=2) { for (int i = gap; i < a.length; i++) { for (int j = i - gap; j >= 0; j -= gap) { if (a[j] > a[j + gap]) { int temp = a[j]; a[j] = a[j + gap]; a[j + gap] = temp; print(a); } System.out.println("----"); } System.out.println("----"); } System.out.println("----"); } } }
使用移动法插入,就是对每次分组采用插入排序。

package com.liuixnghang.test; import org.junit.Test; public class Shell { @Test public void run(){ int [] a=new int[]{8,9,1,7,2,3,5,4,6,0}; shell2(a); } public void print(int[] a){ for (int i : a) { System.out.print(i +" "); } System.out.println(); } public void shell(int[] a){ for(int gap=a.length/2;gap>0;gap/=2) { for (int i = gap; i < a.length; i++) { for (int j = i - gap; j >= 0; j -= gap) { if (a[j] > a[j + gap]) { int temp = a[j]; a[j] = a[j + gap]; a[j + gap] = temp; print(a); } } print(a); } } } public void shell2(int[] a){ //使用移动法 for(int gap=a.length/2;gap>0;gap/=2){ for(int i=gap;i<a.length;i++){ //保存待移动的数 int temp=a[i]; int j=i-gap; while(j>=0 && temp<a[j]){ a[j+gap]=a[j]; j-=gap; } a[j+gap]=temp; print(a); } } } }
快速排序
快速排序是冒泡排序改进而来,通过空间换时间,有效的降低了时间复杂度,冒泡排序每次固定一个最大值排在后面,快速排序每次固定一个基准数放在其位置上。
快速排序也有两种实现方式,主要区别在于如何移动数据,使得基准数据排在准确位置。
1.挖坑法:
设置两个指针left和right指向数组的头和尾,选取基准数,可随机选择。但需要将该基准数移动第一位。
记住选取基准位置的index,此索引就是坑。
从尾部right开始,向前寻找比基准数小的数,找不到就一直向前移,直到找到这样的数(前提是right要比left大)
将找到的这个数填入坑中,此时,right指向的数成为了新的坑
然后left从头部开始,向后寻找比基准大的数,找不到就一直向后,直到找到,(前提是right要比left大)
找到这个数,继续填坑,此时left指向的数成为了新坑。
直到right和left重合。这一轮就结束了,
把基准的数填在重合的索引里,然后
然后进行递归,在right左边,继续进行这样的操作。
代码如下:

package com.liuixnghang.test; import org.junit.Test; public class Waken { @Test public void run(){ int [] a=new int[]{8,9,1,7,2,3,5,4,6,0}; waken(a,0,a.length-1); } public void print(int[] a){ for (int i : a) { System.out.print(i +" "); } System.out.println(); } public void waken(int a[],int left,int right){ //设置索引 int l=left; int r=right; //设置基准 int juzhun=a[left]; //循环填坑 if(l<r) { while (l != r) { //从尾部开始,找比基准小的元素 while (l < r && a[r] >= juzhun) { r--; } //找到了这样的数,将值填到坑中 if (l < r) { a[l] = a[r]; l++; } //从尾部开始,找比基准小的元素 while (l < r && a[l] <= juzhun) { l++; } //找到了这样的数,将值填到坑中 if (l < r) { a[r] = a[l]; r--; } } a[l] = juzhun; print(a); waken(a, left, r - 1); waken(a, l + 1, right); } } }
2.指针交换法
设置两个指针left和right指向数组的头和尾,选取基准数,可随机选择。但需要将该基准数移动第一位。
从left指针和right指针开始,向中间靠拢,如果left遇到比基准大的指针,需要停下来,right遇到比基准小的指针,也需要停下来。
两个指针指向的数交换。然后继续交换,直到两个指针重合。然后将第一位中基准元素与重合位元素交换,此轮结束。
代码如下:

package com.liuixnghang.test; import org.junit.Test; public class Jiaohuan { @Test public void run(){ int [] a=new int[]{8,9,1,7,2,3,5,4,6,0}; jiaohuan(a,0,a.length-1); } public void print(int[] a){ for (int i : a) { System.out.print(i +" "); } System.out.println(); } public void jiaohuan(int[] a, int left, int right){ //设置索引 int l=left; int r=right; //设置基准 int juzhun=a[left]; while(l!=r){ //寻找left指向比基准小的数 while(l<r &&a[r]>juzhun){ r--; } //寻找left指向比基准大的数 while(l<r &&a[l]<=juzhun){ l++; } if(l<r){ int temp=a[l]; a[l]=a[r]; a[r]=temp; } } //需要退指针 //将基准数和相等时的位置交换 int temp=a[l]; a[l]=a[left]; a[left]=temp; print(a); jiaohuan(a,left,r-1); jiaohuan(a,l+1,right); } }
(需要注意的一点是,需要先移动r指针,才会在重合的位置是所需要的)
归并排序
归并排序使用了分治的思想,先利用递归,将数组分为单个的数,然后在递归出栈的时候,就可以每两个进行排序,然后到下一个栈,每四个进行排序,到最后合并为一个有序数组
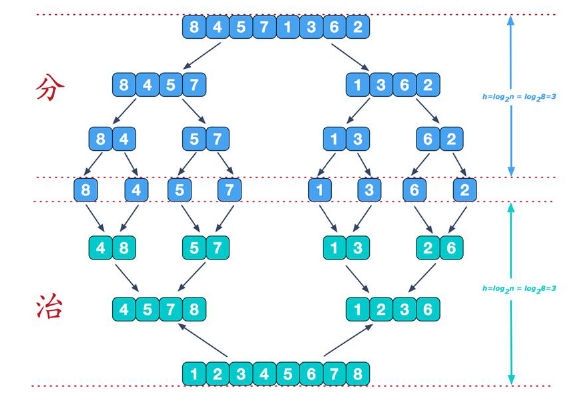
归并排序说明:其递归可以这样设计:第一次分为一半,然后分为四分之一。。。。直到分为1,无法再分。
按照递归的栈原理,需要返回,在返回之前,将之前分开的按左右合并,合并规则就是小的在前,大的在后。
每次返回之前都合并,到返回mian函数的时候已经合并为一个有序的数组了。
代码如下:

package com.liuixnghang.test; import org.junit.Test; public class GuiBing { @Test public void run(){ int [] a=new int[]{8,9,1,7,2,3,5,4,6,0}; int [] temp=new int[a.length]; guibing(a,0,a.length-1,temp); print(a); } public void print(int[] a){ for (int i : a) { System.out.print(i +" "); } System.out.println(); } public void guibing(int [] a,int left,int right,int[] temp){ if(left<right){ int mid=(left+right)/2; //向左递归进行分解 guibing(a,left,mid,temp); guibing(a,mid+1,right,temp); hebing(a,left,mid,right,temp); } } public void hebing(int[] a,int left,int mid,int right,int[] temp){ //将左边和右边排序 int i=left;//左边数组的起始索引 int j=mid+1;//右边数组的起始索引 int t=0;//t数组的起始索引 while(i<=mid && j<=right){ if(a[i]<=a[j]){ temp[t]=a[i]; t++; i++; }else{ temp[t]=a[j]; t++; j++; } } while(i<=mid){ temp[t]=a[i]; t++; i++; } while(j<=right){ temp[t]=a[j]; t++; j++; } //将temp中的数组拷贝在a中 t=0; int tempLeft=left; while(tempLeft<=right){ a[tempLeft]=temp[t]; t++; tempLeft++; } } }
基数排序
经典的用空间换时间的排序方式,排序需要10个数组,每个数组的长度与待排序数组长度一样多,很耗费空间。

以上就是基数排序的过程:
设置10个数组,逻辑上代表位数的个数位。
在第一轮排序中,按照数组中每个数的个位,将数依次填入每个桶中;
然后根据存的桶再依次拿出存入数组中,依次往复,
即可得到排序后的数组。
代码如下:

package com.liuixnghang.test; import org.junit.Test; import java.text.SimpleDateFormat; import java.util.Date; public class Jishu { @Test public void run(){ //测试快排的执行速度 // 创建要给80000个的随机的数组 int[] arr = new int[8000000]; for (int i = 0; i < 8000000; i++) { arr[i] = (int) (Math.random() * 8000000); // 生成一个[0, 8000000) 数 } System.out.println("排序前"); Date data1 = new Date(); SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss"); String date1Str = simpleDateFormat.format(data1); System.out.println("排序前的时间是=" + date1Str); jishu(arr); Date data2 = new Date(); String date2Str = simpleDateFormat.format(data2); System.out.println("排序前的时间是=" + date2Str); } public void print(int[] a){ for (int i : a) { System.out.print(i +" "); } System.out.println(); } public void jishu(int [] a){ //设置1个二维数组来存储10个一维数组 int [][] bucket=new int[10][a.length]; //设置一个数组来记录每个桶中的数据有几个 int bucketElementCounts[]=new int[10]; //这里需要得到数据中数的最大位数 int max=0; for(int i=0;i<a.length;i++){ if(a[i]>max){ max=a[i]; } } int maxLength=(max+"").length(); //进行循环 for(int i=0,n=1;i<maxLength;i++,n*=10){//对每一位进行处理 //把数据取出来放到对应的桶里 for(int j=0;j<a.length;j++){ //得到当前数据的位数 int digit=a[j] /n %10; //放到对应的桶中 bucket[digit][bucketElementCounts[digit]]=a[j]; bucketElementCounts[digit]++; } int index=0; //按桶的顺序,取出数,放到数组中 for(int k=0;k<bucketElementCounts.length;k++){ if(bucketElementCounts[k]!=0){ for(int l=0;l<bucketElementCounts[k];l++){ a[index++]=bucket[k][l]; } } //将bucketElementCounts中的数清零 bucketElementCounts[k]=0; } } } }
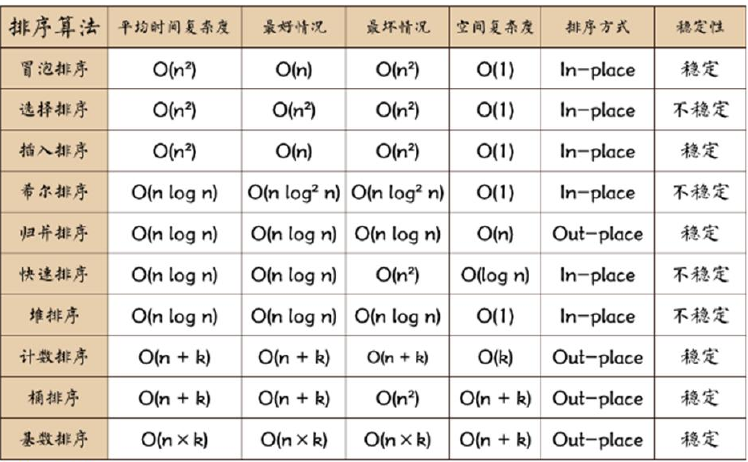
排序总结