树与二叉树

一.树的定义与基本术语

1.树的基本概念

树是n(n>=0)个节点的有限集合T。当n=0时，称为空树；当n>0时，该集合满足如下条件：

(1)其中必有一个称为根（root)的特定结点，它没有直接前驱，但有零个或多个直接后继。

(2)其余n-1个结点可以划分成m(m>=0)个互不相交的有限集T₁,T₂,...,T_m,其中T_i又是一棵树，称为树的子树。每棵子树的根节点有且只有一个直接前驱，但有零个或多个直接后继。

如下图，给出了一棵树的逻辑结构图示，如同一颗倒长的树：

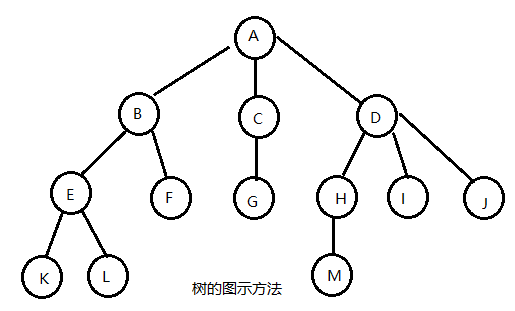
2.树的图解表示方法

(1)倒置树结构（树形表示法),如上图所示。

(2)除了树形表示法，还有文氏图表示法（嵌套集合表示法）、广义表形式（嵌套括号表示法）、凹入表示法等，在这不做详解，具体可以参考《数据结构-----有C语言描述》。

3.树的相关术语

(1)结点：包括一个数据元素及若干指向其他结点的分支信息

(2)结点的度：一个节点的子树的个数称为该结点的度

(3)叶节点：度为0的结点，即无后继的结点，也称终端结点

(4)分支结点：度不为0的结点，也称非终端结点

(5)结点的层次：从根节点开始定义，根节点的层次为1，根的后继的结点的层次为2，依次类推

(6)树的度：树中所有结点度的最大值

(7)树的高度（深度）：树中所有结点的层次的最大值

(8)森林：将一个非空树的根节点删除后，树就变成一个森林，反之给森林加一个统一的根节点后，森林就变成一棵树

(9)同构：对两棵树，结点对应相等，对应结点的相关关系也相等

(10)孩子结点：一个节点的直接后继

(11)父亲结点：一个节点的直接前驱

(12)兄弟结点：同一双亲结点的孩子结点之间互称兄弟结点

例如，具有3个结点且不同构的有序树共有以下5种：

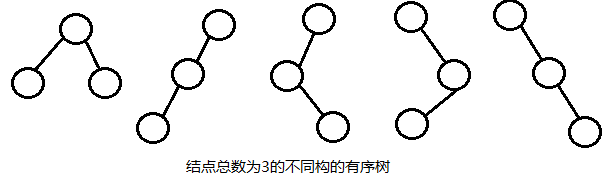
4.树的基本操作

InitTree:初始化树

DestoryTree:销毁树

CreatTree:创建树

TreeEmpty:判断树是否为空

Root:返回非空树的根

Delete:删除节点

二.二叉树

1.二叉树的定义与基本操作

定义：满足以下两个条件的树结构称为二叉树：（Binary Tree）

(1)每个结点的度都不大于2。

(2)每个结点的孩子结点次序不能任意颠倒

由此定义可以看出，一个二叉树中的每个节点只能包含有0、1或2个孩子，而且每个孩子有左右之分，位于左边的孩子称为左孩子，位于右边的孩子称为右孩子。

如下图是二叉树的5种基本形态：

基本操作：与树的基本操作类似

2.二叉树的性质

(1)在二叉树的第i层至多有2^i-1个结点（i>=1)。

(2)深度为k的二叉树至多有2^k-1个结点。

(3)对于任意一棵二叉树T，若终端结点的个数（叶子节点的个数）为n₀，而其度为2的结点数为n₂,则n₀=n₂+1。（根据分支数与结点的关系推出）。

　　满二叉树：深度为k的二叉树有2^k-1个结点的二叉树。

　　完全二叉树：完全二叉树的结点1·n编号的位置序号与满二叉树的编号相同，即一一对应。

(4)具有n个结点的完全二叉树的深度为log₂n+1。

(5)对于有n个结点的完全二叉树，如果按照从上往下和从左往右的顺序对二叉树中的所有结点从1开始编号，则对于序号为i的结点有：

　　a.i=1,则序号为i的结点是根节点，无双亲结点；如果i>1;则序号为i的结点的双亲结点的序号为i/2(向下取整)。

　　b.如2i>n,则编号为i的结点无左孩子与右孩子。如果2i<=n,则序号为i的结点的左孩子序号为2i,右孩子结点序号为2i+1。

3.二叉树的存储结构

二叉树的结构是非线性的，每个结点最多可有两个后继。二叉树的存储结构有两种：顺序存储结构和链式存储结构。

(1)顺序存储结构

　　分完全二叉树、单支树这两种情况讨论，如下图：

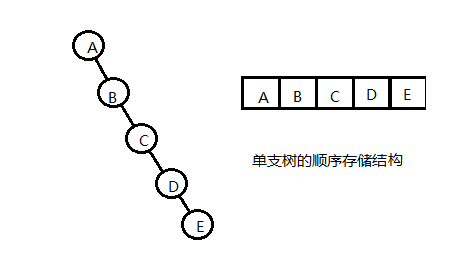
(2)链式存储结构

对任意的二叉树来说，每个结点只有一个双亲结点（根节点除外），最多有两个孩子。可以设计每个结点至少包括三个域：数据域、左孩子域和右孩子域，如下图所示：

用C语言定义的我二叉树的二叉链表结点结构如下：

1 typedef struct Node
2 {
3     DataType data;
4     struct Node * Lchild;
5     struct Node * Rchild;
6 }BiTreeNode,*pBiTree;

若一个二叉树含有n个结点，则它的二叉链表中必含2n个指针域，其中必有n+1个空指针域。（因为有n个结点，非空的链域必有n-1个，所以空的链域定有2n-（n-1）=n+1个）。

三.用C语言实现二叉树的基本操作

  1 //BTNode.c
  2 #include"BTree.h"
  3 
  4 BTNode * LeftChild(BTNode *pRoot)//获取左孩子
  5 {
  6     return pRoot != NULL ? pRoot->_pLift : NULL;
  7 }
  8 BTNode * RightChild(BTNode *pRoot)//获取右孩子
  9 {
 10     return pRoot != NULL ? pRoot->_pLift : NULL;
 11 }
 12 
 13 int HeightBTree(BTNode *pRoot)
 14 {
 15     int leftheight = 0;
 16     int  rightheight = 0;
 17     if (pRoot == NULL)
 18     {
 19         return 0;
 20     }
 21     leftheight = HeightBTree(pRoot->_pLift);
 22     rightheight = HeightBTree(pRoot->_pRight);
 23     return leftheight > rightheight ? leftheight+1 : rightheight+1;
 24 }
 25 
 26 int GetKLevelBTNodCount(BTNode *pRoot, int k)
 27 {
 28     if (pRoot == NULL||k<=0)
 29     {
 30         return 0;
 31     }
 32     if (1 == k)
 33         return 1;
 34     return GetKLevelBTNodCount(pRoot->_pLift, k-1) + GetKLevelBTNodCount(pRoot->_pRight, k-1);
 35 }
 36 
 37 int GetLeafBTnodCount(BTNode *pRoot)
 38 {
 39     if (pRoot == NULL)
 40     {
 41         return 0;
 42     }
 43     if (pRoot->_pLift == NULL&&pRoot->_pRight == NULL)
 44     {
 45         return 1;
 46     }
 47     return GetLeafBTnodCount(pRoot->_pLift) + GetLeafBTnodCount(pRoot->_pRight);
 48 }
 49 
 50 int GetBTNodeCount(BTNode *pRoot)
 51 {
 52     if (pRoot == NULL)
 53     {
 54         return 0;
 55     }
 56     return GetBTNodeCount(pRoot->_pLift) + GetBTNodeCount(pRoot->_pRight) + 1;
 57 }
 58 
 59 void DestoryBinTree(BTNode **pRoot)//销毁二叉树
 60 {
 61     assert(pRoot);
 62     if (*pRoot)
 63     {
 64         DestoryBinTree(&(*pRoot)->_pLift);//销毁左子树
 65         DestoryBinTree(&(*pRoot)->_pRight);//销毁右子树
 66         free(*pRoot);
 67         *pRoot = NULL;
 68     }
 69 }
 70 
 71 BTNode *CopyBinTree(BTNode *pRoot)//拷贝二叉树
 72 {
 73     BTNode *pNewNode = NULL;
 74     if (pRoot)
 75     {
 76         
 77         pNewNode = BuyNewNode(pRoot->data);
 78         //拷贝左子树
 79         if (pRoot->_pLift)
 80             pNewNode->_pLift = CopyBinTree(pRoot->_pLift);
 81         //拷贝右子树
 82         if (pRoot->_pRight)
 83             pNewNode->_pRight = CopyBinTree(pRoot->_pRight);
 84     }
 85     return pNewNode;
 86 }
 87 
 88 void CreatBinTree(BTNode **pRoot, char *str, int size, int *index,BDataType invalid)//创建二叉树
 89 {
 90     assert(pRoot != NULL);
 91     assert(index);
 92     if ('#'!=str[*index]&&(*index)<size)
 93     {
 94         *pRoot = BuyNewNode(str[*index]);
 95         (*index)++;
 96         CreatBinTree(&(*pRoot)->_pLift, str, size, index,invalid);//创建左子树
 97         (*index)++;
 98         CreatBinTree(&(*pRoot)->_pRight, str, size, index,invalid);//创建右子树
 99     }
100 }
101 BTNode *BuyNewNode(BDataType data)//购买新节点
102 {
103     BTNode * pNewNode = (BTNode *)malloc(sizeof(BTNode));
104     if (pNewNode == NULL)
105     {
106         assert(0);
107         return NULL;
108     }
109     pNewNode->_pLift = NULL;
110     pNewNode->_pRight = NULL;
111     pNewNode->data = data;
112     return pNewNode;
113 }
114 void PreBTNode(BTNode * pRoot)//先序遍历
115 {
116     if (pRoot)
117     {
118         printf("%c", pRoot->data);
119         PreBTNode(pRoot->_pLift);
120         PreBTNode(pRoot->_pRight);
121     }
122 }
123 void InBTNode(BTNode * pRoot)//中序遍历
124 {
125     if (pRoot)
126     {
127         InBTNode(pRoot->_pLift);
128         printf("%c", pRoot->data);
129         InBTNode(pRoot->_pRight);
130     }
131 }
132 void PostBTNode(BTNode *pRoot)//后序遍历
133 {
134     if (pRoot)
135     {
136         PostBTNode(pRoot->_pLift);
137         PostBTNode(pRoot->_pRight);
138         printf("%c", pRoot->data);
139     }
140 }
141 //test.c
142 #include"BTree.h"
143 void Test()
144 {
145     char *str = "ABD###CE##F";
146     BTNode *pRoot = NULL;
147     BTNode *pRootC = NULL;
148     int index = 0;
149     CreatBinTree(&pRoot, str, strlen(str), &index,'#');//创建二叉树
150     printf("前序遍历：");
151     PreBTNode(pRoot);
152     printf("
");
153     printf("中序遍历：");
154     InBTNode(pRoot);
155     printf("
");
156     printf("后序遍历：");
157     PostBTNode(pRoot);
158     printf("
");
159     pRootC = CopyBinTree(pRoot);
160     printf("前序遍历：");
161     PreBTNode(pRootC);
162     printf("
");
163     printf("中序遍历：");
164     InBTNode(pRootC);
165     printf("
");
166     printf("后序遍历：");
167     PostBTNode(pRootC);
168     printf("
");
169     printf("二叉树中节点的总个数：");
170     printf("%d ", GetBTNodeCount(pRoot));
171     printf("
");
172     printf("二叉树中叶子节点的个数：");
173     printf("%d ", GetLeafBTnodCount(pRoot));
174     printf("
");
175     printf("二叉树中第3层中节点的个数：");
176     printf("%d", GetKLevelBTNodCount(pRoot, 3));
177     printf("
");
178     printf("二叉树的高度：");
179     printf("%d ", HeightBTree(pRoot));
180     DestoryBinTree(&pRoot);
181     DestoryBinTree(&pRootC);
182 }
183 
184 int main()
185 {
186     Test();
187     system("pause");
188     return 0;
189 }
190 //BTNode.h:
191 #pragma once
192 #include<stdio.h>
193 #include<stdlib.h>
194 #include<assert.h>
195 
196 typedef int BDataType;
197 typedef struct BTNode
198 {
199     struct BTNode *_pLift;
200     struct BTNode *_pRight;
201     BDataType data;
202 }BTNode;
203 
204 void CreatBinTree(BTNode **pRoot, char *str, int size, int *index,BDataType invalid);//创建二叉树
205 void PreBTNode(BTNode * pRoot);//先序遍历
206 void InBTNode(BTNode * pRoot);//中序遍历
207 void PostBTNode(BTNode *pRoot);//后序遍历
208 BTNode *BuyNewNode(BDataType data);//购买新节点
209 BTNode *CopyBinTree(BTNode *pRoot);//拷贝新节点
210 void DestoryBinTree(BTNode **pRoot);//销毁二叉树
211 int GetBTNodeCount(BTNode *pRoot);//获取二叉树的结点个数
212 int GetLeafBTnodCount(BTNode *pRoot);//获取叶子节点的个数
213 int GetKLevelBTNodCount(BTNode *pRoot,int k);//获取第K层节点的个数
214 int HeightBTree(BTNode *pRoot);//获取二叉树的高度
215 BTNode * LeftChild(BTNode *pRoot);//获取左右孩子
216 BTNode * RightChild(BTNode *pRoot);

相关阅读:
uml 类图
 Java IO流
 Spring 创建Bean的三种方式
 linux+jmeter+python基础+抓包拦截
 接口测试
 HDU 1159 Common Subsequence(POJ 1458)
HDU 1160 FatMouse's Speed
HDU 4540 威威猫系列故事——打地鼠
 HDU 1087 Super Jumping! Jumping! Jumping!
HDU 1176 免费馅饼
原文地址：https://www.cnblogs.com/love-you1314/p/9755213.html