本文来自于对邓俊辉老师编著《数据结构(C++语言版)(第3版)》和网上大神们的博客整理而来。
博客中有个人理解,而个人水平有限,故若有错误的地方,请留言指出,谢谢!
一、哈希表
1、哈希表的定义
哈希表(hash table,也称散列表),是根据关键码值(Key value)而直接进行访问的数据结构(循值访问 call by value)。它通过把关键码值映射到表中的一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
散列表的基本构思,可概括为:开辟物理地址连续的桶数组ht[ ],借助散列函数hash(),将词条关键码key映射为桶地址hash(key),从而快速地确定待操作词条的物理位置。
2、散列函数(哈希函数)
数组寻址容易,链表插入和删除容易,哈希表则具有两者的优势。而为克服哈希表在存储空间利用率上的不足,我们首先要了解散列函数的设计。
2.1 设计原则:
a)必须具有确定性。无论数据项如何,词条E在散列表中的映射地址hash(E.key) 必须完全取决于其关键码E.key;
b)映射过程不能复杂,唯此方能保证散列地址的计算可快速完成;
c)所有关键码经映射后尽量覆盖整个地址空间,唯有此方可充分利用有限的散列表空间。即,函数hash()最好是满射。
关键码不同的词条被映射到同一散列地址的情况称为散列冲突。(这难以彻底避免,词条多,散列地址少)
为尽可能的降低冲突发生的概率,最为重要的一条原则是,关键码映射到各桶的概率尽量接近1/M,M为散列表长。总而言之,随机越强,规律越弱的散列函数越好。
3 哈希函数构造方法
3.1 除余法(division method)
就是将散列表(哈希表)长度M取为素数(很重要),并将关键码key映射至key关于M整除的余数:
hash(key)= key % M
如已知待散列元素为(18,90,43,54),M=7,则对应的hash(key)的值分别为(4,6,1,5).
注:采取除余法时,必须将M选作素数,否则关键码被映射到[0,M)范围内的均匀度将大幅降低,发生冲突的概率将随着M所含素因子的增多而迅速加大。若词条关键码间隔T个数足够大而且恰好可被M整除,则所有被访问的词条都将相互冲突,如(100,120,140,160,180.....)以等差数列的形式出现时,M为20,则hash(key)=0。
另外,若M不为素数,则使用除余法时,应为key % p ,其中p为小于M的最大素数。
拓展:
上面相邻关键码所对应的散列对峙,总是彼此相邻,即依然残留某种连续性。可采用MAD法(multiply-and-divide method):
关键码的映射为:(a×key+b) % M ,其中M仍为素数,a>0,b>0,且a % M≠0 。除余法是当a=1,b=0时的特殊情况。
3.2 更多散列函数
(1)数字分析法 (selecting digits)
从关键码key特定进制的展开中抽取特定的若干位,构成一个整型地址。若,从十进制展开中的奇数位,则由hash(123456789) =1357.
(2)平方取中法(mid-square)
从关键码key的平方的十进制或二进制展开中取居中的若干位,构成一个整型地址。
若取平方后十进制展开中居中的三位,则有hash(123) = 15129 =512
(3)折叠法(folding)
将关键码的十进制或二进制展开分割成等宽的若干段,取其总和作为散列地址。如:以三个数为分割单位,则有 hash(123456789)=123+456+789=1368
另外,折叠法分割后,分割各区段的方向也可以是往复折叠式的,则有hash(123456789)=123+654+987=1566
(4)位异或法(xor)
将关键码的二进制展开分割成等宽的若干段,经异或元素得到散列地址,比如以三个数位为分割单位,则有hash(110011011b)=110^011^011=110b=6
同样分割各区段的方向也可以是往复折返式的。
注:为保证上述函数取值落在合法的散列地址空间以内,通常都还需要对散列表长度M再做一次取余运算。
3.3(伪)随机数法
散列函数越是随机、越是没有规律、就越是好的散列函数,按照这一标准,任何一个(伪)随机数发生器,本身即时一个好的散列函数,比如可直接使用C++语言提供的rand()函数,将关键码key映射到桶地址:
rand(key) % M ,其中rand(key)为系统定义的第key个(伪)随机数。
特别值得注意的是,由于不同计算环境所提供的(伪)随机发生器不尽相同,故在将某一系统中生成的散列表移植到另一系统时,必须格外小心。
二、冲突及其排解
1、多槽位(multiple slots)法
将彼此冲突的每一组词条组织为一个小小规模的子词典,分别存放于他们共同对应的桶单元中。比如一种简便的方法是,统一将各桶细分为更小的称作为操作(slot)的若干单元,每一组槽位可组织为向量或列表。如下图:
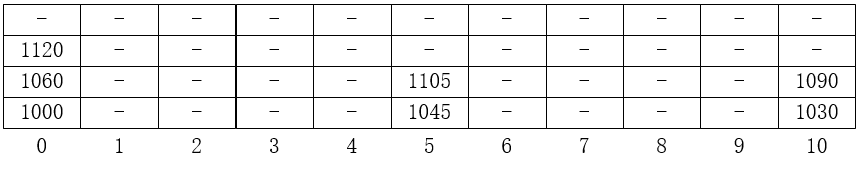
将每个桶分成4个槽位。只要相互冲突的各族关键码不超过4个,即可分别保存于对应的桶单元内的不同槽位。
缺点:绝大多数的槽位通常都处于空闲状态。另外,关于槽位细分成何种程度,方可保证在任何情况下都能够用,很难确定。有时,甚至会出现几乎其余所有的桶都是处于空闲状态,而某个桶却会因为冲突过多而溢出。
2、独立链(separate chaining)法
与多槽位法类似,也令相互冲突的每个词条构成小规模的子词典,只不过采用列表(而非向量)来实现各子词典。
个人理解书上的独立链法和网上所说的链地址法是同一方法。
当关键字为{32,40,36,16,46,71,27,42,24,49,64},哈希表的长度M=13,哈希函数为hash(key)= key % M,结果如下图:
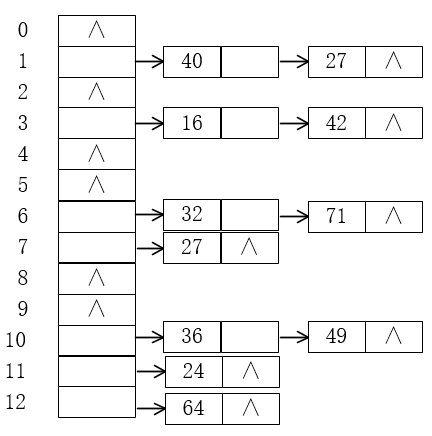
有效的降低了空间消耗,但在查找过程中一旦发生冲突,则需要遍历相应的整个链表,导致查找成本的增加。
3、公共溢出区法
基本思想是:将哈希表分为基本表和溢出表两部分,一旦插入词条和基本表中发生冲突,转存到溢出表中。
4、闭散列策略(亦称作开放定址(open addressing))
尽管就逻辑结构而言,独立链等策略便捷而紧凑,但绝非上策。实际上,仅仅一开基本的散列表结构,且就地排解冲突,反而是更好的选择。也就是说,若新词条与已有词条冲突,则只允许在散列表内部为其寻找另一个空桶。如此,各桶并非注定只能存放特定的一个词条,从理论上讲,每个桶单元都有可能存放一个词条。
(1)线性试探法
在插入关键码key时,若发现桶单元ht[hash(key)]已被占用,则转而试探桶单元he[hash(key)+1],若桶单元he[hash(key)+1]也被占用,则继续试探he[hash(key)+2],如此不断,知道发现一个空桶。为保证桶地址的合法,最后还需同一对M取模。因此,第i次试探的桶单元应为:
ht[ (hash(key)+i) % M] ,i=1,2,3,.....
如此,被试探的桶单元在物理空间上一次连贯,其地址构成等差数列,该方法由此得名。
(2)平方试探法
若在查找过程若连续发生冲突,则按如下规则确定第j次试探桶地址:
(hash (key) +j2 ) % M ,j=0,1,2.....
各次试探的位置到起始位置的距离,以平方速率增长,该方法因此得名。
(3)(伪)随机试探(pseudo-random probing)法
借助(伪)随机数发生器来确定试探位置,具体,第j次试探的桶地址取作:
rand( j ) % M (rand( j )为系统定义的第j个(伪)随机数) 跨平台慎用!
(4)再散列(double hashing)法
选取一个适宜的二级散列函数hash2( ),一旦插入词条(key ,value)时发现ht[hash(key)]已被占用,则以hash2(key)为偏移增量继续尝试,直到发现一个空桶。如此被尝试的桶地址依次应为:
[hash(key) +1×hash2(key) ] % M
[hash(key) +2×hash2(key) ] % M
[hash(key) +3×hash2(key) ] % M
..................
可见,再散列法是对此前各方法的概括。比如取hash2(key)=1时即线性试探法。
同类解释链接:
http://www.360doc.com/content/14/0721/09/16319846_395862328.shtml#