基本排序之归并排序

归并排序：

概述：归并排序就是讲数组不断分为左右各半的数组，然后通过整体外排，就是小数组排好序之后，合并起来，用一个大数组来保存合并的之后的元素。

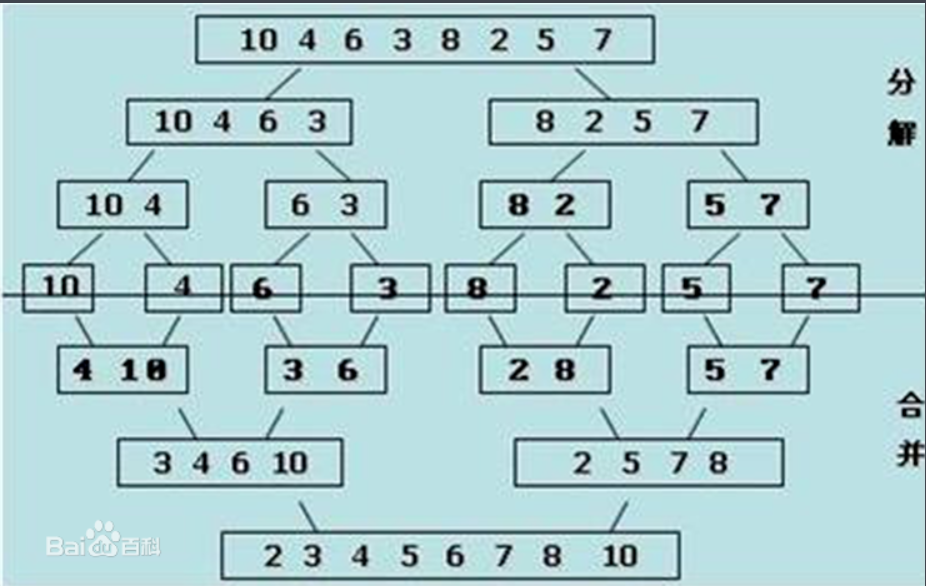
（1）通过二分法，不断的将原数组分为左边两半的数组。一直二分，直到划分到不能继续二分为止，即只有一个元素。

（2）进行合并。

（3）申请辅助空间，长度为R-L+1。将小数组比较大小，从小到大保存在辅助数组里面。

（4）然后把辅助数组里面的元素依次赋值给原数组中对应的位置。

时间复杂度：

　　O(NlogN)。但所需空间复杂度为O(N)，因为要申请一个大数组。

稳定性：

　　稳定算法。

代码如下：

#include <iostream>
#include <vector>
#include <random>
using namespace std;
//归并并不是真正划分了，只是“脑补”出这种原型
class MergeSort_
{
public:
    void MergeSort(vector<int> &v);
    void MergeSort(vector<int> &v, int L, int R);
    void Merge(vector<int> &v, int L, int M, int R);
};

void MergeSort_::MergeSort(vector<int> &v)
{
    //如果vector为空或者只有一个元素，那么直接返回
    if (v.size() < 2)
        return ;
    //进入归并排序
    MergeSort(v, 0, v.size() - 1);
}
void MergeSort_::MergeSort(vector<int> &v, int L, int R)
{
    if (L == R)
        return;
    int mid = L + ((R - L) >> 1);     //防溢出，右移一位就是除以2.用L加上R，L的距离的一半表示中点
    //进行归并
    MergeSort(v, L,mid);
    MergeSort(v, mid + 1, R);
    Merge(v, L, mid, R);
}

void MergeSort_::Merge(vector<int> &v, int L, int M, int R)
{
    vector<int> vtemp(R-L+1);
    int i = 0;
    int pLeft = L;
    int pRight = M + 1;
    while (pLeft <= M && pRight <= R)
    {
        //把小的值赋值给辅助数组，并继续进行下标偏移
        vtemp[i++] = v[pLeft] < v[pRight] ? v[pLeft++] : v[pRight++];
    }
    //剩下的数直接赋值到vtemp里面
    while (pLeft <= M)
    {
        vtemp[i++] = v[pLeft++];
    }
    while (pRight <= R)
    {
        vtemp[i++] = v[pRight++];
    }
    //最后把辅助数组里面的元素放到原数组中去
    for (size_t i = 0; i < vtemp.size(); i++)
    {
        v[L + i] = vtemp[i];
    }
}

//for test
int main()
{
    MergeSort_ M;
    static default_random_engine e;
    static uniform_int_distribution<int> u(-88,100);
    vector<int> v(10);
    for (int i = 0, j = 9; i < 10; i++,j--)
    {
        v[i]=u(e);
    }
    M.MergeSort(v);
    for (int i = 0; i < 10; i++)
    {
        cout << v[i] << " ";
    }
    return 0;
}