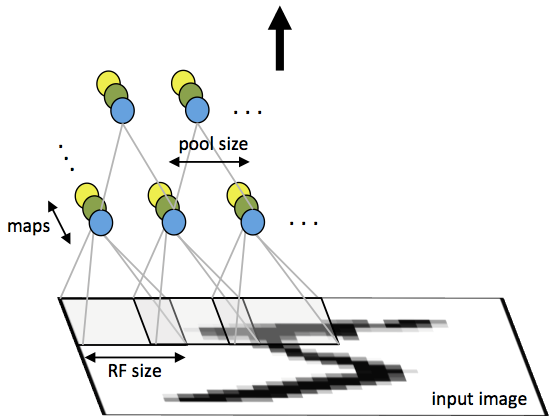
在上篇中介绍的输入层与隐含层的连接称为全连接，如果输入数据是小块图像，比如8×8，那这种方法是可行的，但是如果输入图像是96×96，假设隐含层神经元100个，那么就有一百万个（96×96×100）参数需要学习，向前或向后传播计算时计算时间也会慢很多。
解决这类问题的一种简单方法是对隐含单元和输入单元间的连接加以限制：每个隐含单元仅仅只能连接输入单元的一部分。例如，每个隐含单元仅仅连接输入图像的一小片相邻区域。这也是卷积神经网络的基本思想，它是一种特殊的MLP,这个概念是从生物里面演化过来的. 根据Hubel和Wiesel早期在猫的视觉皮层上的工作, 我们知道在视觉皮层上面存在一种细胞的复杂分布,这些细胞对一些局部输入是很敏感的,它们被成为感知野, 并通过这种特殊的组合方式来覆盖整个视野. 这些过滤器对输入空间是局部敏感的,因此能够更好得发觉自然图像中不同物体的空间相关性。
对一副图片的局部特性的提取在整个视野上是可重复的，比如我们在96×96图像中选取8×8作为样本，在样本上学习到的特征应用到整幅图像上，即利用8×8中学习到的特征在96×96图像上做卷积，从而获得不同的特征值，所需要学习的参数也从96×96降到了8×8，这样成为一个特征图。我们需要从一副图像上学习的特征肯定不止一种，所以需要建立n个特征图来学习不同的特征。即使是这样，算法的复杂度也比之前全连接的方法大大的降低了。
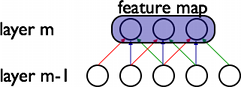
上图即一个特征图的三个隐藏神经元对m-1层输入做卷积，其中共享三个w参数。
卷积神经网络的另外一个步骤是池化(pooling)，它把输入图像分割成不重叠的矩形，对于每个矩形取最大值(max pooling)，另外一种池化方法叫做(mean pooling)，它对每个矩形取平均值。
池化的优势是（1）它降低了上层的计算复杂度 （2）它提供了一种变换不变量的。对于第二种益处，我们可以假设把一个池化层和一个卷积层组合起来，对于单个像素，输入图像可以有8个方向的变换。如果共有最大层在2*2的窗口上面实现，这8个可能的配置中，有3个可以准确的产生和卷积层相同的结果。如果窗口变成3*3，则产生精确结果的概率变成5/8.可见，池化对位置信息提供了附加的鲁棒性，它以一种非常聪明的方式减少了中间表示的维度。下图就是简单的池化过程，右侧矩阵的每个值是左侧每个红色矩阵中元素的最大值（或平均值）。
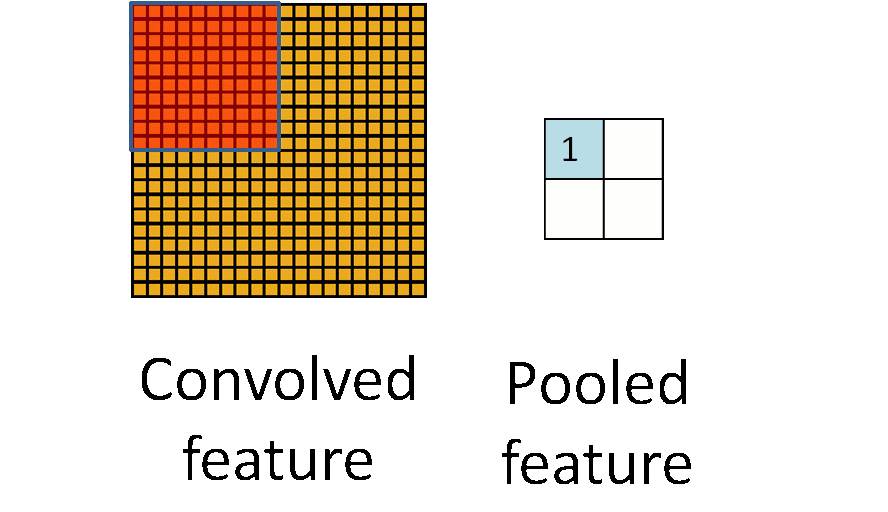
下图是卷积层和池化层的结合，相同颜色的神经元共享权重。
卷积神经网络的训练过程与全联通神经网络类似，首先随机初始化参数，再利用向后传导算法来训练参数。CNN反向传播求导时的具体过程可以参考论文Notes on Convolutional Neural Networks, Jake Bouvrie，该论文讲得很全面。
下面是tornadomeet的博客中对CNN反向传播过程的介绍，很通俗易懂。
问题二：当接在卷积层的下一层为pooling层时，求卷积层的误差敏感项。
假设第l(小写的l，不要看成数字'1'了)层为卷积层，第l+1层为pooling层，且pooling层的误差敏感项为：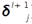 
,卷积层的误差敏感项为：
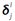, 则两者的关系表达式为：
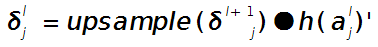
这里符号●表示的是矩阵的点积操作，即对应元素的乘积。卷积层和unsample()后的pooling层节点是一一对应的，所以下标都是用j表示。后面的符号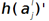
表示的是第l层第j个节点处激发函数的导数(对节点输入的导数)。
其中的函数unsample()为上采样过程，其具体的操作得看是采用的什么pooling方法了。但unsample的大概思想为：pooling层的每个节点是由卷积层中多个节点(一般为一个矩形区域)共同计算得到，所以pooling层每个节点的误差敏感值也是由卷积层中多个节点的误差敏感值共同产生的，只需满足两层见各自的误差敏感值相等，下面以mean-pooling和max-pooling为例来说明。
假设卷积层的矩形大小为4×4, pooling区域大小为2×2, 很容易知道pooling后得到的矩形大小也为2*2（本文默认pooling过程是没有重叠的，卷积过程是每次移动一个像素，即是有重叠的，后续不再声明）,如果此时pooling后的矩形误差敏感值如下：
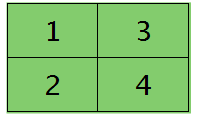
则按照mean-pooling，首先得到的卷积层应该是4×4大小，其值分布为(等值复制)：
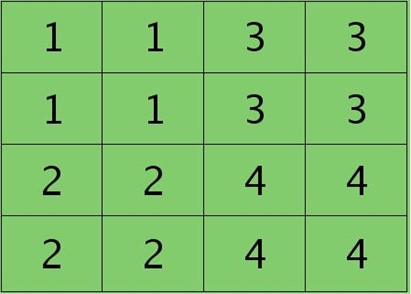
因为得满足反向传播时各层见误差敏感总和不变，所以卷积层对应每个值需要平摊（除以pooling区域大小即可，这里pooling层大小为2×2=4)），最后的卷积层值
分布为：
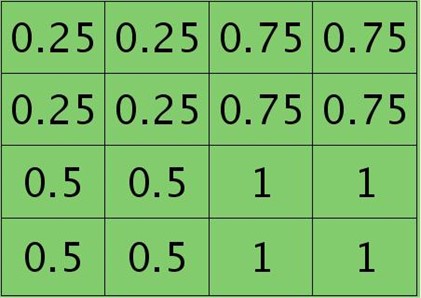
mean-pooling时的unsample操作可以使用matalb中的函数kron()来实现，因为是采用的矩阵Kronecker乘积。C=kron(A, B)表示的是矩阵B分别与矩阵A中每个元素相乘，然后将相乘的结果放在C中对应的位置。比如：
如果是max-pooling，则需要记录前向传播过程中pooling区域中最大值的位置，这里假设pooling层值1,3,2,4对应的pooling区域位置分别为右下、右上、左上、左下。则此时对应卷积层误差敏感值分布为：
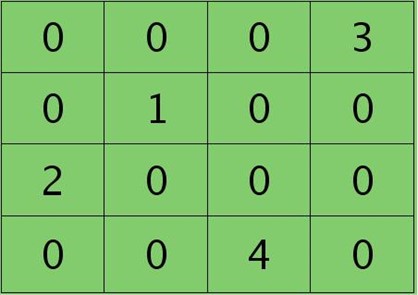
当然了，上面2种结果还需要点乘卷积层激发函数对应位置的导数值了，这里省略掉。
问题三：当接在pooling层的下一层为卷积层时，求该pooling层的误差敏感项。
假设第l层(pooling层)有N个通道，即有N张特征图，第l+1层(卷积层)有M个特征，l层中每个通道图都对应有自己的误差敏感值，其计算依据为第l+1层所有特征核的贡献之和。下面是第l+1层中第j个核对第l层第i个通道的误差敏感值计算方法：
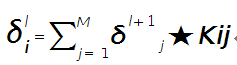
符号★表示的是矩阵的卷积操作，这是真正意义上的离散卷积，不同于卷积层前向传播时的相关操作，因为严格意义上来讲，卷积神经网络中的卷积操作本质是一个相关操作，并不是卷积操作，只不过它可以用卷积的方法去实现才这样叫。而求第i个通道的误差敏感项时需要将l+1层的所有核都计算一遍，然后求和。另外因为这里默认pooling层是线性激发函数，所以后面没有乘相应节点的导数。
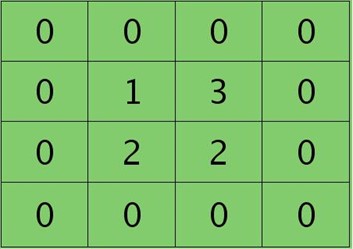
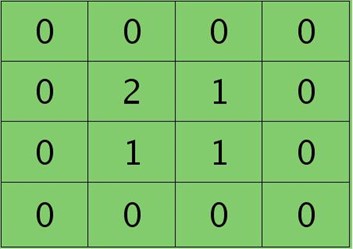
举个简单的例子，假设拿出第l层某个通道图，大小为3×3，第l+1层有2个特征核，核大小为2×2，则在前向传播卷积时第l+1层会有2个大小为2×2的卷积图。如果2个特征核分别为：
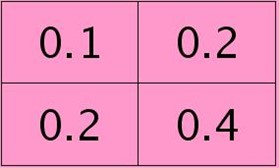
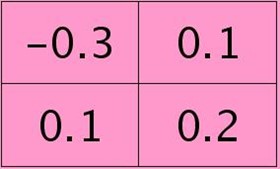
反向传播求误差敏感项时，假设已经知道第l+1层2个卷积图的误差敏感值：
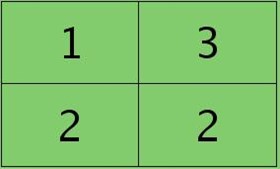
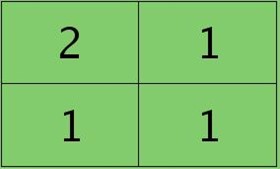
离散卷积函数conv2()的实现相关子操作时需先将核旋转180度(即左右翻转后上下翻转)，但这里实现的是严格意义上的卷积，所以在用conv2()时，对应的参数核不需要翻转（在有些toolbox里面，求这个问题时用了旋转，那是因为它们已经把所有的卷积核都旋转过，这样在前向传播时的相关操作就不用旋转了。并不矛盾）。且这时候该函数需要采用'full'模式，所以最终得到的矩阵大小为3×3,（其中3=2+2-1）,刚好符第l层通道图的大小。采用'full'模式需先将第l+1层2个卷积图扩充，周围填0,padding后如下：
扩充后的矩阵和对应的核进行卷积的结果如下情况：
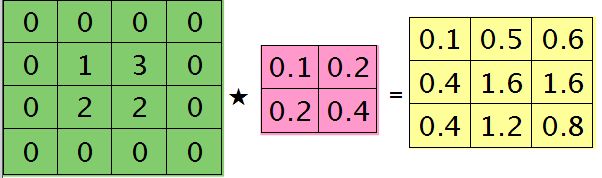
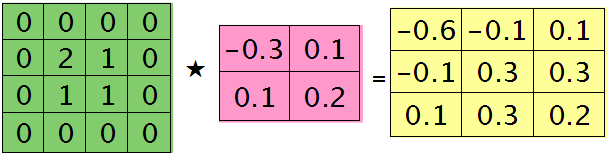
可以通过手动去验证上面的结果，因为是离散卷积操作，而离散卷积等价于将核旋转后再进行相关操作。而第l层那个通道的误差敏感项为上面2者的和，呼应问题三，最终答案为：
那么这样问题3这样解的依据是什么呢？其实很简单，本质上还是bp算法，即第l层的误差敏感值等于第l+1层的误差敏感值乘以两者之间的权值，只不过这里由于是用了卷积，且是有重叠的，l层中某个点会对l+1层中的多个点有影响。比如说最终的结果矩阵中最中间那个0.3是怎么来的呢？在用2×2的核对3×3的输入矩阵进行卷积时，一共进行了4次移动，而3×3矩阵最中间那个值在4次移动中均对输出结果有影响，且4次的影响分别在右下角、左下角、右上角、左上角。所以它的值为2×0.2+1×0.1+1×0.1-1×0.3=0.3, 建议大家用笔去算一下，那样就可以明白为什么这里可以采用带'full'类型的conv2()实现。
问题四：求与卷积层相连那层的权值、偏置值导数。
前面3个问题分别求得了输出层的误差敏感值、从pooling层推断出卷积层的误差敏感值、从卷积层推断出pooling层的误差敏感值。下面需要利用这些误差敏感值模型中参数的导数。这里没有考虑pooling层的非线性激发，因此pooling层前面是没有权值的，也就没有所谓的权值的导数了。现在将主要精力放在卷积层前面权值的求导上(也就是问题四)。
假设现在需要求第l层的第i个通道，与第l+1层的第j个通道之间的权值和偏置的导数，则计算公式如下：
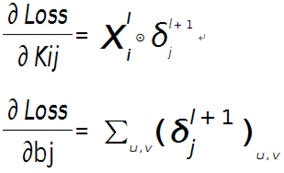
其中符号⊙表示矩阵的相关操作，可以采用conv2()函数实现。在使用该函数时，需将第l+1层第j个误差敏感值翻转。
例如，如果第l层某个通道矩阵i大小为4×4,如下：
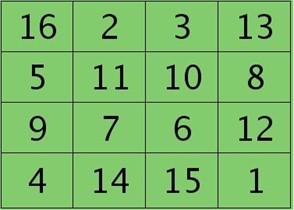
第l+1层第j个特征的误差敏感值矩阵大小为3×3,如下：
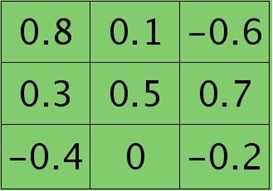
很明显，这时候的特征Kij导数的大小为2×2的，且其结果为：
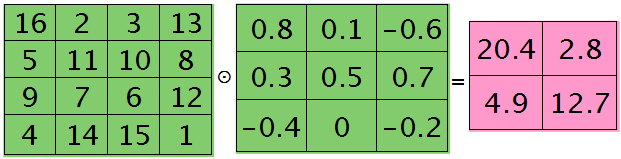
而此时偏置值bj的导数为1.2 ，将j区域的误差敏感值相加即可(0.8+0.1-0.6+0.3+0.5+0.7-0.4-0.2=1.2)，因为b对j中的每个节点都有贡献，按照多项式的求导规则(和的导数等于导数的和)很容易得到。
为什么采用矩阵的相关操作就可以实现这个功能呢？由bp算法可知，l层i和l+1层j之间的权值等于l+1层j处误差敏感值乘以l层i处的输入，而j中某个节点因为是由i+1中一个区域与权值卷积后所得，所以j处该节点的误差敏感值对权值中所有元素都有贡献，由此可见，将j中每个元素对权值的贡献(尺寸和核大小相同)相加，就得到了权值的偏导数了(这个例子的结果是由9个2×2大小的矩阵之和)，同样，如果大家动笔去推算一下，就会明白这时候为什么可以用带'valid'的conv2()完成此功能。
池化矩阵一般为2×2，对于非常大的图像可能会使用4×4，但取值时要谨慎，这可能会损失掉太多的输入信息。
由于特征图中神经元的数量会随着层数的深入而减小，靠近输入层的特征图数量应该更多点来平衡每一层的计算量，为了不使输入信息丢失，应该使每一层的激活值数量（特征图数量乘以像素值）一致，特征图数量大小取决于算法的复杂度，数量太多会使得计算复杂度大幅上升。